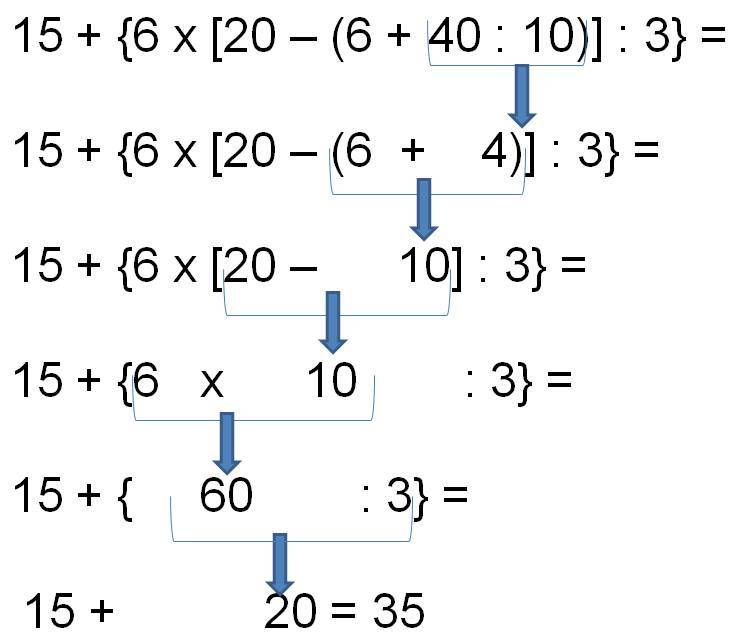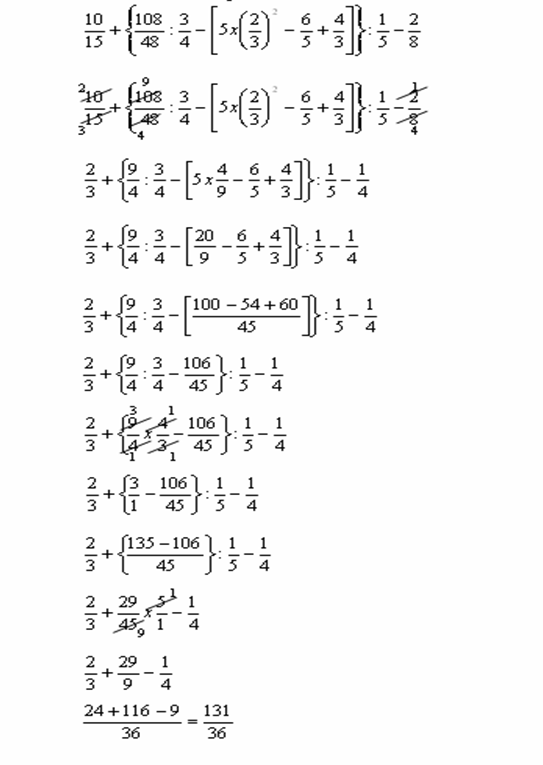Espressioni Seconda Media Con Soluzioni

Ciao a tutti ragazzi di seconda media! Siete pronti ad affrontare il fantastico mondo delle espressioni matematiche? So che a volte possono sembrare un po' ostiche, un vero rompicapo, ma non preoccupatevi, sono qui per aiutarvi a superare ogni difficoltà! Ho preparato per voi una guida super dettagliata, ricca di trucchi e consigli utili, e soprattutto, un sacco di espressioni con le soluzioni. Insieme, le sviscereremo passo dopo passo, trasformando le vostre paure in pura soddisfazione. Forza, cominciamo subito!

Innanzitutto, è fondamentale avere ben chiare le regole delle precedenze. Sembra banale, lo so, ma è la base di tutto! Prima di ogni altra cosa, dobbiamo occuparci delle parentesi: prima quelle tonde ( ), poi le quadre [ ], e infine le graffe { }. All'interno di ogni parentesi, l'ordine da seguire è: potenze, moltiplicazioni e divisioni (nell'ordine in cui compaiono, da sinistra verso destra), e infine addizioni e sottrazioni (anche qui, nell'ordine in cui compaiono). Ricordatevi questa scaletta, perché sarà la vostra bussola nel mare delle espressioni!

Per quanto riguarda le frazioni, non abbiate timore! Semplicemente, trattatele come delle divisioni. Se trovate una frazione all'interno di una parentesi, calcolatela come fareste normalmente con una divisione. E se avete somme o sottrazioni tra frazioni, ricordatevi di trovare il minimo comune denominatore (m.c.d.). So che può sembrare complicato all'inizio, ma con un po' di pratica diventerà automatico!

Passiamo ora ad alcune espressioni di esempio. Preparate carta e penna, perché le risolveremo insieme!

Esempio 1:

2 + 3 x (5 - 1) + 4 : 2

1. Parentesi: 5 - 1 = 4
2. Moltiplicazione: 3 x 4 = 12
3. Divisione: 4 : 2 = 2
4. Addizioni: 2 + 12 + 2 = 16

Quindi, il risultato finale è 16! Facile, vero?

Esempio 2:

[ ( 7 + 3 ) : 2 - 1 ] x 5

1. Parentesi tonda: 7 + 3 = 10
2. Divisione nella parentesi quadra: 10 : 2 = 5
3. Sottrazione nella parentesi quadra: 5 - 1 = 4
4. Moltiplicazione: 4 x 5 = 20

Il risultato è 20! Avete visto come, seguendo l'ordine corretto, anche un'espressione apparentemente complessa si semplifica notevolmente?

Esempio 3 (con frazioni):

(1/2 + 1/4) x 8 - 3/2

1. Parentesi: Troviamo il m.c.d. tra 2 e 4, che è 4. Quindi, 1/2 = 2/4. L'espressione diventa (2/4 + 1/4) x 8 - 3/2.
2. Somma nella parentesi: 2/4 + 1/4 = 3/4
3. Moltiplicazione: 3/4 x 8 = 24/4 = 6
4. Sottrazione: 6 - 3/2. Troviamo il m.c.d. tra 1 (il denominatore di 6, che è come dire 6/1) e 2, che è 2. Quindi, 6 = 12/2. L'espressione diventa 12/2 - 3/2 = 9/2

Il risultato finale è 9/2! Non abbiate paura delle frazioni, sono solo numeri come gli altri!

Esempio 4 (con potenze):

5^2 - (2 x 3 + 1) + 2^3 : 4

1. Potenze: 5^2 = 25 e 2^3 = 8
2. Parentesi: 2 x 3 = 6, poi 6 + 1 = 7
3. Divisione: 8 : 4 = 2
4. Sottrazione e addizione: 25 - 7 + 2 = 20

Il risultato è 20! Ricordatevi sempre di calcolare le potenze prima di moltiplicazioni e divisioni.

Consigli extra per diventare dei veri maghi delle espressioni

Oltre a conoscere le regole, ci sono alcuni trucchetti che possono aiutarvi a risolvere le espressioni in modo più rapido ed efficiente.

• Scrivete in modo ordinato: Sembra una sciocchezza, ma scrivere le espressioni in modo chiaro e ordinato vi aiuterà a non commettere errori. Utilizzate un foglio a quadretti e allineate bene i numeri.
• Controllate sempre i segni: Un segno sbagliato può compromettere l'intero risultato. Prestate particolare attenzione ai segni meno, soprattutto quando sono davanti a una parentesi.
• Semplificate le frazioni: Prima di iniziare a calcolare, cercate di semplificare le frazioni riducendole ai minimi termini. Questo vi semplificherà i calcoli successivi.
• Utilizzate le proprietà delle operazioni: Ad esempio, la proprietà distributiva della moltiplicazione rispetto all'addizione può essere molto utile per semplificare le espressioni.
• Esercitatevi, esercitatevi, esercitatevi! Non c'è modo migliore per imparare che fare tanta pratica. Più espressioni risolverete, più diventerete bravi e veloci.

Espressioni con soluzioni per allenarvi

Ed ecco una serie di espressioni con le soluzioni per mettervi alla prova. Non abbiate paura di sbagliare, l'importante è imparare dai propri errori!

1. (4 + 2 x 3) - 5 = 5
2. 12 : (6 - 2) + 1 = 4
3. [15 - (3 + 4) x 2] + 7 = 8
4. (1/3 + 1/6) x 12 - 2 = 4
5. 3^2 + (10 - 4 x 2) - 1 = 10
6. {2 + [3 x (5 - 2) - 4] } : 3 = 3
7. (5/2 - 1/4) x 4 + 1/2 = 9/2
8. 4^2 - (2 x 5 + 3) + 3^2 : 3 = 6
9. [ ( 8 + 2 ) : 5 + 1 ] x 2 - 1 = 5
10. (1/2 + 3/4) : 5/8 - 1/5 = 3/5
11. 25 : 5 + 3 x ( 8 - 6 ) - 1 = 10
12. [ 16 - ( 2 + 3 ) x 2 ] + 4 : 2 = 8
13. ( 2/3 + 1/6 ) x 9 - 4/5 = 27/10
14. 4^2 - ( 3 x 2 + 4 ) + 2^3 : 2 = 10
15. { 1 + [ 2 x ( 6 - 3 ) - 2 ] } : 5 = 1

Controllate le vostre soluzioni con quelle che vi ho fornito. Se avete sbagliato, cercate di capire dove avete commesso l'errore e riprovate. Non arrendetevi!

Spero che questa guida vi sia stata utile. Ricordatevi, la matematica è un gioco, un puzzle da risolvere. Con un po' di impegno e tanta curiosità, potrete diventare dei veri esperti! In bocca al lupo per il vostro percorso matematico! E se avete bisogno di altro aiuto, non esitate a chiedere! Sono qui per voi!