Dominio Di Una Funzione Definizione

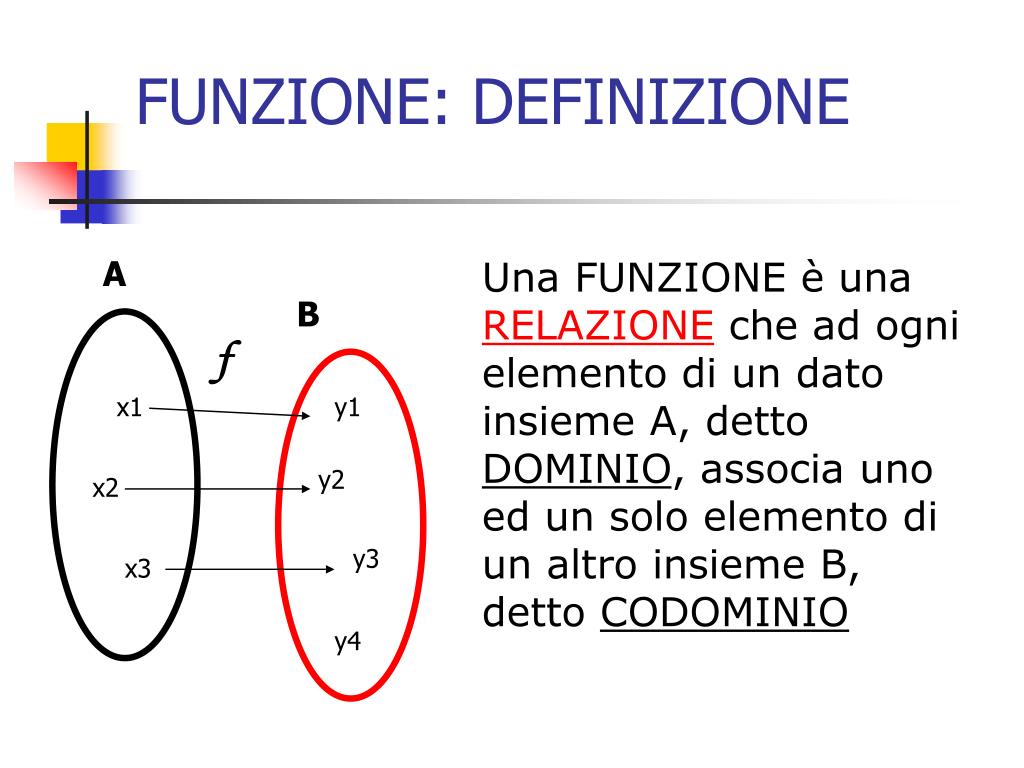
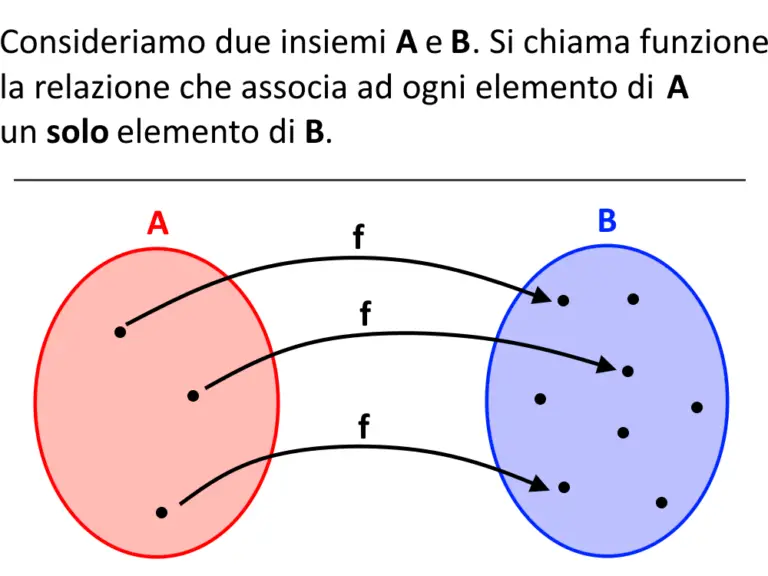
In un universo di relazioni matematiche, la funzione si erge come un'entità fondamentale, un legame imprescindibile tra due insiemi di valori. Per comprendere appieno la natura e l'operato di una funzione, è essenziale volgere la nostra attenzione a un concetto cardine: il suo dominio.

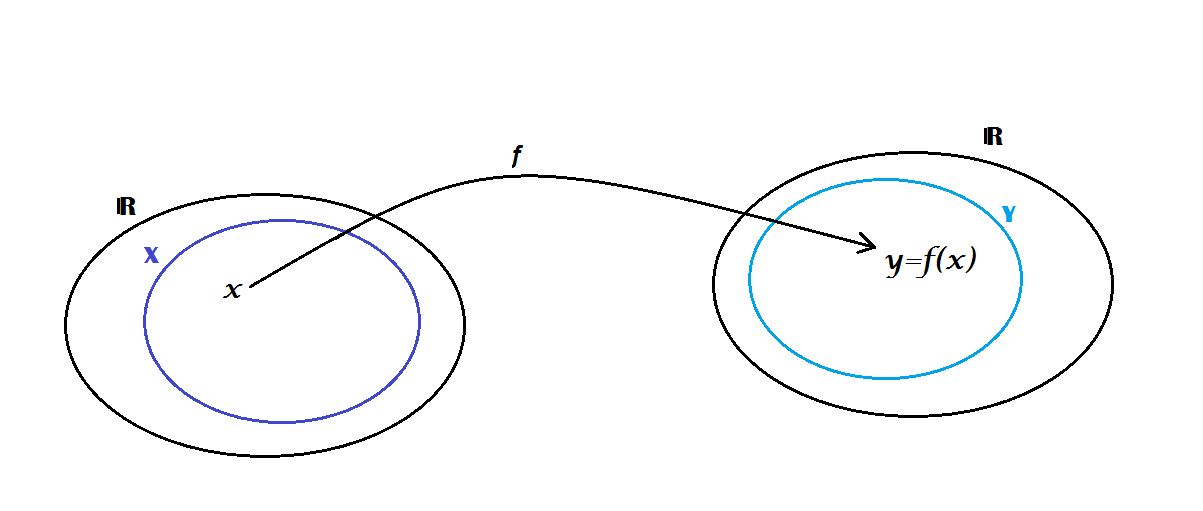
Il dominio di una funzione, in termini rigorosi e precisi, è l'insieme di tutti i valori che la variabile indipendente (solitamente indicata con la lettera 'x') può assumere, affinché la funzione stessa produca un valore reale e definito. In altre parole, il dominio rappresenta la totalità degli input possibili per la funzione, quelli che non la conducono a risultati indefiniti, inesistenti o non reali.

Immaginiamo una macchina complessa, in cui inseriamo degli ingredienti (i valori di 'x') per ottenere un prodotto finale (il valore della funzione, solitamente indicato con 'y' o f(x)). Il dominio rappresenta l'elenco degli ingredienti ammissibili per quella specifica macchina; se inseriamo un ingrediente non appropriato, la macchina potrebbe bloccarsi, produrre un risultato errato o addirittura danneggiarsi.

La determinazione del dominio di una funzione è un'operazione di cruciale importanza nell'analisi matematica. Essa ci permette di definire con esattezza l'ambito di validità della funzione, di identificare eventuali restrizioni o limitazioni nel suo utilizzo e di evitare errori grossolani nell'interpretazione dei risultati.

Consideriamo ora alcune tipologie comuni di funzioni e le relative considerazioni sul dominio:

Funzioni polinomiali: Queste funzioni, espresse come somme di termini in cui la variabile 'x' è elevata a potenze intere non negative (ad esempio, f(x) = 3x² + 2x - 1), possiedono il dominio più ampio e incondizionato possibile. In altre parole, qualsiasi valore reale può essere sostituito al posto di 'x', senza incorrere in problemi di definizione. Il dominio di una funzione polinomiale è, pertanto, l'insieme di tutti i numeri reali, indicato con il simbolo R o con la notazione (-∞, +∞).
Funzioni razionali: Le funzioni razionali sono espresse come quozienti di due polinomi (ad esempio, f(x) = (x + 1) / (x - 2)). In questo caso, il dominio è limitato dalla condizione che il denominatore non possa mai essere uguale a zero. Se il denominatore si annulla per uno o più valori di 'x', questi valori devono essere esclusi dal dominio, poiché la divisione per zero è un'operazione non definita. Per trovare il dominio, è quindi necessario risolvere l'equazione "denominatore = 0" e rimuovere le soluzioni dall'insieme dei numeri reali. Nell'esempio citato, il denominatore (x - 2) si annulla quando x = 2. Pertanto, il dominio della funzione è l'insieme di tutti i numeri reali eccetto il 2, che può essere espresso come R \ {2} o come (-∞, 2) ∪ (2, +∞).
Funzioni irrazionali (con indice pari): Queste funzioni contengono radici di espressioni algebriche, dove l'indice della radice è un numero pari (ad esempio, f(x) = √(x - 3)). In questo contesto, è fondamentale garantire che l'espressione sotto la radice (il radicando) sia sempre maggiore o uguale a zero. Infatti, le radici di indice pari di numeri negativi non sono definite nell'insieme dei numeri reali. Per determinare il dominio, è necessario risolvere la disequazione "radicando ≥ 0". Nell'esempio citato, la disequazione è (x - 3) ≥ 0, la cui soluzione è x ≥ 3. Pertanto, il dominio della funzione è l'insieme di tutti i numeri reali maggiori o uguali a 3, espresso come [3, +∞).
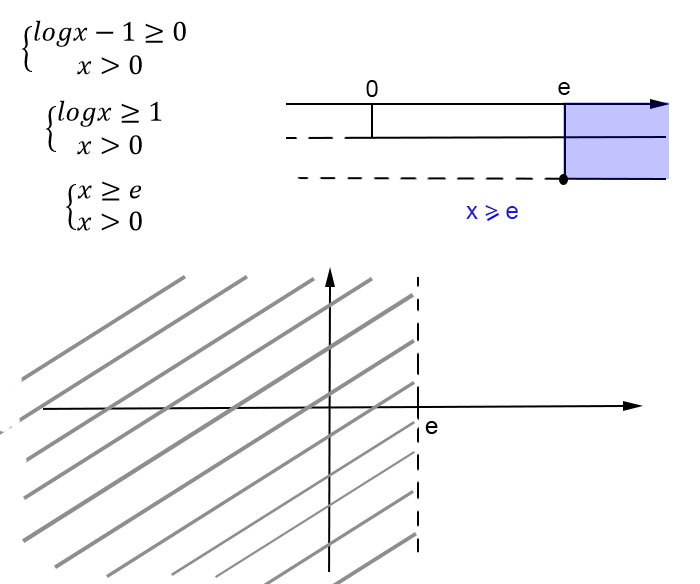
Funzioni logaritmiche: Le funzioni logaritmiche (ad esempio, f(x) = log(x + 4)) sono definite solo per argomenti strettamente positivi. Il logaritmo di un numero non positivo (zero o negativo) non esiste nell'insieme dei numeri reali. Pertanto, per trovare il dominio, è necessario risolvere la disequazione "argomento > 0". Nell'esempio citato, la disequazione è (x + 4) > 0, la cui soluzione è x > -4. Il dominio della funzione è quindi l'insieme di tutti i numeri reali maggiori di -4, espresso come (-4, +∞).
Funzioni trigonometriche: Le funzioni trigonometriche, come seno (sin x) e coseno (cos x), sono definite per tutti i numeri reali, quindi il loro dominio è R. Tuttavia, altre funzioni trigonometriche, come la tangente (tan x = sin x / cos x), presentano delle restrizioni. La tangente non è definita quando il coseno è uguale a zero, ovvero per x = π/2 + kπ, dove k è un numero intero. Pertanto, il dominio della tangente è l'insieme di tutti i numeri reali eccetto i valori per cui cos x = 0. Allo stesso modo, la cotangente (cot x = cos x / sin x) non è definita quando il seno è uguale a zero, ovvero per x = kπ, dove k è un numero intero.

Intersezioni di Domini

In situazioni in cui una funzione è definita come combinazione di diverse sotto-funzioni (ad esempio, una funzione definita a tratti, oppure una funzione che coinvolge radici, logaritmi e quozienti), è necessario determinare il dominio di ciascuna sotto-funzione e, successivamente, trovare l'intersezione di tutti questi domini. L'intersezione rappresenta l'insieme dei valori di 'x' che soddisfano contemporaneamente le condizioni di esistenza di tutte le sotto-funzioni.

Metodi di Determinazione del Dominio

La determinazione del dominio di una funzione richiede un approccio sistematico e rigoroso. È fondamentale identificare tutte le possibili restrizioni (divisioni per zero, radici di indice pari di numeri negativi, logaritmi di numeri non positivi, ecc.) e tradurle in disequazioni o equazioni. La risoluzione di queste equazioni e disequazioni fornisce l'insieme dei valori di 'x' che devono essere esclusi o inclusi nel dominio.

La rappresentazione grafica del dominio può essere un valido strumento per visualizzare e comprendere l'insieme dei valori ammissibili. Possiamo utilizzare la retta reale per evidenziare gli intervalli in cui la funzione è definita e i punti in cui essa non lo è.

Inoltre, è importante ricordare che la determinazione del dominio non è un processo puramente meccanico. Essa richiede una profonda comprensione della natura della funzione, delle sue proprietà e delle sue limitazioni. Un'analisi accurata e consapevole ci permette di evitare errori e di ottenere risultati corretti e significativi.

L'importanza del dominio non si limita alla mera definizione matematica di una funzione; esso influenza profondamente l'interpretazione dei risultati, la risoluzione di problemi e la modellizzazione di fenomeni reali. Un'applicazione appropriata del concetto di dominio ci permette di dare un significato concreto e tangibile alle astrazioni matematiche, rendendo la matematica uno strumento prezioso per la comprensione del mondo che ci circonda. Il dominio, quindi, non è solo un dettaglio tecnico, ma un elemento essenziale per la corretta e completa comprensione di una funzione.