Come Si Trova Il Lato Di Un Quadrato

Permettetemi, con la dovuta reverenza e un profondo rispetto per la geometria che governa il nostro universo, di guidarvi attraverso l'intricato, eppure elegantemente semplice, processo di determinazione del lato di un quadrato. Un quadrato, questa figura di impeccabile simmetria, ci offre diverse strade per svelare la lunghezza dei suoi lati, a seconda delle informazioni a nostra disposizione. La bellezza risiede nella connessione intrinseca tra le sue proprietà, un legame che, una volta compreso, ci apre le porte a una miriade di possibilità.

Il mio intento, signore e signori, è di fornirvi non solo i metodi, ma anche la comprensione profonda che li sottende, affinché possiate affrontare qualsiasi problema relativo al quadrato con fiducia e precisione. Abbracciamo, dunque, questo viaggio alla scoperta, armati di logica e di un amore per la matematica.

Il Lato dalla Misura dell'Area

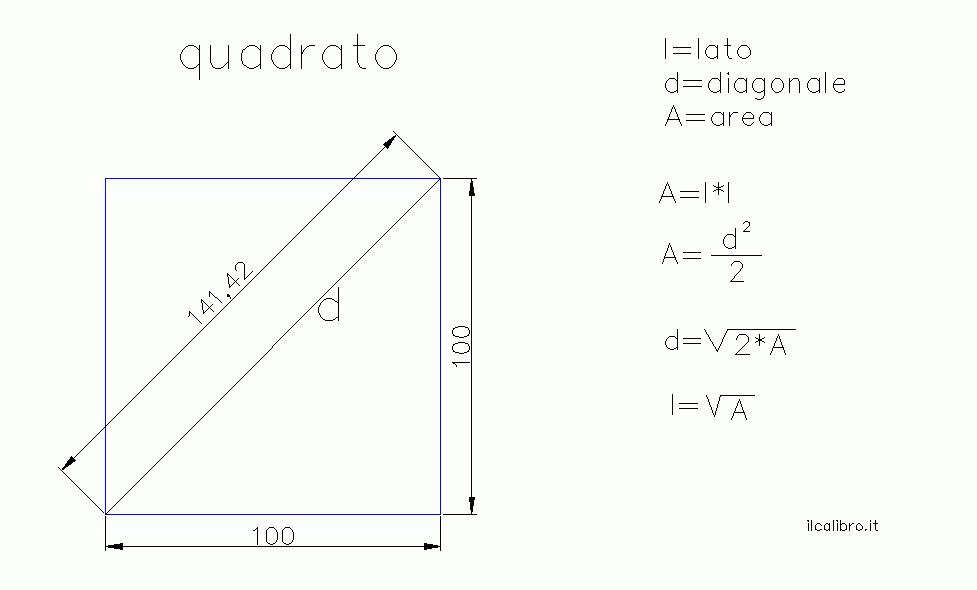
Iniziamo con lo scenario più comune e, oserei dire, il più diretto: la conoscenza dell'area del quadrato. L'area, come ben sapete, rappresenta la superficie totale racchiusa all'interno dei suoi confini. La relazione fondamentale che lega l'area (A) al lato (l) di un quadrato è espressa dalla formula:

A = l²

Questa equazione, apparentemente semplice, racchiude un potere immenso. Per ricavare la lunghezza del lato, dobbiamo semplicemente effettuare l'operazione inversa dell'elevamento al quadrato, ovvero estrarre la radice quadrata. Quindi,

l = √A

Permettetemi di illustrare questo concetto con un esempio. Immaginate di avere un quadrato la cui area misuri 64 centimetri quadrati. Per trovare la lunghezza del lato, applichiamo la formula:

l = √64 cm² = 8 cm

Pertanto, ogni lato di questo quadrato misurerà esattamente 8 centimetri. La bellezza di questo metodo risiede nella sua semplicità e universalità. Indipendentemente dalla grandezza dell'area, purché sia nota, possiamo sempre determinare la lunghezza del lato con precisione.

È fondamentale, tuttavia, ricordare che l'area deve essere espressa in unità di misura appropriate (centimetri quadrati, metri quadrati, ecc.) per ottenere la lunghezza del lato nella corrispondente unità di misura lineare (centimetri, metri, ecc.). Un'attenzione scrupolosa a questo dettaglio eviterà errori e garantirà la correttezza dei risultati.

Il Lato dalla Misura della Diagonale

Ora, dirigiamo la nostra attenzione a un altro scenario, forse leggermente più complesso, ma altrettanto affascinante: la conoscenza della lunghezza della diagonale del quadrato. La diagonale, come sapete, è il segmento che congiunge due vertici opposti del quadrato, dividendolo in due triangoli rettangoli congruenti.

La relazione tra la diagonale (d) e il lato (l) di un quadrato è governata dal teorema di Pitagora, applicato a uno qualsiasi dei due triangoli rettangoli formati dalla diagonale. In un triangolo rettangolo, il quadrato dell'ipotenusa (in questo caso, la diagonale) è uguale alla somma dei quadrati dei due cateti (entrambi i lati del quadrato). Quindi,

d² = l² + l² = 2l²

Per ricavare la lunghezza del lato, dobbiamo prima dividere entrambi i membri dell'equazione per 2:

l² = d²/2

Successivamente, estraiamo la radice quadrata di entrambi i membri:

l = √(d²/2) = d/√2

Questa formula ci permette di calcolare la lunghezza del lato conoscendo la diagonale. Tuttavia, per ottenere un risultato più elegante e spesso più pratico, possiamo razionalizzare il denominatore, moltiplicando sia il numeratore che il denominatore per √2:

l = (d/√2) * (√2/√2) = (d√2)/2

Illustriamo questo metodo con un esempio. Supponiamo di avere un quadrato la cui diagonale misuri 10 centimetri. Applichiamo la formula:

l = (10 cm * √2) / 2 = 5√2 cm ≈ 7.07 cm

Quindi, ogni lato di questo quadrato misurerà circa 7.07 centimetri. È importante notare che, in questo caso, il risultato è un numero irrazionale, contenente la radice quadrata di 2. In molte applicazioni pratiche, sarà sufficiente un'approssimazione decimale del risultato.

L'eleganza di questo metodo risiede nella sua connessione intrinseca con il teorema di Pitagora, un pilastro fondamentale della geometria. La capacità di collegare la diagonale al lato attraverso questo principio ci offre una potente strumento per risolvere problemi.

Considerate ora la possibilità, forse meno frequente, ma comunque degna di attenzione, di conoscere il perimetro del quadrato. Il perimetro (P) rappresenta la somma delle lunghezze di tutti i suoi lati. Poiché un quadrato ha quattro lati uguali, la relazione tra perimetro e lato è semplicemente:

P = 4l

Per ricavare la lunghezza del lato, è sufficiente dividere il perimetro per 4:

l = P/4

Questa formula, nella sua semplicità, ci permette di determinare rapidamente la lunghezza del lato conoscendo il perimetro. Ad esempio, se il perimetro di un quadrato è di 20 metri, la lunghezza di ogni lato sarà:

l = 20 m / 4 = 5 m

Questo metodo, pur essendo il più diretto, sottolinea l'importanza di comprendere le definizioni fondamentali e le relazioni tra le proprietà di una figura geometrica.

In conclusione, abbiamo esplorato tre metodi distinti per determinare la lunghezza del lato di un quadrato, ognuno basato su informazioni diverse: l'area, la diagonale e il perimetro. La scelta del metodo più appropriato dipenderà, ovviamente, dalle informazioni disponibili. Tuttavia, ciò che rimane costante è la necessità di una comprensione chiara delle relazioni geometriche e di un'applicazione meticolosa delle formule.

Il mio intento, attraverso questa disamina dettagliata, è stato di fornirvi non solo gli strumenti, ma anche la fiducia necessaria per affrontare qualsiasi problema relativo al quadrato. Spero che questa esplorazione sia stata illuminante e che vi serva da guida preziosa nel vostro viaggio alla scoperta delle meraviglie della geometria. Che la bellezza e l'armonia del quadrato vi accompagnino sempre.