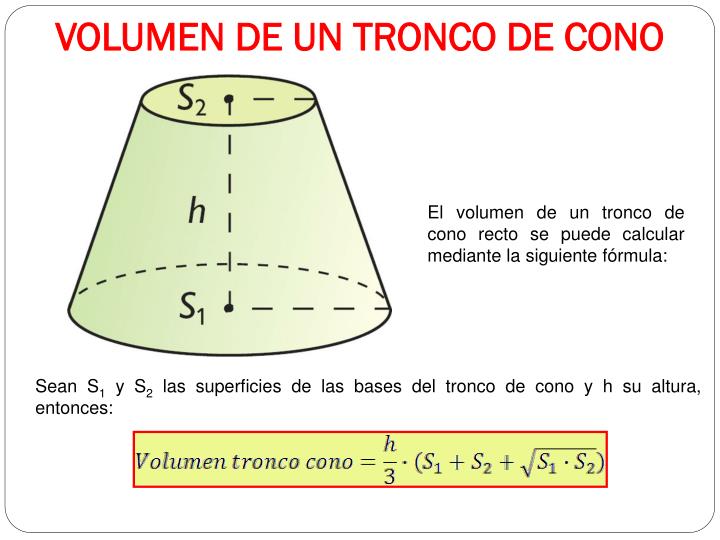
Volume Di Un Tronco Di Cono

Ti sei mai trovato di fronte a un oggetto con una forma che ti sembrava familiare ma, allo stesso tempo, leggermente diversa da quelle che conosci bene? Magari un secchio, un vaso per fiori o persino una lampada? Molto probabilmente, stavi osservando un tronco di cono. E se ti dicessi che calcolare il volume di questa figura geometrica, apparentemente complessa, è in realtà più semplice di quanto pensi?

Molte persone si sentono intimidite dalla geometria, specialmente quando si tratta di calcolare volumi. La paura di sbagliare la formula o di non capire i passaggi può bloccarci. Ma non temere! Questa guida è qui per semplificare il processo e fornirti tutti gli strumenti necessari per calcolare il volume di un tronco di cono con fiducia e precisione.

Che cos'è un Tronco di Cono?

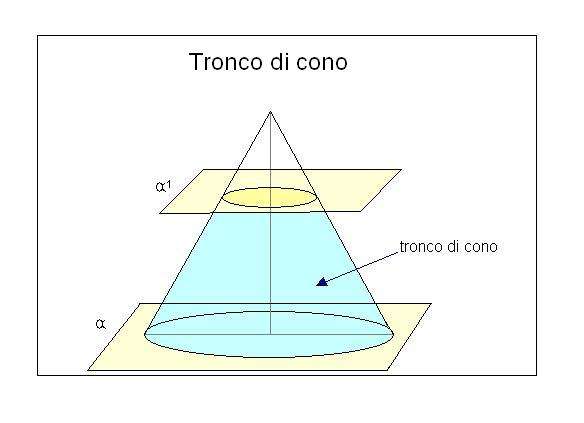
Prima di immergerci nei calcoli, cerchiamo di capire bene cosa intendiamo per tronco di cono. Immagina un cono perfetto. Ora, taglialo orizzontalmente, parallelamente alla base. La parte che rimane, quella tra la base originale e il taglio, è proprio il nostro tronco di cono! In termini più formali, è una figura geometrica solida ottenuta troncando un cono retto con un piano parallelo alla base.

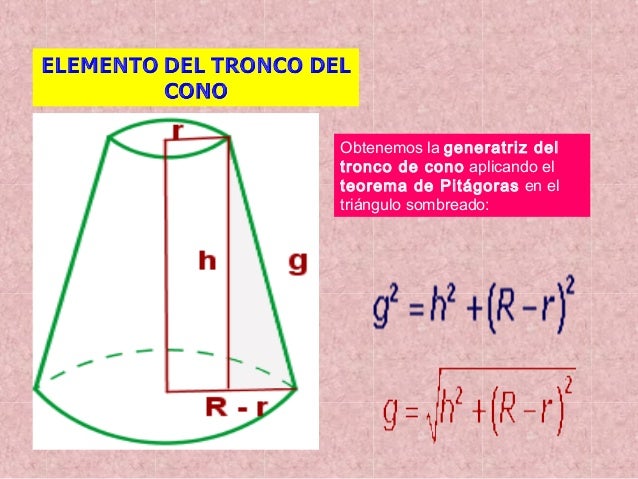
Un tronco di cono è definito da tre parametri fondamentali:

R: il raggio della base maggiore (la base originale del cono).
r: il raggio della base minore (la base ottenuta dal taglio).
h: l'altezza del tronco di cono (la distanza tra le due basi).

La Formula Magica: Calcolare il Volume

Ora veniamo al punto cruciale: la formula per calcolare il volume di un tronco di cono. È importante memorizzare o avere a portata di mano questa formula per risolvere rapidamente qualsiasi problema che coinvolga questa figura geometrica.

La formula è la seguente:

V = (1/3) * π * h * (R² + r² + R * r)

Dove:

V è il volume del tronco di cono.
π (pi greco) è una costante matematica approssimativamente uguale a 3.14159.
h è l'altezza del tronco di cono.
R è il raggio della base maggiore.
r è il raggio della base minore.

Analizziamo la Formula Passo Passo

La formula può sembrare complessa a prima vista, ma scomponiamola per comprenderla meglio:

R²: Eleva al quadrato il raggio della base maggiore.
r²: Eleva al quadrato il raggio della base minore.
R * r: Moltiplica il raggio della base maggiore per il raggio della base minore.
R² + r² + R * r: Somma i risultati ottenuti nei passaggi precedenti.
π * h * (R² + r² + R * r): Moltiplica la somma ottenuta per pi greco e per l'altezza del tronco di cono.
(1/3) * π * h * (R² + r² + R * r): Infine, moltiplica il risultato per 1/3.

Esempio Pratico: Mettiamo alla Prova la Formula

Per rendere tutto più chiaro, applichiamo la formula a un esempio concreto. Immagina di avere un secchio a forma di tronco di cono con le seguenti dimensioni:

R (raggio della base maggiore) = 15 cm
r (raggio della base minore) = 10 cm
h (altezza) = 20 cm

Applichiamo la formula:

V = (1/3) * π * 20 * (15² + 10² + 15 * 10)

V = (1/3) * π * 20 * (225 + 100 + 150)

V = (1/3) * π * 20 * 475

V ≈ 9948.37 cm³

Quindi, il volume del secchio è approssimativamente 9948.37 centimetri cubi.

Un Altro Esempio con Dati Diversi

Supponiamo di avere un vaso per fiori con le seguenti caratteristiche:

R (raggio base maggiore) = 8 cm
r (raggio base minore) = 5 cm
h (altezza) = 12 cm

Applicando la formula:

V = (1/3) * π * 12 * (8² + 5² + 8 * 5)

V = (1/3) * π * 12 * (64 + 25 + 40)

V = (1/3) * π * 12 * 129

V ≈ 1619.76 cm³

Il volume del vaso è quindi circa 1619.76 centimetri cubi.

Consigli Utili per Evitare Errori

Anche se la formula è semplice, è facile commettere errori di calcolo. Ecco alcuni consigli per evitarli:

Verifica le unità di misura: Assicurati che tutte le misure (raggio e altezza) siano espresse nella stessa unità (es. centimetri, metri). Se necessario, converti le misure prima di applicare la formula.
Usa una calcolatrice: Per evitare errori di calcolo manuale, usa una calcolatrice scientifica, soprattutto se i numeri sono grandi o decimali.
Ricontrolla i passaggi: Dopo aver calcolato il volume, ricontrolla tutti i passaggi per assicurarti di non aver commesso errori di digitazione o di calcolo.
Arrotonda correttamente: Se necessario, arrotonda il risultato finale alla cifra decimale appropriata.

Applicazioni Pratiche del Calcolo del Volume del Tronco di Cono

Il calcolo del volume del tronco di cono ha diverse applicazioni pratiche nella vita di tutti i giorni e in vari settori professionali:

Ingegneria: Nel calcolo della capacità di serbatoi, silos e altre strutture con forma conica troncata.
Architettura: Nella progettazione di tetti conici, colonne e altri elementi architettonici.
Industria alimentare: Nel calcolo del volume di contenitori per alimenti, come bicchieri, vaschette e imballaggi.
Giardinaggio: Nel calcolo del volume di vasi per piante e fioriere.
Fai da te: Nel calcolo del materiale necessario per costruire oggetti conici, come paralumi o elementi decorativi.

Strumenti Online per Calcolare il Volume

Se non ti senti sicuro nel calcolare il volume manualmente, puoi utilizzare diversi calcolatori online gratuiti. Basta inserire i valori di R, r e h, e il calcolatore farà il resto! Alcuni di questi calcolatori offrono anche la possibilità di visualizzare i passaggi del calcolo, il che può essere utile per capire meglio il processo.

Tuttavia, è importante capire la formula e il processo di calcolo anche se si utilizzano strumenti online. Questo ti permetterà di verificare l'accuratezza dei risultati e di risolvere problemi anche quando non hai accesso a un calcolatore.

Conclusione: Non Aver Paura della Geometria!

Calcolare il volume di un tronco di cono può sembrare complicato all'inizio, ma con la formula giusta e un po' di pratica, diventa un'operazione semplice e alla portata di tutti. Ricorda, la chiave è capire la formula, seguire i passaggi con attenzione e non aver paura di sperimentare.

Spero che questa guida ti sia stata utile. Ora sei pronto per affrontare qualsiasi problema che coinvolga il calcolo del volume di un tronco di cono. Buona fortuna!