Verifica Teorema Di Pitagora Con Soluzioni

Il Teorema di Pitagora è uno dei pilastri fondamentali della geometria euclidea e della matematica in generale. La sua importanza trascende la pura teoria, trovando applicazioni innumerevoli in campi come l'ingegneria, l'architettura, la fisica e la navigazione. Questo articolo esplorerà in dettaglio il teorema, le sue implicazioni e diversi metodi per verificarlo, con esempi pratici.

Cos'è il Teorema di Pitagora?

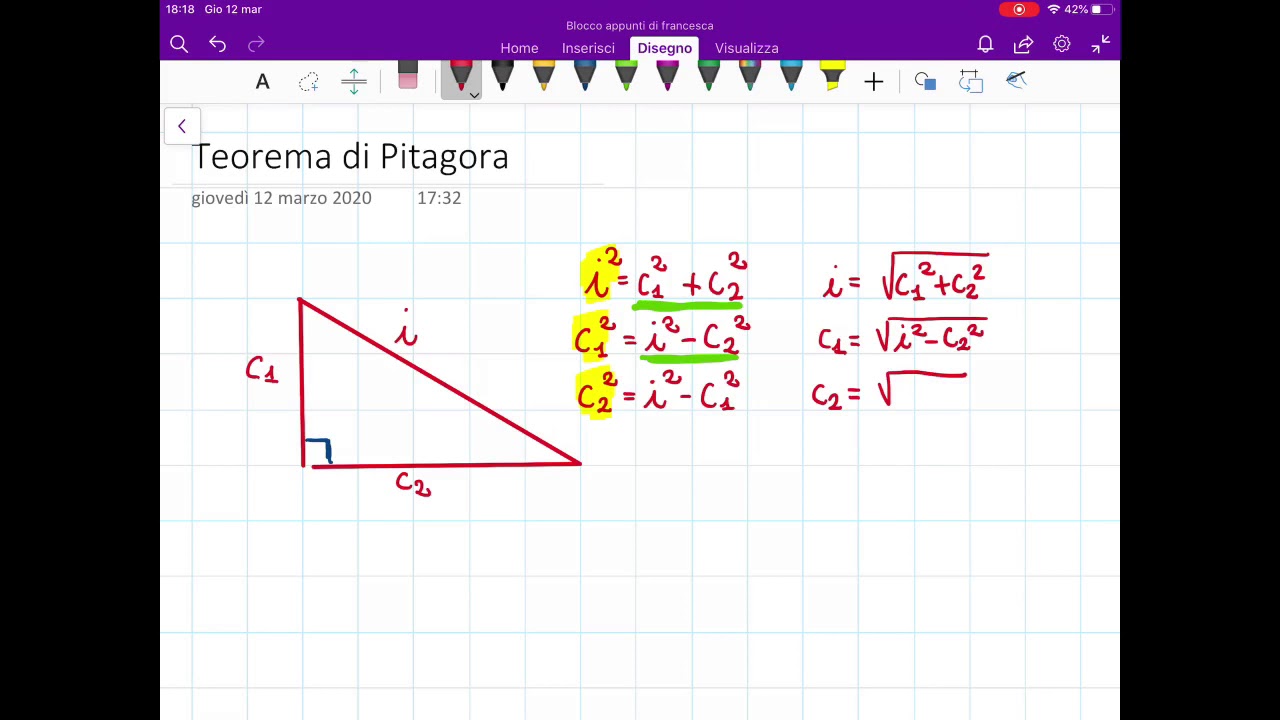
Il Teorema di Pitagora stabilisce una relazione fondamentale tra i lati di un triangolo rettangolo. Un triangolo rettangolo è un triangolo che ha un angolo di 90 gradi (un angolo retto). I lati che formano l'angolo retto sono chiamati cateti, mentre il lato opposto all'angolo retto è chiamato ipotenusa. Il teorema afferma che:

"In ogni triangolo rettangolo, l'area del quadrato costruito sull'ipotenusa è uguale alla somma delle aree dei quadrati costruiti sui cateti."

Matematicamente, questo si esprime come:

a² + b² = c²

Dove:

• a e b sono le lunghezze dei cateti.
• c è la lunghezza dell'ipotenusa.

Importanza del Teorema

La sua importanza deriva dalla sua universalità. Vale per ogni triangolo rettangolo, indipendentemente dalle dimensioni dei lati. Questa universalità lo rende uno strumento potente per risolvere problemi geometrici e non solo. Ad esempio, permette di calcolare la lunghezza di un lato di un triangolo rettangolo conoscendo gli altri due, oppure di determinare se un triangolo è rettangolo conoscendo le lunghezze dei suoi lati.

Verifica del Teorema di Pitagora: Metodi Diversi

Esistono diverse dimostrazioni e verifiche del Teorema di Pitagora, che spaziano da approcci geometrici a dimostrazioni algebriche. Esploreremo alcuni dei metodi più comuni e intuitivi.

Dimostrazione Geometrica Visiva

Una delle dimostrazioni più semplici e intuitive è di tipo geometrico. Consideriamo un quadrato di lato (a + b). All'interno di questo quadrato, possiamo disporre quattro triangoli rettangoli identici con cateti di lunghezza a e b, e ipotenusa di lunghezza c. Questi triangoli sono disposti in modo tale da formare un quadrato più piccolo al centro.

L'area del quadrato grande è (a + b)² = a² + 2ab + b². L'area dei quattro triangoli rettangoli è 4 * (1/2 * a * b) = 2ab. L'area del quadrato centrale è c².

Pertanto, l'area del quadrato grande può essere espressa anche come la somma dell'area dei quattro triangoli e dell'area del quadrato centrale: a² + 2ab + b² = 2ab + c².

Semplificando l'equazione, otteniamo: a² + b² = c², confermando il teorema.

Verifica con Triplette Pitagoriche

Le Triplette Pitagoriche sono insiemi di tre numeri interi positivi a, b e c, che soddisfano l'equazione a² + b² = c². Esempi comuni includono (3, 4, 5), (5, 12, 13), (8, 15, 17) e (7, 24, 25). Utilizzando queste triplette, possiamo costruire triangoli rettangoli e verificare che le lunghezze dei lati rispettino la relazione pitagorica.

Ad esempio, se prendiamo la tripletta (3, 4, 5), costruiamo un triangolo rettangolo con cateti di lunghezza 3 e 4. L'ipotenusa avrà lunghezza 5. Verifichiamo che 3² + 4² = 9 + 16 = 25 = 5². Questo conferma il teorema.

Possiamo ripetere questo processo con altre triplette pitagoriche per ulteriori verifiche. L'uso di numeri interi rende la verifica più semplice e concreta.

Dimostrazione Algebrica

Esistono anche dimostrazioni puramente algebriche. Consideriamo un triangolo rettangolo con cateti a e b, e ipotenusa c. Possiamo calcolare l'area del triangolo in due modi diversi. Primo, come 1/2 * a * b. Secondo, possiamo usare la formula di Erone per calcolare l'area in termini dei lati. Tuttavia, una dimostrazione algebrica più diretta coinvolge la similitudine dei triangoli.

Consideriamo l'altezza relativa all'ipotenusa. Questa altezza divide il triangolo rettangolo in due triangoli più piccoli, entrambi simili al triangolo originale e simili tra loro. Utilizzando le proprietà dei triangoli simili, possiamo stabilire proporzioni tra i lati e, attraverso manipolazioni algebriche, arrivare alla relazione a² + b² = c².

Utilizzo di Software di Geometria Dinamica

Strumenti come GeoGebra offrono un modo interattivo per verificare il teorema. Possiamo costruire un triangolo rettangolo, misurare le lunghezze dei suoi lati e calcolare a² + b² e c². Il software mostrerà che i due valori sono uguali, confermando visivamente e numericamente il teorema. La bellezza di questi strumenti è la possibilità di modificare il triangolo e osservare che la relazione pitagorica rimane valida.

Esempi Reali e Applicazioni Pratiche

Il Teorema di Pitagora ha un'ampia gamma di applicazioni pratiche.

Architettura e Ingegneria

Gli architetti e gli ingegneri utilizzano il Teorema di Pitagora per calcolare le lunghezze diagonali in edifici e strutture. Ad esempio, per assicurarsi che un angolo di una stanza sia veramente retto, possono misurare le lunghezze dei due lati adiacenti e la diagonale. Se le lunghezze soddisfano il teorema, l'angolo è di 90 gradi.

Inoltre, viene utilizzato nella progettazione di ponti, tetti e altre strutture che richiedono calcoli precisi delle distanze e degli angoli.

Navigazione

I navigatori utilizzano il Teorema di Pitagora per calcolare le distanze tra punti su una mappa. Se un punto si trova a est e a nord di un altro punto, la distanza tra i due può essere calcolata utilizzando il teorema, considerando le distanze a est e a nord come i cateti di un triangolo rettangolo.

Costruzioni

Nelle costruzioni, il teorema è utile per livellare terreni, costruire fondamenta e garantire che le strutture siano perpendicolari. I carpentieri lo usano per assicurarsi che gli angoli siano retti quando costruiscono telai per porte e finestre.

Fisica

In fisica, il Teorema di Pitagora è utilizzato per calcolare la magnitudo di vettori. Ad esempio, se un oggetto si muove con una velocità orizzontale e una velocità verticale, la velocità risultante può essere calcolata utilizzando il teorema.

Esempio Concreto: Calcolo della diagonale di uno schermo

Consideriamo uno schermo televisivo con una larghezza di 50 pollici e un'altezza di 30 pollici. Per calcolare la lunghezza della diagonale dello schermo, possiamo utilizzare il Teorema di Pitagora:

diagonale² = larghezza² + altezza²

diagonale² = 50² + 30² = 2500 + 900 = 3400

diagonale = √3400 ≈ 58.31 pollici

Quindi, la diagonale dello schermo è di circa 58.31 pollici.

Limitazioni e Considerazioni

È fondamentale ricordare che il Teorema di Pitagora si applica solo ai triangoli rettangoli. Non può essere utilizzato direttamente per calcolare le relazioni tra i lati di triangoli acutangoli o ottusangoli. In questi casi, è necessario utilizzare le leggi dei seni e dei coseni, che sono generalizzazioni del teorema di Pitagora.

Inoltre, è importante notare che il teorema è basato sulla geometria euclidea. In geometrie non euclidee, come la geometria sferica o iperbolica, il teorema non è valido.

Conclusione

Il Teorema di Pitagora è un concetto fondamentale con un'importanza che va ben oltre la matematica pura. La sua applicazione in diversi campi, dalla costruzione all'ingegneria alla navigazione, lo rende uno strumento essenziale per risolvere problemi pratici. Sperimentare con le diverse verifiche presentate in questo articolo, sia geometriche che algebriche, aiuta a consolidare la comprensione del teorema e ad apprezzare la sua eleganza e universalità. Ti invitiamo a utilizzare gli strumenti di geometria dinamica come GeoGebra per esplorare ulteriormente le implicazioni del Teorema di Pitagora e a cercare le sue applicazioni nel mondo che ti circonda.