Una Molla Di Massa Trascurabile E Costante Elastica 3

Capita a tutti, almeno una volta nella vita, di imbattersi in concetti apparentemente astratti della fisica che sembrano relegati al mondo dei libri di testo. Ma la verità è che la fisica, e concetti come quello di una molla ideale, ci circondano e influenzano la nostra vita quotidiana più di quanto immaginiamo. Parliamo oggi di un elemento fondamentale: una molla di massa trascurabile e costante elastica pari a 3. Cosa significa esattamente, e perché dovremmo interessarcene?

Proviamo a immedesimarci. Avete presente la sospensione di un'auto che rende più confortevole il viaggio anche su strade dissestate? O il meccanismo di un orologio che segna il tempo con precisione? Dietro a questi sistemi, spesso complessi, si celano principi fisici basilari, tra cui quello dell'elasticità e, idealmente, delle molle. Ecco perché comprendere il concetto di molla ideale è cruciale.

La Molla Ideale: Un Modello Utile

Partiamo dal presupposto che una molla perfetta, o ideale, è un'astrazione. Nella realtà, ogni molla ha una massa, un attrito interno e altre imperfezioni. Tuttavia, per semplificare i calcoli e comprendere i principi fondamentali, spesso si ricorre al modello della molla ideale, definita da due caratteristiche principali:

• Massa Trascurabile: Si assume che la massa della molla sia così piccola da poter essere ignorata nei calcoli. Questo semplifica notevolmente l'analisi del sistema in cui la molla è inserita.
• Costante Elastica (k): Questo valore, nel nostro caso pari a 3, quantifica la rigidità della molla. Esprime la forza necessaria per allungare o comprimere la molla di una certa lunghezza. Un valore di k=3 significa che servono 3 Newton di forza per deformare la molla di 1 metro (o le unità di misura corrispondenti).

La costante elastica, spesso indicata con la lettera 'k', è misurata in Newton per metro (N/m) o in unità equivalenti. Nel nostro esempio, con k=3, abbiamo una molla relativamente morbida. Una molla con k=100 sarebbe molto più rigida e richiederebbe una forza maggiore per essere deformata.

La Legge di Hooke

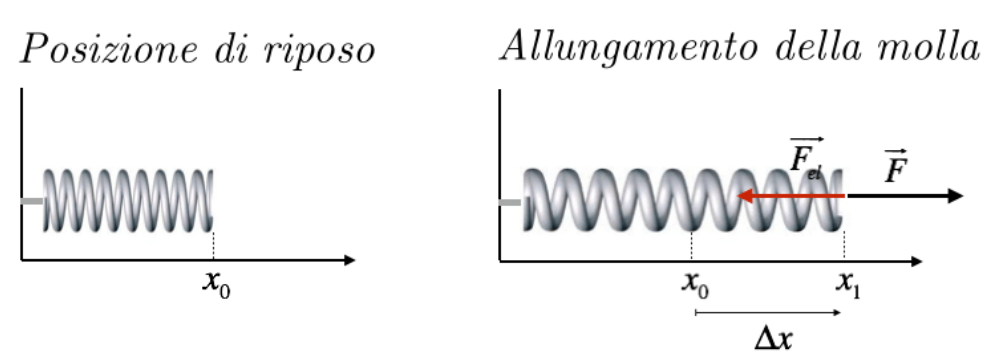
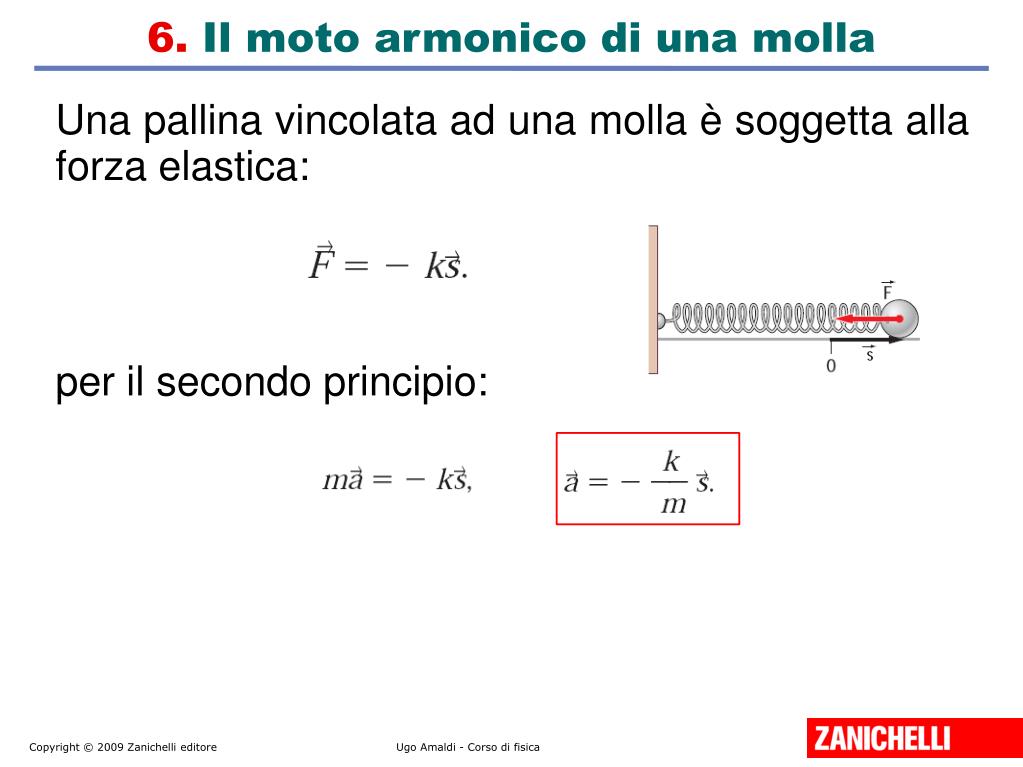
Il comportamento di una molla ideale è descritto dalla Legge di Hooke, una delle leggi fondamentali della fisica. Questa legge afferma che la forza esercitata da una molla è direttamente proporzionale alla sua deformazione (allungamento o compressione) rispetto alla sua posizione di riposo. Matematicamente, si esprime come:

F = -k * x

Dove:

• F è la forza esercitata dalla molla.
• k è la costante elastica della molla.
• x è la deformazione della molla (allungamento o compressione).

Il segno meno indica che la forza esercitata dalla molla è opposta alla direzione della deformazione. Se allunghiamo la molla, la molla esercita una forza che tende a riportarla alla sua posizione di riposo. Se la comprimiamo, la molla esercita una forza che tende a farla espandere.

Impatto nel Mondo Reale

Anche se può sembrare teorico, il concetto di molla ideale e la Legge di Hooke hanno un impatto enorme in diverse aree:

• Ingegneria Meccanica: Le molle sono utilizzate in una vasta gamma di applicazioni, dalle sospensioni delle auto ai sistemi di ammortizzazione, fino ai meccanismi di chiusura delle porte e ai sistemi di fissaggio. La comprensione della costante elastica è cruciale per progettare sistemi efficienti e sicuri.
• Medicina: Le molle sono utilizzate in dispositivi medici come siringhe, pinze e persino in alcuni tipi di protesi. La precisione e l'affidabilità di questi dispositivi dipendono dalla corretta progettazione delle molle.
• Strumentazione: Gli strumenti di misura, come le bilance e i dinamometri, spesso utilizzano molle per convertire una forza in una misurazione. La calibrazione di questi strumenti si basa sulla conoscenza precisa della costante elastica delle molle utilizzate.
• Sport: Attrezzature sportive, come trampolini, molle per suspension training e attrezzi da palestra utilizzano la proprietà elastica delle molle.

Prendiamo l'esempio della sospensione di un'automobile. Il sistema di sospensione include molle (generalmente elicoidali) e ammortizzatori. Le molle assorbono l'energia proveniente dalle irregolarità della strada, mentre gli ammortizzatori smorzano le oscillazioni, impedendo all'auto di rimbalzare eccessivamente. La costante elastica delle molle è un parametro fondamentale per determinare il comfort di guida e la stabilità del veicolo.

Considerazioni e Controindicazioni

È importante riconoscere i limiti del modello ideale. Come accennato, le molle reali hanno massa, attrito e possono subire deformazioni permanenti se sottoposte a forze eccessive. Inoltre, la Legge di Hooke vale solo entro un certo limite di deformazione. Se la molla viene allungata o compressa troppo, può perdere la sua elasticità e non ritornare alla sua forma originale. Questo è noto come limite elastico. Andare oltre questo limite può portare alla rottura della molla.

Alcuni potrebbero sostenere che concentrarsi su modelli ideali è inutile, dato che la realtà è sempre più complessa. Tuttavia, i modelli ideali sono strumenti potenti per imparare i concetti di base e costruire la nostra comprensione del mondo fisico. Servono come punto di partenza, un'approssimazione che possiamo poi raffinare includendo ulteriori dettagli e complessità.

Risolvere i Problemi con una Molla di k=3

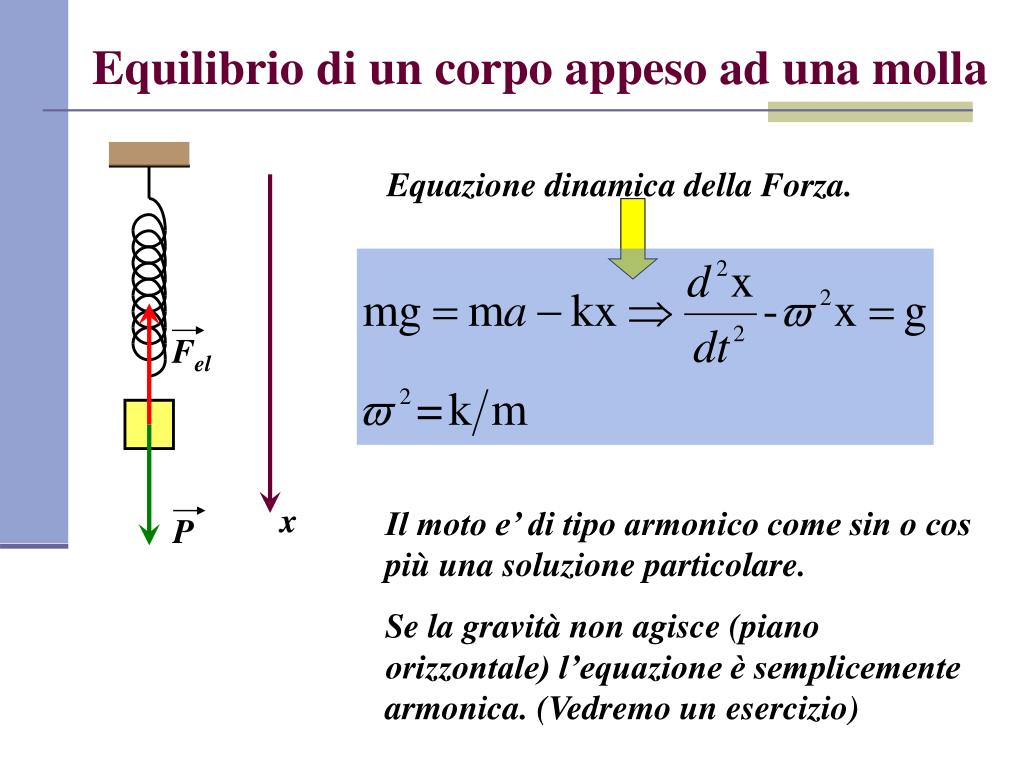
Vediamo un esempio pratico. Immaginiamo di avere una molla con costante elastica k=3 N/m. Se appendiamo un peso di 6 Newton alla molla, di quanto si allungherà?

Utilizziamo la Legge di Hooke: F = -k * x. In questo caso, F = 6 N e k = 3 N/m. Risolvendo per x, otteniamo:

x = -F / k = -6 N / 3 N/m = -2 metri

Il segno meno indica che la molla si allunga (la deformazione è nella direzione opposta alla forza). Quindi, la molla si allungherà di 2 metri.

Soluzioni e Approcci Pratici

Come possiamo sfruttare la conoscenza della molla ideale con k=3 per risolvere problemi pratici?

• Progettazione di Sistemi di Ammortizzazione: Se stiamo progettando un sistema di ammortizzazione, possiamo utilizzare la costante elastica per calcolare la forza necessaria per comprimere la molla di una determinata quantità. Questo ci aiuta a scegliere la molla giusta per l'applicazione specifica.
• Calibrazione di Strumenti di Misura: Possiamo utilizzare una molla con una costante elastica nota per calibrare strumenti di misura, come le bilance a molla. Applicando pesi noti alla molla e misurando la sua deformazione, possiamo determinare la precisione dello strumento.
• Analisi di Sistemi Meccanici: La conoscenza della Legge di Hooke e della costante elastica ci permette di analizzare sistemi meccanici complessi, come quelli presenti nelle macchine e nei dispositivi elettronici. Possiamo utilizzare questi concetti per prevedere il comportamento del sistema e ottimizzarne le prestazioni.

Un approccio utile è quello di utilizzare software di simulazione. Questi software consentono di modellare sistemi complessi che includono molle e altri componenti meccanici, simulandone il comportamento sotto diverse condizioni di carico. Questo è particolarmente utile per la progettazione di sistemi avanzati.

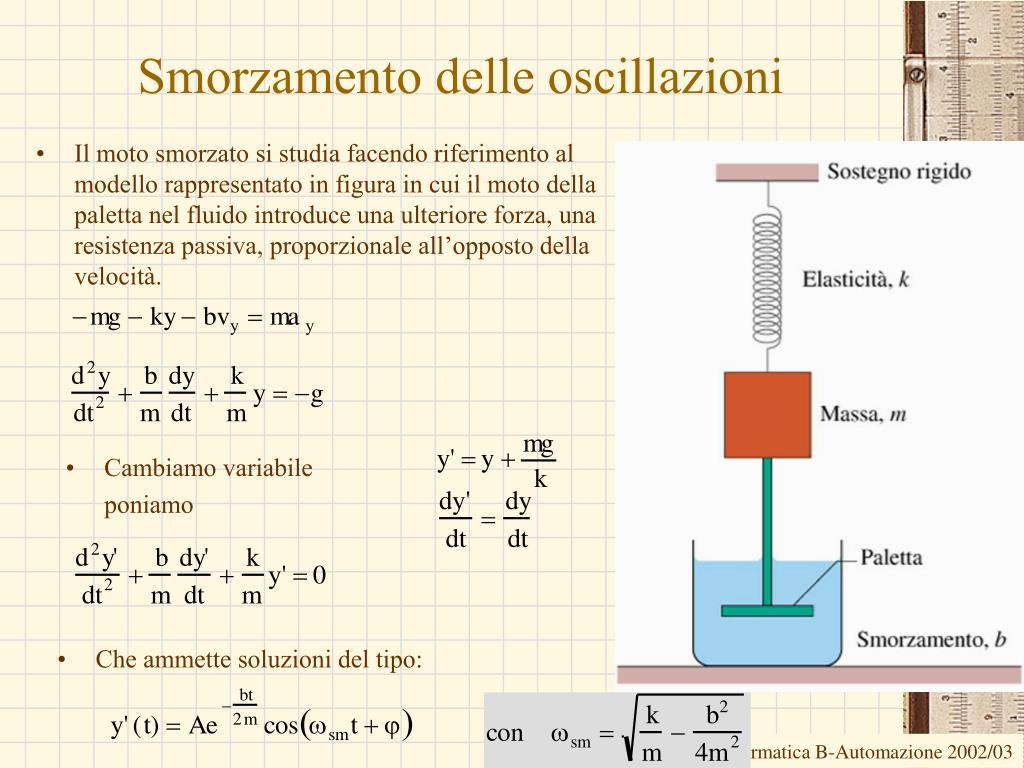
Un altro aspetto da considerare è la risonanza. Ogni sistema che include una molla ha una frequenza naturale di oscillazione. Se il sistema viene eccitato a questa frequenza, può verificarsi un fenomeno di risonanza, con conseguenti oscillazioni di ampiezza crescente che possono danneggiare il sistema. È quindi importante progettare il sistema in modo da evitare la risonanza.

Infine, è fondamentale considerare i materiali. La scelta del materiale per la molla influisce sulla sua costante elastica, sulla sua resistenza alla fatica e sulla sua durata nel tempo. Materiali come l'acciaio armonico sono spesso utilizzati per la fabbricazione di molle grazie alle loro eccellenti proprietà elastiche.

Speriamo che questo articolo abbia chiarito il concetto di molla ideale e la sua rilevanza nel mondo reale. Ora, vi invitiamo a riflettere: In quali altri oggetti o sistemi intorno a voi riconoscete l'azione di una molla, e come pensate che la sua costante elastica influenzi il loro funzionamento?