Triangolo Rettangolo Circoscritto In Una Circonferenza

Capita spesso di trovarci di fronte a concetti geometrici che, a prima vista, sembrano astratti e lontani dalla nostra quotidianità. Ma la geometria, come vedremo, è sorprendentemente presente nelle cose che ci circondano. Immagina di dover progettare un edificio, un ponte, o anche semplicemente di appendere un quadro al muro: le leggi geometriche sono lì, a guidarci, spesso in modo inconscio. Oggi, ci concentreremo su un particolare tipo di figura: il triangolo rettangolo circoscritto in una circonferenza. Questo argomento potrebbe sembrare complesso, ma cercheremo di renderlo accessibile a tutti, svelandone le proprietà e le applicazioni pratiche.

Molti di noi ricordano le lezioni di geometria a scuola, magari con un certo fastidio. Formule, teoremi, dimostrazioni... tutto può sembrare ostico e poco stimolante. Tuttavia, la bellezza della geometria risiede nella sua capacità di descrivere il mondo che ci circonda in modo preciso ed elegante. Capire il triangolo rettangolo circoscritto non è solo un esercizio teorico, ma può aiutarci a sviluppare un pensiero logico e a risolvere problemi concreti.

Cos'è un Triangolo Rettangolo Circoscritto?

Partiamo dalle definizioni fondamentali, per assicurarci che tutti siano sullo stesso piano:

• Triangolo Rettangolo: Un triangolo con un angolo di 90 gradi (angolo retto). I lati che formano l'angolo retto sono chiamati cateti, mentre il lato opposto all'angolo retto è l'ipotenusa.
• Circonferenza Circoscritta: Una circonferenza che passa per tutti i vertici di un poligono (in questo caso, un triangolo).
• Circoscritto: significa "descritto attorno". Quindi, un triangolo rettangolo circoscritto in una circonferenza è un triangolo rettangolo i cui tre vertici giacciono sulla circonferenza.

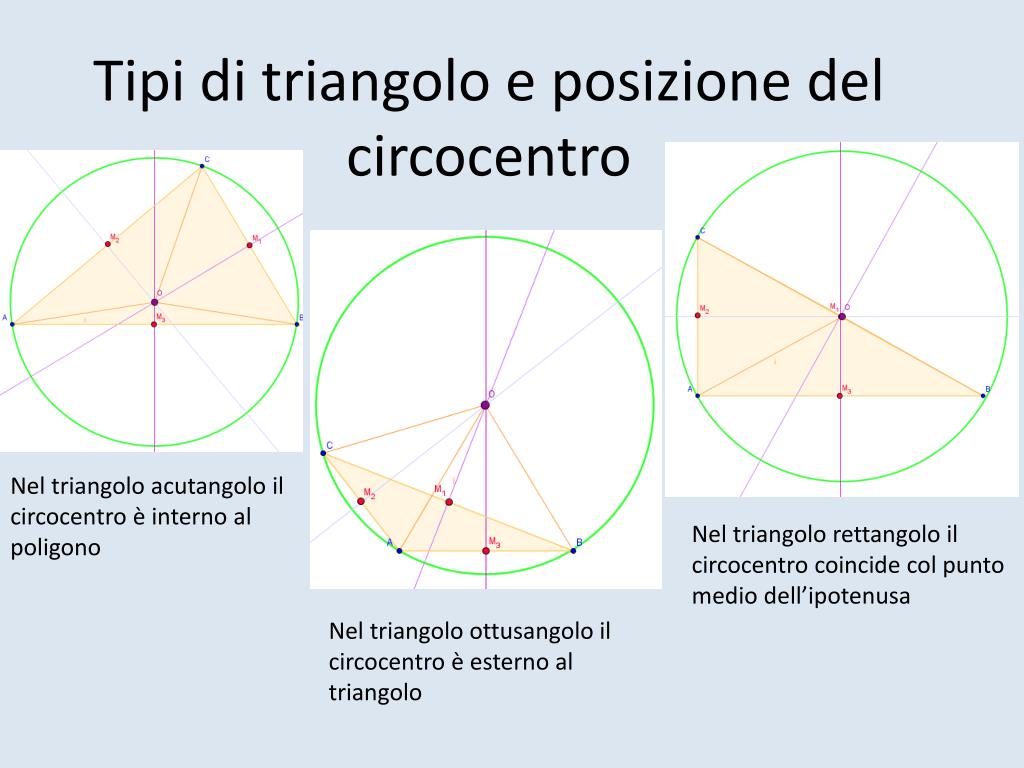
La cosa fondamentale da ricordare è che, per un triangolo rettangolo circoscritto, l'ipotenusa coincide sempre con il diametro della circonferenza. Questo è un teorema importantissimo che ci permette di collegare le proprietà del triangolo a quelle della circonferenza.

Teorema Fondamentale

Il teorema che lega il triangolo rettangolo circoscritto alla circonferenza è il seguente: "Un triangolo rettangolo è inscritto in una semicirconferenza avente per diametro l'ipotenusa". In altre parole, se prendiamo un triangolo rettangolo e disegniamo una circonferenza che passa per i suoi tre vertici, il centro di quella circonferenza si troverà esattamente a metà dell'ipotenusa.

Questo teorema ha una dimostrazione elegante che si basa sulle proprietà degli angoli al centro e degli angoli alla circonferenza. Tuttavia, per il nostro scopo, è sufficiente capire l'importanza del legame tra l'ipotenusa e il diametro.

Perché è Importante?

Potresti chiederti: "Ok, abbiamo un triangolo rettangolo e una circonferenza, ma perché dovrebbe interessarmi?". La risposta è che questa configurazione geometrica si presta a diverse applicazioni pratiche e teoriche.

• Costruzioni Geometriche: Possiamo utilizzare questa proprietà per costruire un angolo retto con riga e compasso. Tracciamo una circonferenza, disegniamo un diametro, e scegliamo un punto qualsiasi sulla circonferenza (diverso dagli estremi del diametro). Collegando quel punto agli estremi del diametro, otteniamo un triangolo rettangolo.
• Calcolo di Aree e Perimetri: Conoscendo il raggio della circonferenza (e quindi il diametro, che è l'ipotenusa) e la lunghezza di uno dei cateti, possiamo calcolare l'area e il perimetro del triangolo rettangolo utilizzando il teorema di Pitagora.
• Problemi di Geometria: Molti problemi di geometria coinvolgono triangoli rettangoli circoscritti. La conoscenza del teorema fondamentale ci permette di semplificare la risoluzione di questi problemi.

Immagina di essere un architetto e di dover progettare una finestra a forma di semicerchio con un rinforzo diagonale che forma un triangolo rettangolo. Conoscere le proprietà del triangolo rettangolo circoscritto ti permette di calcolare con precisione la lunghezza del rinforzo e l'area della finestra.

Esempio Pratico

Supponiamo di avere una circonferenza di raggio 5 cm. Disegniamo un triangolo rettangolo inscritto in questa circonferenza. Sappiamo che l'ipotenusa del triangolo è uguale al diametro della circonferenza, quindi l'ipotenusa misura 10 cm. Se uno dei cateti misura 6 cm, possiamo calcolare la lunghezza dell'altro cateto usando il teorema di Pitagora:

a² + b² = c²

Dove a e b sono i cateti e c è l'ipotenusa.

6² + b² = 10²

36 + b² = 100

b² = 64

b = 8 cm

Quindi, l'altro cateto misura 8 cm. Possiamo ora calcolare l'area del triangolo: (6 cm * 8 cm) / 2 = 24 cm².

Affrontare le Obiezioni

Alcuni potrebbero sostenere che la geometria è una disciplina troppo teorica e poco utile nella vita reale. È vero che molte formule e teoremi sembrano astratti, ma la geometria ci fornisce gli strumenti per comprendere e descrivere il mondo che ci circonda. La capacità di visualizzare e manipolare figure geometriche è fondamentale in molti campi, dall'ingegneria all'arte.

Un'altra obiezione potrebbe essere che la tecnologia moderna rende la geometria obsoleta. Con software di progettazione avanzati, non c'è più bisogno di conoscere i teoremi geometrici. Tuttavia, la tecnologia è solo uno strumento. Per utilizzarlo efficacemente, è necessario avere una solida base di conoscenze teoriche. Conoscere la geometria ci permette di interpretare i risultati dei software di progettazione e di prendere decisioni informate.

Soluzioni e Prospettive Future

Per rendere la geometria più accessibile e coinvolgente, è importante:

• Utilizzare esempi concreti: Collegare i concetti geometrici a situazioni reali aiuta a rendere l'apprendimento più significativo.
• Sperimentare con software interattivi: I software di geometria dinamica permettono di manipolare figure geometriche e di visualizzare le loro proprietà in modo intuitivo.
• Incoraggiare la risoluzione di problemi: Affrontare problemi pratici che richiedono l'applicazione dei concetti geometrici aiuta a sviluppare un pensiero critico e creativo.

In futuro, la geometria continuerà a giocare un ruolo fondamentale in molti settori. L'intelligenza artificiale, la robotica, la realtà virtuale e aumentata si basano fortemente su concetti geometrici per creare mondi virtuali e robot autonomi. Comprendere la geometria è quindi essenziale per affrontare le sfide del futuro.

Conclusione

Il triangolo rettangolo circoscritto è un esempio di come un concetto geometrico apparentemente semplice possa nascondere proprietà interessanti e applicazioni pratiche. La geometria non è solo una serie di formule da memorizzare, ma uno strumento potente per comprendere il mondo che ci circonda.

Abbiamo visto come il legame tra l'ipotenusa del triangolo e il diametro della circonferenza ci permette di risolvere problemi, costruire angoli retti e visualizzare relazioni geometriche. Abbiamo anche affrontato alcune obiezioni comuni e proposto soluzioni per rendere la geometria più accessibile.

Ora, ti invito a riflettere: come potresti applicare le conoscenze acquisite oggi nella tua vita quotidiana? Quali problemi potresti risolvere utilizzando la geometria? Prendi un foglio di carta, disegna un triangolo rettangolo circoscritto e sperimenta con le sue proprietà. La geometria è un mondo da scoprire, e le possibilità sono infinite!