Triangolo Equilatero Circoscritto In Una Circonferenza

Ti sei mai trovato di fronte a un problema di geometria che ti sembrava insormontabile, come calcolare le dimensioni di un triangolo equilatero inscritto o circoscritto a una circonferenza? Non sei solo! Molti studenti e appassionati di matematica si scontrano con questa sfida. L'obiettivo di questo articolo è di rendere questo concetto cristallino, fornendo una guida chiara e pratica.
Inizieremo esplorando le proprietà fondamentali dei triangoli equilateri e delle circonferenze, per poi addentrarci nel cuore del problema: la relazione tra un triangolo equilatero circoscritto a una circonferenza. Vedremo come calcolare il lato del triangolo in base al raggio della circonferenza e viceversa. Cercheremo di rendere tutto il più semplice possibile, con esempi pratici e formule chiare.
Concetti Fondamentali: Prepariamo il Terreno
Prima di affrontare il triangolo equilatero circoscritto, è cruciale avere ben chiari alcuni concetti di base. Partiamo dalle definizioni:
Triangolo Equilatero: L'Eleganza della Simmetria
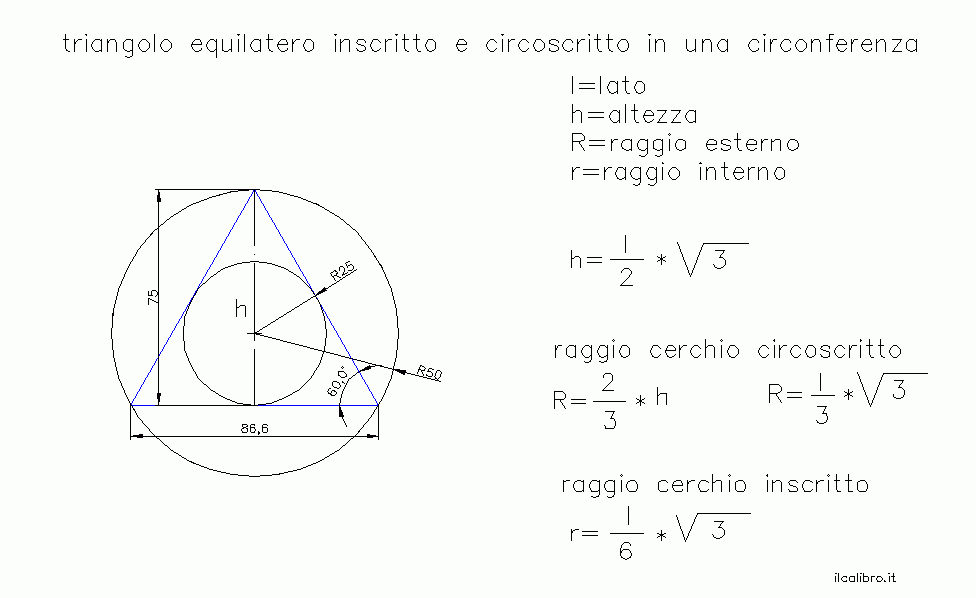
Un triangolo equilatero è un poligono con tre lati uguali e tre angoli uguali, ciascuno di 60 gradi. Questa simmetria lo rende una figura geometrica particolarmente elegante e facile da analizzare. Ogni lato è identico, e l'altezza divide il triangolo in due triangoli rettangoli congruenti, il che ci permette di applicare il teorema di Pitagora per calcolare l'altezza in funzione del lato.
Circonferenza: Un Insieme di Punti Equidistanti
Una circonferenza è l'insieme di tutti i punti equidistanti da un punto centrale chiamato centro. La distanza tra un punto qualsiasi della circonferenza e il centro è detta raggio. La circonferenza ha un ruolo fondamentale nella geometria, e la sua relazione con altre figure geometriche, come i triangoli, è oggetto di studio da secoli.
Il Triangolo Equilatero Circoscritto: Un'Analisi Approfondita
Ora arriviamo al punto cruciale: il triangolo equilatero circoscritto a una circonferenza. Cosa significa esattamente?
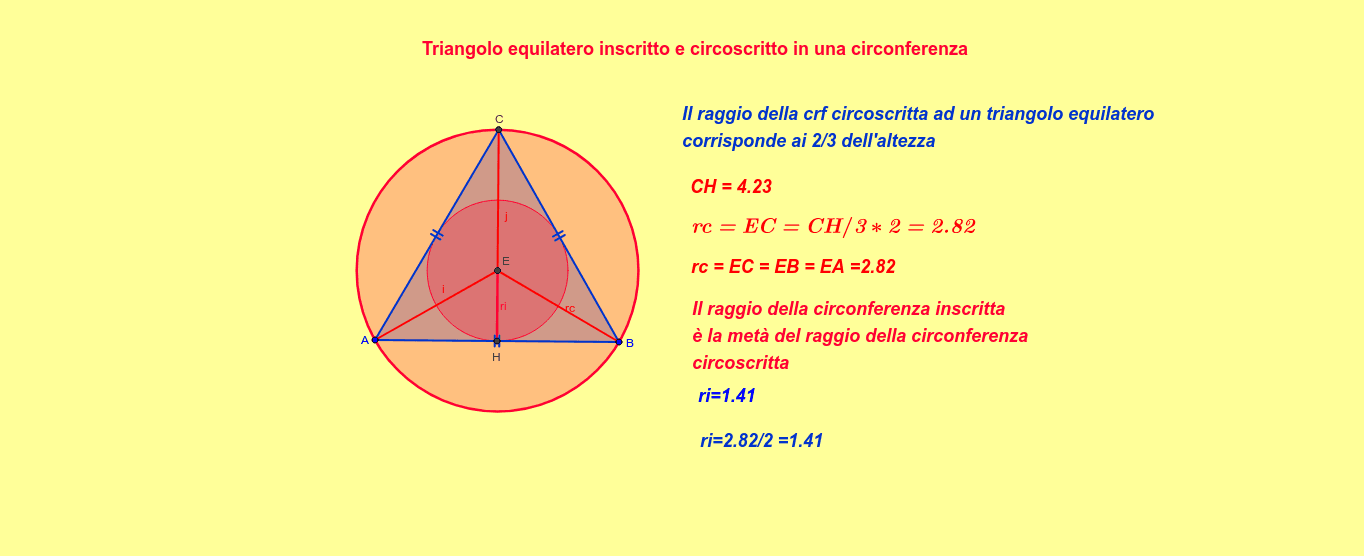
Un triangolo equilatero è detto circoscritto a una circonferenza se tutti e tre i suoi lati sono tangenti alla circonferenza. In altre parole, la circonferenza si trova all'interno del triangolo, e tocca ogni lato in un solo punto. Questo punto di tangenza è importante perché la retta che congiunge il centro della circonferenza con il punto di tangenza è perpendicolare al lato del triangolo.
La Relazione Chiave: Raggio e Lato
La relazione tra il raggio della circonferenza (r) e il lato del triangolo equilatero circoscritto (L) è fondamentale per risolvere molti problemi di geometria. Questa relazione può essere espressa attraverso la seguente formula:
L = 2√3 * r
Questa formula ci dice che il lato del triangolo è uguale a due volte la radice quadrata di tre, moltiplicato per il raggio della circonferenza. Ma da dove deriva questa formula?
Consideriamo il centro della circonferenza e tracciamo i raggi che raggiungono i punti di tangenza con i lati del triangolo. Questi raggi sono perpendicolari ai lati. Possiamo anche tracciare le rette che congiungono il centro della circonferenza con i vertici del triangolo. Queste rette bisecano gli angoli del triangolo equilatero, formando angoli di 30 gradi. A questo punto, possiamo utilizzare le relazioni trigonometriche in un triangolo rettangolo (in particolare, la tangente di 30 gradi) per ricavare la formula sopraindicata. Infatti, metà del lato del triangolo è uguale a r * tan(60°), e tan(60°) = √3.
Calcolare il Raggio Conoscendo il Lato
Se invece conosciamo il lato del triangolo (L) e vogliamo calcolare il raggio della circonferenza (r), possiamo utilizzare la formula inversa:
r = L / (2√3)
Questa formula ci dice che il raggio è uguale al lato del triangolo diviso per due volte la radice quadrata di tre. Possiamo anche razionalizzare il denominatore moltiplicando numeratore e denominatore per √3, ottenendo:
r = (L√3) / 6
Esempi Pratici: Mettiamo in Pratica la Teoria
Per rendere ancora più chiaro il concetto, vediamo alcuni esempi pratici:
Esempio 1: Supponiamo di avere un triangolo equilatero circoscritto a una circonferenza con raggio di 5 cm. Qual è la lunghezza del lato del triangolo?
Utilizzando la formula L = 2√3 * r, otteniamo:
L = 2√3 * 5 = 10√3 cm ≈ 17.32 cm
Quindi, il lato del triangolo è approssimativamente 17.32 cm.
Esempio 2: Supponiamo di avere un triangolo equilatero con lato di 12 cm circoscritto a una circonferenza. Qual è il raggio della circonferenza?
Utilizzando la formula r = L / (2√3), otteniamo:
r = 12 / (2√3) = 6 / √3 = (6√3) / 3 = 2√3 cm ≈ 3.46 cm
Quindi, il raggio della circonferenza è approssimativamente 3.46 cm.
Trucchi e Consigli: Semplificare i Calcoli
Ecco alcuni trucchi e consigli per semplificare i calcoli e risolvere i problemi più facilmente:
- Memorizza le formule: Avere le formule a portata di mano ti farà risparmiare tempo prezioso durante gli esercizi e i compiti in classe.
- Razionalizza i denominatori: Razionalizzare i denominatori può rendere i calcoli più semplici e le risposte più eleganti.
- Utilizza la calcolatrice: Se non sei sicuro dei tuoi calcoli, non esitare a utilizzare una calcolatrice, soprattutto quando hai a che fare con radici quadrate e numeri decimali.
- Disegna il diagramma: Disegnare il diagramma del problema ti aiuterà a visualizzare la situazione e a capire meglio le relazioni tra le diverse grandezze.
Oltre la Geometria: Applicazioni Pratiche
La relazione tra triangoli equilateri e circonferenze non è solo un esercizio teorico di geometria. Ha applicazioni pratiche in diversi campi, tra cui:
- Architettura: La progettazione di strutture con forme geometriche precise richiede una conoscenza approfondita delle relazioni tra diverse figure, inclusi triangoli e circonferenze.
- Ingegneria: Il calcolo di aree e volumi di oggetti con forme complesse spesso richiede la scomposizione degli oggetti in figure geometriche più semplici, come triangoli e circonferenze.
- Design: La creazione di loghi e opere d'arte può beneficiare della conoscenza delle proprietà geometriche di triangoli e circonferenze.
Ad esempio, nella progettazione di una cupola geodetica, la relazione tra il raggio della sfera (che può essere approssimata da una circonferenza in due dimensioni) e i lati dei triangoli che compongono la struttura è cruciale per garantire la stabilità e la resistenza della cupola.
Conclusione: Un Viaggio nella Geometria
Speriamo che questo articolo ti abbia aiutato a comprendere meglio la relazione tra un triangolo equilatero circoscritto a una circonferenza. Abbiamo visto come calcolare il lato del triangolo conoscendo il raggio della circonferenza, e viceversa. Abbiamo anche esplorato alcuni esempi pratici e trucchi per semplificare i calcoli.
La geometria è un campo affascinante e pieno di sorprese. Non aver paura di esplorare, sperimentare e porre domande. Con un po' di impegno e la giusta guida, anche i concetti più complessi possono diventare chiari e accessibili. E ricorda, la matematica è ovunque intorno a noi, basta saperla riconoscere!
Se hai ancora dubbi o domande, non esitare a consultare libri di testo, siti web specializzati o a chiedere aiuto al tuo insegnante di matematica. Buon divertimento con la geometria!