Trapezio Rettangolo Inscritto In Una Circonferenza

L'intersezione tra la geometria e la teoria dei cerchi offre uno scenario affascinante, ricco di teoremi e proprietà uniche. Tra queste configurazioni, il trapezio rettangolo inscritto in una circonferenza spicca per le sue caratteristiche peculiari e le implicazioni che derivano dalla sua particolare costruzione. Questo articolo esplorerà in dettaglio le proprietà di tale trapezio, fornendo una comprensione approfondita delle sue relazioni con la circonferenza circoscritta e presentando alcuni esempi per illustrare la sua rilevanza.
Proprietà Fondamentali del Trapezio Rettangolo Inscritto
Un trapezio è una figura geometrica a quattro lati (un quadrilatero) caratterizzata dall'avere almeno due lati paralleli, che vengono chiamati basi. Un trapezio rettangolo è un trapezio in cui almeno uno dei lati non paralleli (i lati obliqui) è perpendicolare alle basi, formando quindi un angolo retto.
Condizione di Inscrivibilità
Non tutti i quadrilateri possono essere inscritti in una circonferenza. Un quadrilatero può essere inscritto in una circonferenza (cioè essere ciclico) se e solo se i suoi angoli opposti sono supplementari, ovvero se la somma delle loro misure è pari a 180 gradi. Questa è una condizione fondamentale.
Conseguenze per il Trapezio Rettangolo
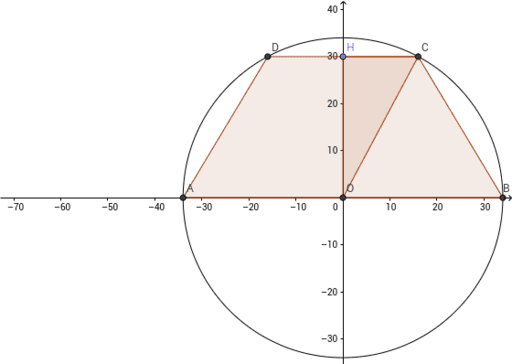
Consideriamo ora un trapezio rettangolo ABCD, con AB e CD come basi parallele e con l'angolo in A retto. Se questo trapezio è inscritto in una circonferenza, allora l'angolo opposto, l'angolo in C, deve essere supplementare ad A. Poiché l'angolo in A è di 90 gradi, l'angolo in C deve anch'esso essere di 90 gradi. Questo significa che il trapezio rettangolo inscritto in una circonferenza ha due angoli retti consecutivi.
Ma questo implica anche qualcosa di molto importante: il lato obliquo AD, che è perpendicolare alle basi, deve coincidere con un diametro della circonferenza. La dimostrazione di questo fatto è relativamente semplice: se AD non fosse un diametro, l'angolo alla circonferenza che insiste su AD (ad esempio, l'angolo in C o in B) non sarebbe necessariamente retto. Poiché abbiamo stabilito che gli angoli in A e C devono essere retti, ne consegue che AD deve essere un diametro.
Relazione tra Lati e Diametro
Una volta stabilito che il lato obliquo perpendicolare alle basi è il diametro della circonferenza, possiamo derivare ulteriori relazioni tra i lati del trapezio e il diametro.
L'Altezza e le Basi
L'altezza del trapezio rettangolo coincide con il diametro della circonferenza. Indichiamo con AB la base maggiore, CD la base minore e AD il diametro. Possiamo quindi dire che AD = 2r, dove r è il raggio della circonferenza.
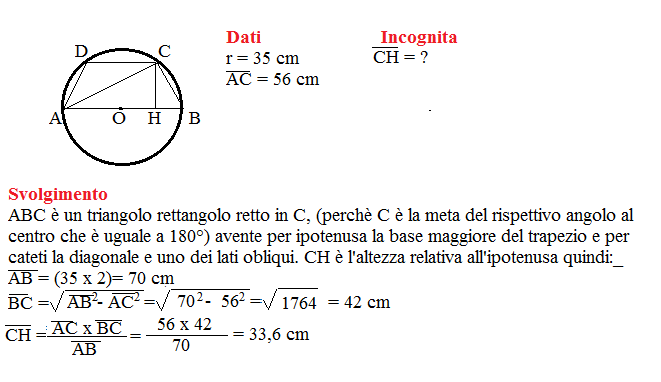
Sia H la proiezione di C sulla base maggiore AB. Il triangolo CHB è rettangolo in H. Inoltre, poiché ABCD è inscritto, possiamo applicare teoremi relativi ai quadrilateri ciclici.
Teorema di Tolomeo
Un teorema utile in questi casi è il teorema di Tolomeo, che afferma che in un quadrilatero ciclico, il prodotto delle diagonali è uguale alla somma dei prodotti dei lati opposti. Applicando questo teorema al nostro trapezio ABCD, otteniamo:
AC * BD = AB * CD + AD * BC
Questo teorema, pur essendo potente, può non essere sempre necessario per risolvere problemi specifici, ma offre una prospettiva interessante sulla relazione tra i lati e le diagonali.
Calcolo dell'Area
L'area di un trapezio è data dalla formula:
Area = (Base Maggiore + Base Minore) * Altezza / 2
Nel nostro caso, l'altezza coincide con il diametro della circonferenza. Pertanto:
Area = (AB + CD) * (2r) / 2 = (AB + CD) * r
Questo significa che per calcolare l'area del trapezio rettangolo inscritto, è sufficiente conoscere la somma delle basi e il raggio della circonferenza.
Esempi Pratici
Consideriamo un trapezio rettangolo ABCD inscritto in una circonferenza di raggio 5 cm. Supponiamo che la base maggiore AB misuri 8 cm e la base minore CD misuri 2 cm. Calcoliamo l'area del trapezio.
L'area è data da:
Area = (8 + 2) * 5 = 50 cm²
Ora, proviamo a calcolare la lunghezza del lato obliquo BC. Sappiamo che AD è il diametro e misura 10 cm. Possiamo utilizzare il teorema di Pitagora nel triangolo rettangolo CHB, dove CH = AD = 10 cm e HB = AB - AH = AB - CD = 8 - 2 = 6 cm.
Pertanto, BC = √(CH² + HB²) = √(10² + 6²) = √(100 + 36) = √136 ≈ 11.66 cm
Un altro esempio potrebbe essere la progettazione di un palco per un evento. Immagina di voler creare un palco a forma di trapezio rettangolo che sia inscritto in un'area circolare delimitata da transenne. Conoscendo il raggio dell'area circolare e la lunghezza desiderata per la base maggiore del palco, puoi utilizzare le proprietà del trapezio rettangolo inscritto per determinare le dimensioni precise della base minore e del lato obliquo, assicurandoti che il palco si adatti perfettamente allo spazio disponibile.
Applicazioni e Considerazioni Aggiuntive
La comprensione delle proprietà del trapezio rettangolo inscritto in una circonferenza non è solo un esercizio teorico. Trova applicazioni in diversi campi, tra cui:
- Architettura: Nella progettazione di strutture che combinano elementi circolari e rettilinei.
- Ingegneria: Nel calcolo di aree e volumi in contesti geometrici specifici.
- Grafica Computerizzata: Nella modellazione 3D e nella creazione di forme complesse.
- Ottica: Nella progettazione di lenti e specchi con forme particolari.
È importante sottolineare che la condizione di inscrivibilità è cruciale. Se un trapezio rettangolo non soddisfa questa condizione, le proprietà discusse in questo articolo non si applicano.
Conclusioni
Il trapezio rettangolo inscritto in una circonferenza è una figura geometrica affascinante che presenta proprietà uniche e derivanti dalla sua particolare costruzione. La condizione fondamentale che lo caratterizza è che il lato obliquo perpendicolare alle basi coincide con il diametro della circonferenza circoscritta. Da questa condizione derivano importanti relazioni tra i lati, le diagonali, l'area e il raggio della circonferenza. La comprensione di queste proprietà può essere utile in diversi contesti, dalla risoluzione di problemi geometrici alla progettazione di strutture complesse.
Invitiamo il lettore a esplorare ulteriormente questo argomento, risolvendo esercizi specifici e approfondendo la conoscenza dei teoremi relativi ai quadrilateri ciclici. La geometria è un campo vasto e affascinante, e la scoperta delle relazioni che legano le diverse figure geometriche è un'esperienza gratificante e stimolante.