Trapezio Isoscele Circoscritto A Una Semicirconferenza

Ti sei mai trovato di fronte a un problema di geometria che sembrava un vero e proprio labirinto? Magari un trapezio isoscele, circoscritto a una semicirconferenza, e ti sei chiesto da dove cominciare? Non sei solo. Molti studenti (e anche professionisti!) si scontrano con figure geometriche complesse come questa. Cerchiamo di dipanare questa matassa insieme, in modo chiaro e pratico.

In questo articolo, esploreremo a fondo il trapezio isoscele circoscritto a una semicirconferenza. Non ci limiteremo a definizioni teoriche, ma ci concentreremo su come risolvere problemi, quali proprietà utilizzare e, soprattutto, come visualizzare la figura per semplificare il ragionamento. Pronti a partire?

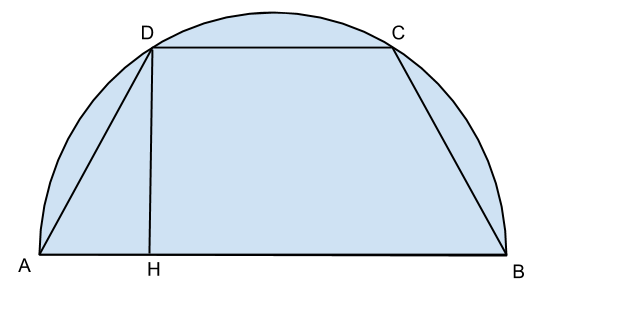
Cos'è un Trapezio Isoscele Circoscritto a una Semicirconferenza?

Partiamo dalle basi. Un trapezio è un quadrilatero con almeno due lati paralleli, chiamati basi. In un trapezio isoscele, i lati non paralleli (i lati obliqui) sono congruenti, ovvero hanno la stessa lunghezza.

Ora, cosa significa che un trapezio è circoscritto a una semicirconferenza? Vuol dire che la semicirconferenza è interna al trapezio e che tutti e quattro i lati del trapezio sono tangenti alla semicirconferenza. Immagina una mezza luna racchiusa perfettamente all'interno di un trapezio, toccando tutti i suoi bordi.

Proprietà Fondamentali

La chiave per risolvere problemi con i trapezi isosceli circoscritti a una semicirconferenza risiede nelle loro proprietà. Eccone alcune essenziali:

Somma delle Basi = Somma dei Lati Obliqui: In un quadrilatero circoscritto a una circonferenza (e quindi anche a una semicirconferenza), la somma dei lati opposti è uguale. Nel nostro caso, la somma della base maggiore (B) e della base minore (b) è uguale alla somma dei due lati obliqui (l). Quindi: B + b = l + l = 2l
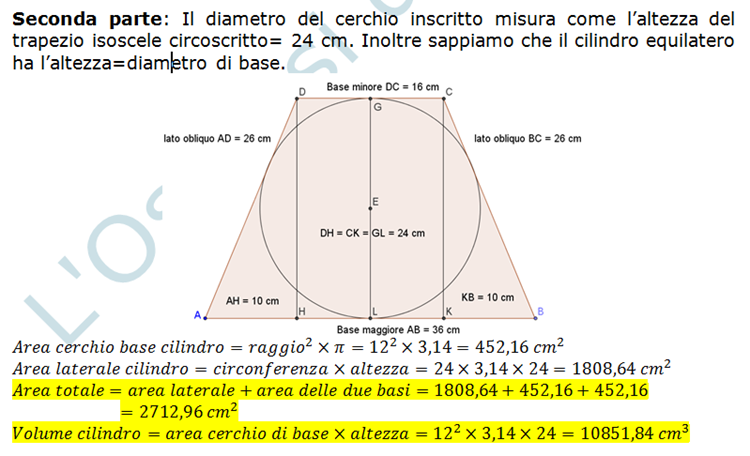
Altezza = Diametro: L'altezza del trapezio, che è la distanza perpendicolare tra le due basi, è uguale al diametro della semicirconferenza. Questo è un punto cruciale per collegare la figura alla circonferenza.
Angoli alla Base: Gli angoli alla base maggiore del trapezio sono congruenti, così come gli angoli alla base minore. Questo deriva dalla proprietà di essere un trapezio isoscele.
Raggio e Tangenza: Il raggio della semicirconferenza, tracciato dal centro fino al punto di tangenza con un lato del trapezio, è perpendicolare a quel lato. Questa proprietà crea angoli retti, utilissimi per applicare il teorema di Pitagora o le funzioni trigonometriche.

Come Affrontare i Problemi: Un Approccio Pratico

Ok, teoria a posto. Ma come tradurre tutto questo in pratica? Vediamo un approccio passo-passo per affrontare i problemi:

Disegna la Figura: Un disegno preciso è fondamentale. Disegna il trapezio isoscele e la semicirconferenza interna, facendo attenzione a rappresentare i punti di tangenza.
Identifica le Informazioni Date: Leggi attentamente il problema e segna sul disegno tutte le informazioni fornite: lunghezze dei lati, angoli, raggio della semicirconferenza, ecc.
Applica le Proprietà: Sfrutta le proprietà che abbiamo elencato. Ad esempio, se conosci la lunghezza dei lati obliqui, sai che la somma delle basi è il doppio di quella lunghezza. Se conosci il raggio, conosci l'altezza del trapezio.
Costruisci Triangoli Rettangoli: Spesso, tracciare l'altezza del trapezio dal vertice della base minore alla base maggiore ti permette di creare triangoli rettangoli. In questi triangoli, puoi applicare il teorema di Pitagora o le funzioni trigonometriche (seno, coseno, tangente) per trovare lunghezze o angoli mancanti.
Utilizza il Teorema di Pitagora: Molto spesso è il tuo migliore amico. Nei triangoli rettangoli che si formano, puoi correlare i lati (ipotenusa, cateto maggiore, cateto minore) con la formula a² + b² = c².
Risolvi il Sistema di Equazioni (se necessario): A volte, avrai bisogno di impostare un sistema di equazioni per trovare le incognite. Ricorda che ogni proprietà e ogni relazione geometrica possono essere tradotte in un'equazione.

Esempio Pratico:

Immagina un trapezio isoscele circoscritto a una semicirconferenza. La base maggiore misura 10 cm e il lato obliquo 6 cm. Calcola la base minore.

Soluzione:

Disegno: Disegna la figura.
Informazioni Date: B = 10 cm, l = 6 cm.
Applica le Proprietà: Sappiamo che B + b = 2l. Quindi, 10 + b = 2 * 6 = 12.
Risolvi: b = 12 - 10 = 2 cm.

Quindi la base minore misura 2 cm.

Errori Comuni da Evitare

Anche i geometri più esperti a volte commettono errori. Ecco alcuni errori comuni da evitare quando si lavora con i trapezi isosceli circoscritti a una semicirconferenza:

Confondere le proprietà del trapezio isoscele con quelle di un trapezio generico: Ricorda che solo nel trapezio isoscele i lati obliqui sono congruenti e gli angoli alla base sono uguali.
Dimenticare che l'altezza è uguale al diametro: Questa è una relazione fondamentale che semplifica molti problemi.
Non sfruttare i punti di tangenza: I punti di tangenza creano angoli retti e relazioni geometriche che possono essere utili.
Non fare un disegno preciso: Un disegno impreciso può portare a errori di ragionamento.
Non considerare le unità di misura: Assicurati che tutte le lunghezze siano espresse nella stessa unità di misura prima di effettuare i calcoli.

Perché è Utile Conoscere Questi Concetti?

Potresti chiederti: "Ok, bello, ma a cosa mi serve tutto questo nella vita reale?". La geometria, e in particolare la comprensione di figure come il trapezio isoscele circoscritto a una semicirconferenza, sviluppa il pensiero logico e la capacità di risolvere problemi. Queste abilità sono preziose in molti campi, dall'ingegneria all'architettura, dalla programmazione alla finanza. Inoltre, la geometria è alla base di molte tecnologie, come la grafica computerizzata e la realtà virtuale.

Ma c'è di più. Comprendere la geometria significa allenare la mente a vedere relazioni e pattern. Significa imparare a scomporre problemi complessi in parti più semplici e a trovare soluzioni creative. E questo è un'abilità preziosa in qualsiasi ambito della vita.

Consigli Avanzati

Se hai padronanza delle basi, ecco alcuni consigli per affrontare problemi più complessi:

Considera l'area del trapezio: L'area del trapezio si calcola come (B + b) * h / 2, dove B è la base maggiore, b è la base minore e h è l'altezza. A volte, conoscere l'area può aiutarti a trovare altre informazioni mancanti.
Utilizza la trigonometria in modo avanzato: Se hai a che fare con angoli particolari (30°, 45°, 60°), puoi utilizzare le relazioni trigonometriche notevoli per semplificare i calcoli.
Esplora le relazioni tra il trapezio e la circonferenza circoscritta (se esiste): Anche se il trapezio è circoscritto *a una semicirconferenza*, potresti trovarti in situazioni in cui è circoscrivibile ad una *circonferenza completa*. Studiare le proprietà della circonferenza circoscritta può fornire nuove prospettive e strumenti di risoluzione.

Conclusione

Il trapezio isoscele circoscritto a una semicirconferenza può sembrare un problema ostico all'inizio, ma con la giusta conoscenza delle proprietà e un approccio metodico, può essere affrontato con successo. Ricorda di disegnare la figura, identificare le informazioni date, applicare le proprietà fondamentali e costruire triangoli rettangoli. Non aver paura di sperimentare e di utilizzare il teorema di Pitagora e le funzioni trigonometriche. E soprattutto, non arrenderti di fronte alle difficoltà. La geometria è un viaggio di scoperta, e ogni problema risolto è un passo avanti verso la comprensione del mondo che ci circonda.

Spero che questo articolo ti sia stato utile. Ora tocca a te: prendi un libro di geometria, scegli un problema con un trapezio isoscele circoscritto a una semicirconferenza e mettiti alla prova. Buon lavoro!