Terzo Criterio Di Congruenza Dei Triangoli Rettangoli

Capita spesso, studiando geometria, di sentirsi un po' persi di fronte a teoremi e criteri. E la geometria, lo sappiamo bene, è ovunque intorno a noi! Dalla forma dei nostri edifici, al design dei nostri smartphone, fino alla semplice suddivisione di una pizza. Comprendere i principi fondamentali della geometria, come i criteri di congruenza dei triangoli, ci aiuta a decifrare il mondo che ci circonda e a risolvere problemi pratici. Oggi ci concentriamo su un criterio specifico, il Terzo Criterio di Congruenza dei Triangoli Rettangoli, cercando di renderlo il più chiaro e accessibile possibile.

Cosa significa "Congruenza"?

Prima di addentrarci nel criterio specifico, è fondamentale capire cosa significa che due figure geometriche sono congruenti. Semplicemente, due figure sono congruenti se, sovrapponendole, coincidono perfettamente. Immaginate di avere due ritagli di carta identici; se li sovrapponete, non noterete alcuna differenza. Ecco, quelli sono congruenti. Per i triangoli, la congruenza significa che tutti e tre i lati e tutti e tre gli angoli corrispondenti sono uguali.

I Criteri di Congruenza dei Triangoli: Un Recap Veloce

Esistono diversi criteri che ci permettono di stabilire se due triangoli sono congruenti senza dover misurare ogni singolo lato e angolo. Ricordiamoli brevemente:

Primo Criterio (LAL): Se due triangoli hanno due lati e l'angolo tra essi compreso congruenti, allora i triangoli sono congruenti.
Secondo Criterio (ALA o LAA): Se due triangoli hanno due angoli e il lato tra essi compreso congruenti, oppure due angoli e un lato non compreso congruenti, allora i triangoli sono congruenti.
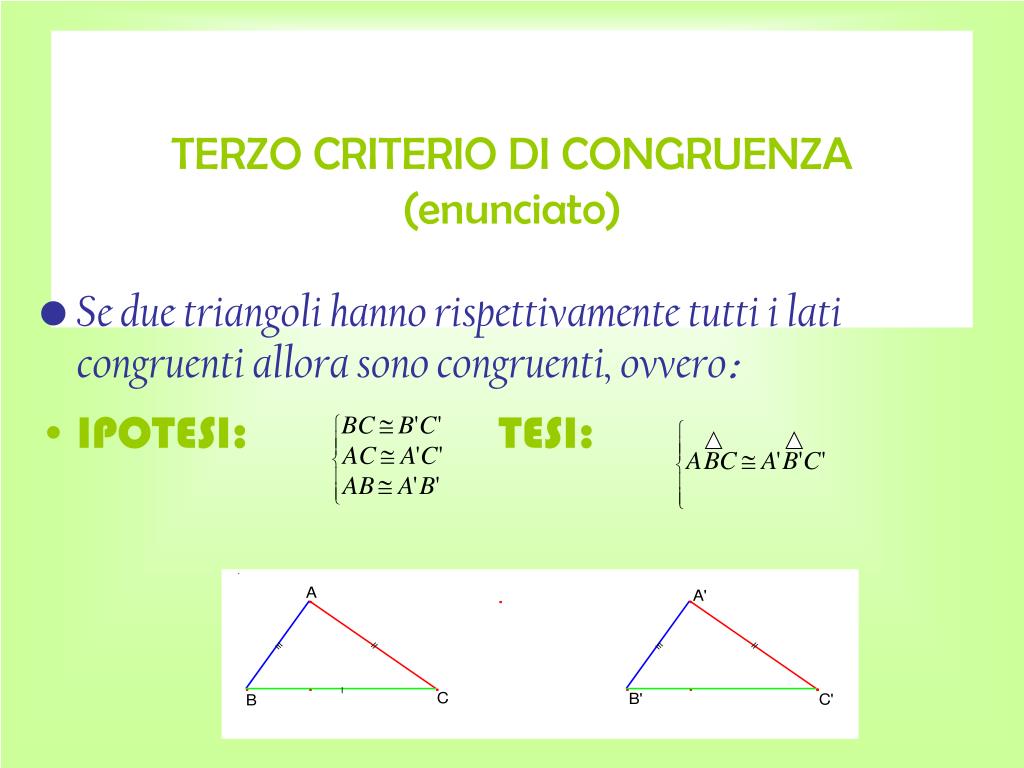
Terzo Criterio (LLL): Se due triangoli hanno tutti e tre i lati congruenti, allora i triangoli sono congruenti.

Questi criteri sono validi per *tutti* i tipi di triangoli. Ma i triangoli rettangoli, grazie alla presenza dell'angolo retto (90 gradi), godono di criteri di congruenza specifici, che semplificano ulteriormente la verifica.

Il Cuore del Problema: Il Terzo Criterio di Congruenza dei Triangoli Rettangoli

Ed eccoci al punto cruciale: il Terzo Criterio di Congruenza dei Triangoli Rettangoli. Questo criterio afferma:

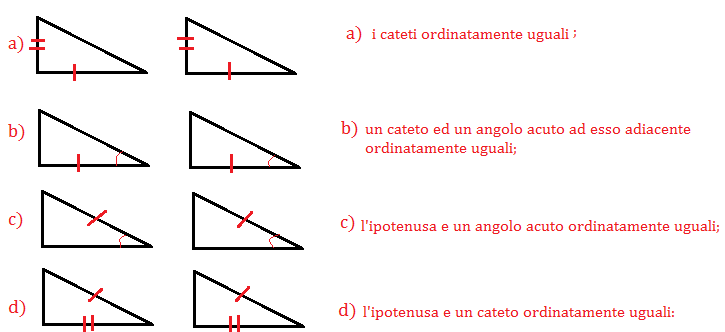
"Se due triangoli rettangoli hanno un cateto e l'ipotenusa rispettivamente congruenti, allora sono congruenti."

Cerchiamo di scomporre questa affermazione:

* Triangoli Rettangoli: Sono triangoli che hanno un angolo di 90 gradi (angolo retto). * Cateto: È uno dei due lati che formano l'angolo retto. Un triangolo rettangolo ha due cateti. * Ipotenusa: È il lato opposto all'angolo retto, ed è anche il lato più lungo del triangolo rettangolo.

Quindi, se prendiamo due triangoli rettangoli e verifichiamo che un cateto del primo triangolo è uguale a un cateto del secondo triangolo, e l'ipotenusa del primo triangolo è uguale all'ipotenusa del secondo triangolo, allora possiamo concludere, senza ulteriori misurazioni, che i due triangoli sono congruenti.

Perché Funziona? Una Dimostrazione Intuitiva

La validità di questo criterio può essere compresa ricorrendo al Teorema di Pitagora. Ricordiamo che il Teorema di Pitagora afferma che, in un triangolo rettangolo, il quadrato costruito sull'ipotenusa è uguale alla somma dei quadrati costruiti sui cateti (a² + b² = c²).

Supponiamo di avere due triangoli rettangoli, chiamiamoli ABC e A'B'C', dove C e C' sono gli angoli retti. Sappiamo che:

* AC = A'C' (un cateto è congruente) * AB = A'B' (l'ipotenusa è congruente)

Applichiamo il Teorema di Pitagora a entrambi i triangoli:

* In ABC: AC² + BC² = AB² * In A'B'C': A'C'² + B'C'² = A'B'²

Poiché AC = A'C' e AB = A'B', possiamo sostituire nella seconda equazione:

* (AC)² + B'C'² = (AB)²

Sottraendo (AC)² da entrambi i lati dell'equazione, otteniamo:

* B'C'² = (AB)² - (AC)²

Ma (AB)² - (AC)² è proprio BC² (dalla prima equazione). Quindi:

* B'C'² = BC²

Prendendo la radice quadrata di entrambi i lati, otteniamo:

* BC = B'C'

Abbiamo dimostrato che anche il secondo cateto è congruente. Ora sappiamo che i due triangoli hanno tutti e tre i lati congruenti (AC = A'C', AB = A'B' e BC = B'C'). Per il Terzo Criterio di Congruenza dei Triangoli (LLL), possiamo concludere che i triangoli ABC e A'B'C' sono congruenti.

Esempio Pratico

Immaginate di dover costruire due rampe identiche per skateboard. Avete due assi di legno. Sapete che l'angolo tra la base e la verticale deve essere di 90 gradi. Misurate la lunghezza di una delle assi che farà da base (cateto) e la lunghezza dell'asse diagonale (ipotenusa). Se queste due misure corrispondono esattamente per entrambe le rampe, potete essere certi che le rampe saranno esattamente identiche, anche se non avete misurato l'altezza verticale.

Critiche e Alternative

Alcuni potrebbero obiettare che l'utilizzo del Teorema di Pitagora per dimostrare questo criterio rende, in un certo senso, il criterio stesso ridondante. In fondo, se conosciamo due lati di un triangolo rettangolo, possiamo sempre calcolare il terzo lato usando Pitagora e poi applicare il criterio LLL. Questa obiezione è valida, ma il Terzo Criterio di Congruenza dei Triangoli Rettangoli offre comunque una scorciatoia, un metodo più diretto, che in determinate situazioni può risultare più pratico e veloce.

Un'altra alternativa, meno formale ma ugualmente valida, è pensare alla costruzione del triangolo. Se si fissa la lunghezza di un cateto e dell'ipotenusa, esiste una sola possibile lunghezza per l'altro cateto (determinata dal Teorema di Pitagora). Pertanto, esiste un solo triangolo rettangolo possibile con quelle due caratteristiche, garantendo la congruenza.

L'Importanza di Comprendere i Criteri di Congruenza

La comprensione dei criteri di congruenza, incluso il Terzo Criterio per i triangoli rettangoli, è fondamentale per diverse ragioni:

* Risoluzione di Problemi Geometrici: Sono strumenti essenziali per dimostrare teoremi e risolvere problemi di geometria. * Applicazioni Pratiche: Trovano impiego in architettura, ingegneria, design e in molte altre discipline. * Sviluppo del Ragionamento Logico: Aiutano a sviluppare il pensiero critico e la capacità di ragionamento deduttivo. * Fondamenta per Concetti Più Avanzati: Sono la base per lo studio di argomenti più complessi, come la trigonometria e la geometria analitica.

In Sintesi

Il Terzo Criterio di Congruenza dei Triangoli Rettangoli è un potente strumento che ci permette di affermare la congruenza di due triangoli rettangoli conoscendo solamente la lunghezza di un cateto e dell'ipotenusa. Semplifica la risoluzione di problemi e fornisce una base solida per lo studio della geometria.

Un Ultimo Pensiero

La prossima volta che vi trovate di fronte a una figura geometrica, provate a scomporla in triangoli. Chiedetevi se potete applicare i criteri di congruenza per risolvere un problema o semplicemente per capire meglio la sua struttura. La geometria è un linguaggio, e imparare a parlarlo significa acquisire una nuova prospettiva sul mondo che ci circonda.

Vi siete mai trovati a utilizzare inconsapevolmente i criteri di congruenza nella vita di tutti i giorni? Riflettete su come questi concetti, apparentemente astratti, si manifestano concretamente nella vostra esperienza.