Teorema Del Seno E Del Coseno

La trigonometria è un ramo fondamentale della matematica che studia le relazioni tra gli angoli e i lati dei triangoli. Due strumenti potenti in questo campo sono il Teorema del Seno e il Teorema del Coseno. Questi teoremi permettono di risolvere triangoli, ovvero di trovare le misure di tutti i loro angoli e lati, conoscendo solo alcune informazioni. In questo articolo, esploreremo in dettaglio questi teoremi, le loro applicazioni e forniremo esempi pratici.

Teorema del Seno

Definizione e Formula

Il Teorema del Seno afferma che, in un triangolo qualsiasi, il rapporto tra la lunghezza di un lato e il seno dell'angolo opposto è costante. Matematicamente, per un triangolo ABC con lati a, b, c e angoli α, β, γ rispettivamente opposti a tali lati, il teorema è espresso come:

a / sin(α) = b / sin(β) = c / sin(γ)

In altre parole, possiamo dire che il rapporto tra lato e seno dell'angolo opposto è lo stesso per tutti i lati e angoli del triangolo. Questo è un concetto chiave per capire e applicare il teorema.

Condizioni di Applicabilità

Il Teorema del Seno è particolarmente utile quando si conoscono le seguenti informazioni di un triangolo:

* Due angoli e un lato (AAS o ASA): Se conosciamo due angoli e un lato qualsiasi, possiamo trovare gli altri lati usando il Teorema del Seno. * Due lati e un angolo opposto a uno di essi (SSA): Questa configurazione è nota come il caso ambiguo, perché può portare a nessuna, una o due soluzioni possibili. Bisogna fare attenzione nell'interpretazione dei risultati.

Esempio di Applicazione

Supponiamo di avere un triangolo ABC dove l'angolo α = 30°, l'angolo β = 45° e il lato a = 10 cm. Vogliamo trovare la lunghezza del lato b.

Utilizzando il Teorema del Seno:

a / sin(α) = b / sin(β)

Sostituendo i valori noti:

10 / sin(30°) = b / sin(45°)

Poiché sin(30°) = 0.5 e sin(45°) = √2 / 2, otteniamo:

10 / 0.5 = b / (√2 / 2)

20 = b / (√2 / 2)

b = 20 * (√2 / 2) = 10√2 ≈ 14.14 cm

Quindi, la lunghezza del lato b è approssimativamente 14.14 cm.

Teorema del Coseno

Definizione e Formula

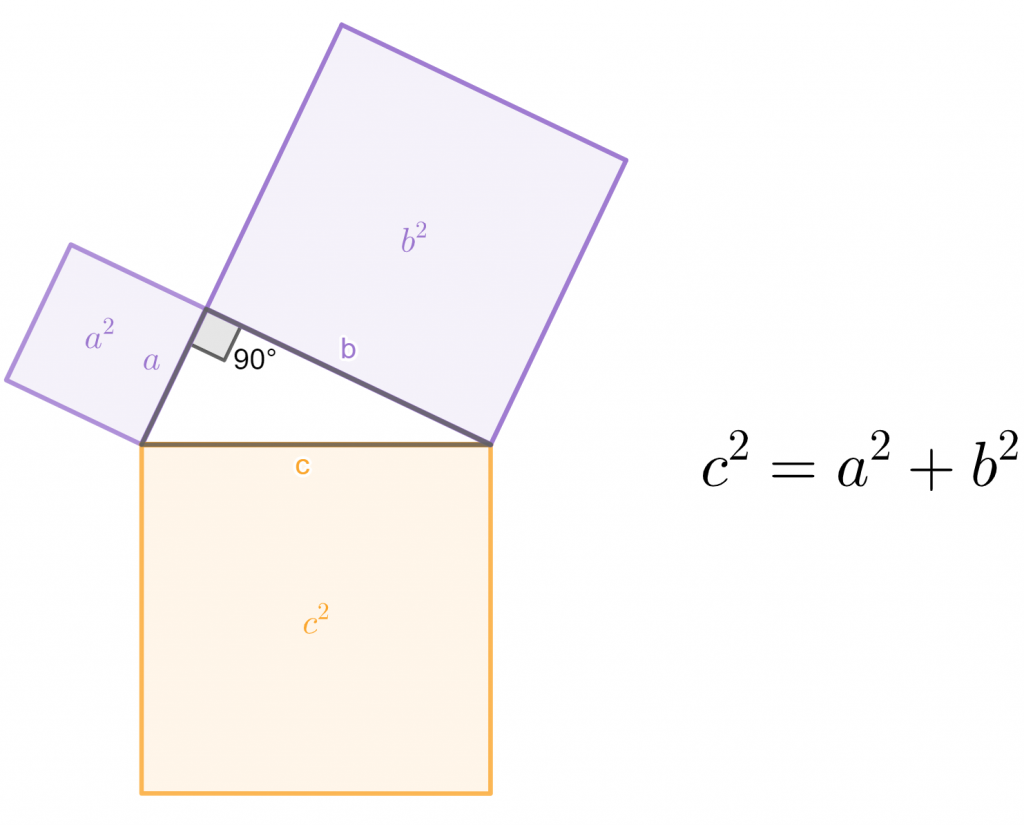
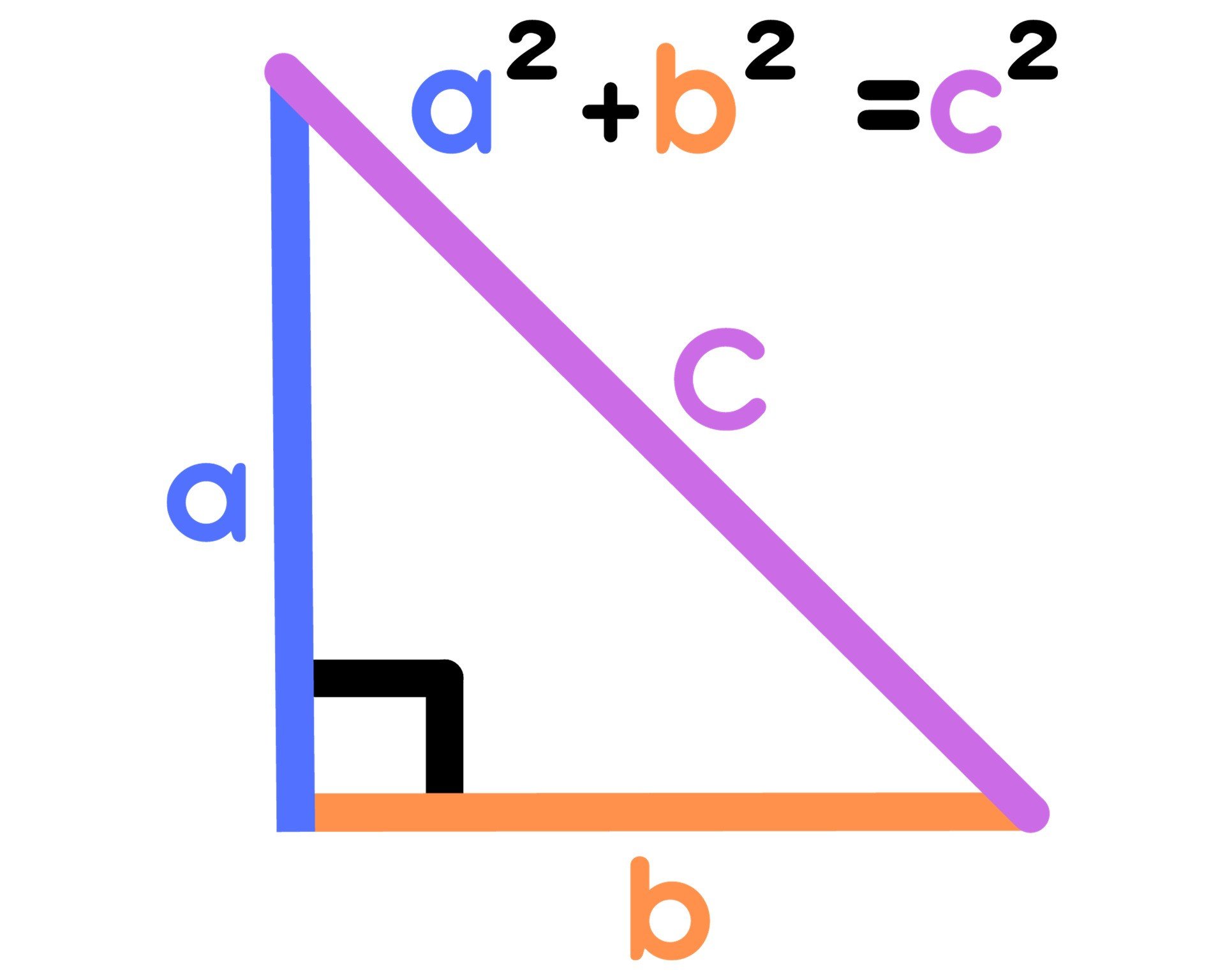
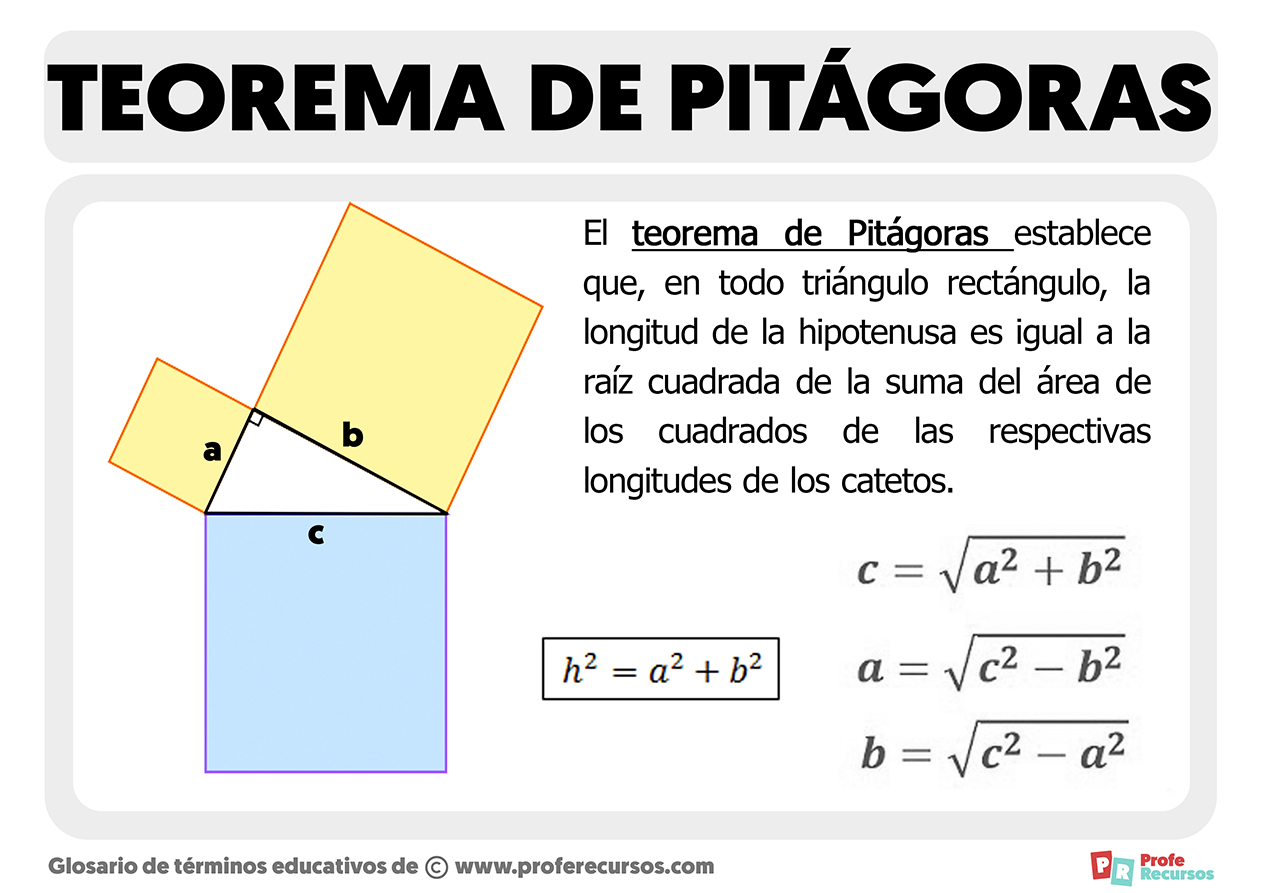
Il Teorema del Coseno è una generalizzazione del teorema di Pitagora. Afferma che, in un triangolo qualsiasi, il quadrato di un lato è uguale alla somma dei quadrati degli altri due lati meno il doppio del prodotto di questi due lati per il coseno dell'angolo compreso tra loro. Per un triangolo ABC con lati a, b, c e angoli α, β, γ rispettivamente opposti a tali lati, il teorema è espresso come:

* a² = b² + c² - 2bc * cos(α) * b² = a² + c² - 2ac * cos(β) * c² = a² + b² - 2ab * cos(γ)

È importante notare che se l'angolo α è un angolo retto (90°), allora cos(α) = 0, e la formula si riduce al teorema di Pitagora: a² = b² + c².

Condizioni di Applicabilità

Il Teorema del Coseno è particolarmente utile quando si conoscono le seguenti informazioni di un triangolo:

* Tre lati (SSS): Se conosciamo la lunghezza di tutti i tre lati, possiamo trovare tutti gli angoli usando il Teorema del Coseno. * Due lati e l'angolo compreso (SAS): Se conosciamo la lunghezza di due lati e l'angolo tra di essi, possiamo trovare il terzo lato usando il Teorema del Coseno.

Esempio di Applicazione

Supponiamo di avere un triangolo ABC dove il lato a = 5 cm, il lato b = 7 cm e l'angolo γ = 60°. Vogliamo trovare la lunghezza del lato c.

Utilizzando il Teorema del Coseno:

c² = a² + b² - 2ab * cos(γ)

Sostituendo i valori noti:

c² = 5² + 7² - 2 * 5 * 7 * cos(60°)

Poiché cos(60°) = 0.5, otteniamo:

c² = 25 + 49 - 70 * 0.5

c² = 74 - 35

c² = 39

c = √39 ≈ 6.25 cm

Quindi, la lunghezza del lato c è approssimativamente 6.25 cm.

Applicazioni nel Mondo Reale

I Teoremi del Seno e del Coseno non sono solo strumenti teorici, ma hanno numerose applicazioni pratiche in diversi campi:

* Navigazione: Utilizzati per calcolare distanze e rotte in navigazione marittima e aerea. Ad esempio, per calcolare la distanza tra due punti su una mappa conoscendo gli angoli e le distanze parziali. * Architettura e Ingegneria: Utilizzati per progettare strutture, calcolare angoli e lunghezze in costruzioni, ponti e altre opere ingegneristiche. Per esempio, per calcolare l'inclinazione di un tetto o la lunghezza di una trave. * Agrimensura: Utilizzati per misurare terreni e calcolare aree. Permettono di determinare le dimensioni di un lotto di terreno anche se non è perfettamente rettangolare o quadrato. * Fisica: Utilizzati per risolvere problemi di meccanica, ottica e altre aree della fisica. Ad esempio, per calcolare la risultante di due forze che agiscono su un corpo. * Astronomia: Utilizzati per calcolare distanze tra stelle e pianeti. La parallasse, un metodo di misurazione delle distanze stellari, si basa su principi trigonometrici.

Esempio Reale: Calcolo dell'Altezza di una Montagna

Un esempio classico è il calcolo dell'altezza di una montagna. Supponiamo di trovarci a una certa distanza dalla base di una montagna e di misurare l'angolo di elevazione della cima. Poi, ci spostiamo di una certa distanza e misuriamo di nuovo l'angolo di elevazione. Utilizzando il Teorema del Seno, possiamo impostare un sistema di equazioni e risolvere per l'altezza della montagna. Questa tecnica è usata in geodesia e in cartografia.

Immaginiamo di misurare un angolo di elevazione di 35 gradi da un punto A. Ci allontaniamo di 100 metri fino a un punto B e misuriamo un angolo di elevazione di 28 gradi. Possiamo utilizzare il teorema del seno per calcolare l'altezza della montagna. Questo problema si traduce nella risoluzione di un triangolo dove conosciamo un lato (la distanza di 100 metri) e due angoli.

Conclusioni

Il Teorema del Seno e il Teorema del Coseno sono strumenti essenziali per la risoluzione di triangoli e hanno una vasta gamma di applicazioni pratiche. Comprendere questi teoremi e saperli applicare correttamente è fondamentale per chiunque studi matematica, fisica, ingegneria o qualsiasi campo che richieda la risoluzione di problemi geometrici. La loro versatilità li rende indispensabili per affrontare sfide reali che coinvolgono angoli e distanze.

Per approfondire la tua conoscenza di questi teoremi, ti consiglio di esercitarti con diversi esercizi, esplorare le dimostrazioni matematiche dei teoremi e cercare applicazioni pratiche nel tuo campo di interesse. La comprensione approfondita di questi concetti aprirà nuove porte alla risoluzione di problemi complessi e alla comprensione del mondo che ci circonda. Non smettere mai di esplorare e di applicare queste conoscenze!