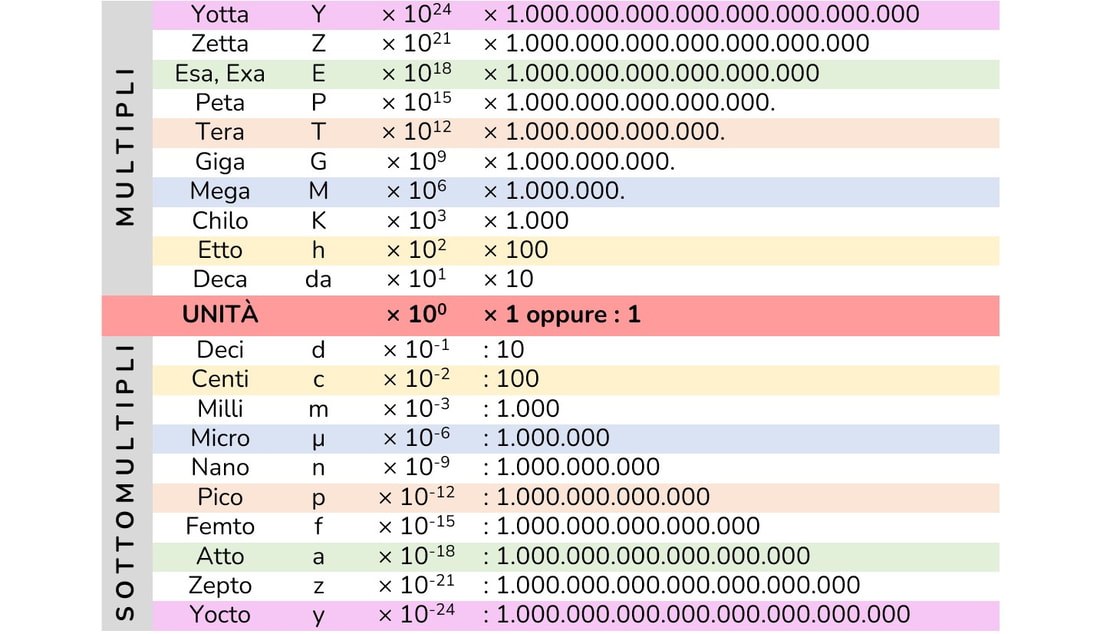
Tabella Dei Grammi Multipli E Sottomultipli

La comprensione del Sistema Internazionale di Unità di Misura (SI) è fondamentale in una vasta gamma di discipline, dalla scienza all'ingegneria, passando per la cucina e il commercio. Un aspetto cruciale di questo sistema è la capacità di esprimere quantità molto grandi o molto piccole utilizzando multipli e sottomultipli dell'unità base. Questi prefissi, combinati con l'unità di misura, ci permettono di manipolare facilmente numeri di ordini di grandezza significativamente diversi, semplificando calcoli e comunicazioni. Questa guida esplorerà in dettaglio la tabella dei grammi multipli e sottomultipli, illustrandone l'importanza e fornendo esempi pratici del suo utilizzo.

Importanza della Tabella dei Multipli e Sottomultipli

La tabella dei multipli e sottomultipli non si limita al grammo; è un concetto applicabile a tutte le unità di misura del SI, come metri, litri, secondi, ampere e così via. La sua importanza risiede nella sua capacità di:

• Semplificare la notazione: Evita di scrivere numeri con molti zeri, rendendo la lettura e la comprensione più immediate.
• Facilitare i calcoli: Permette di lavorare con numeri più maneggevoli, riducendo il rischio di errori.
• Standardizzare le comunicazioni: Assicura che le misurazioni siano interpretate correttamente da persone di diverse provenienze e con diversi background.
• Rappresentare accuratamente grandezze diverse: Permette di esprimere valori sia infinitamente piccoli che enormemente grandi con la stessa precisione e facilità.

Comprendere la Struttura della Tabella

La tabella dei multipli e sottomultipli è organizzata attorno all'unità base (in questo caso, il grammo, simbolo g). I multipli rappresentano valori maggiori dell'unità base, mentre i sottomultipli rappresentano valori minori. Ogni prefisso è associato a un fattore di moltiplicazione specifico, che è una potenza di 10.

I prefissi sono derivati principalmente dal greco e dal latino. Ad esempio, "kilo" deriva dal greco "chilioi," che significa mille, mentre "milli" deriva dal latino "mille," che significa anche mille, ma in riferimento a una frazione.

La Tabella dei Multipli del Grammo

I multipli del grammo, che rappresentano pesi superiori al grammo, sono i seguenti (elenco parziale, considerando i più comuni):

• decagrammo (dag): 1 dag = 10 g
• ettogrammo (hg): 1 hg = 100 g
• chilogrammo (kg): 1 kg = 1000 g
• megagrammo (Mg): 1 Mg = 1.000.000 g (anche noto come tonnellata)

Notare che ogni prefisso rappresenta un aumento di un fattore di 10 rispetto al precedente (o un fattore di 1000, nel caso di alcuni salti, come da kg a Mg).

Esempi di Utilizzo dei Multipli del Grammo

Vediamo alcuni esempi concreti:

• Acquisto di frutta e verdura: Spesso al mercato si acquistano chilogrammi (kg) di mele, patate o arance. Un chilogrammo corrisponde a 1000 grammi.
• Peso di un sacco di cemento: Un sacco di cemento può pesare 25 chilogrammi (kg), che equivalgono a 25.000 grammi.
• Peso di un'automobile: Il peso di un'automobile viene spesso espresso in tonnellate (ton), che sono equivalenti a megagrammi (Mg). Ad esempio, un'automobile può pesare 1.5 tonnellate, equivalenti a 1.5 Mg o 1.500.000 grammi.
• Ricette di cucina: Anche se spesso si usano i grammi, alcune ricette che richiedono grandi quantità di ingredienti (come preparare una torta per molte persone) potrebbero indicare la quantità di zucchero in ettogrammi (hg).

La Tabella dei Sottomultipli del Grammo

I sottomultipli del grammo, che rappresentano pesi inferiori al grammo, sono i seguenti (elenco parziale, considerando i più comuni):

• decigrammo (dg): 1 dg = 0.1 g
• centigrammo (cg): 1 cg = 0.01 g
• milligrammo (mg): 1 mg = 0.001 g
• microgrammo (µg): 1 µg = 0.000001 g

Analogamente ai multipli, ogni prefisso rappresenta una diminuzione di un fattore di 10 rispetto al precedente (o un fattore di 1000 in alcuni salti, come da mg a µg).

Esempi di Utilizzo dei Sottomultipli del Grammo

I sottomultipli del grammo sono particolarmente importanti in contesti dove la precisione è fondamentale, come:

• Medicina: Le dosi dei farmaci sono spesso espresse in milligrammi (mg). Ad esempio, una compressa di paracetamolo può contenere 500 mg di principio attivo.
• Chimica: Nelle analisi chimiche, la concentrazione di sostanze può essere espressa in microgrammi (µg) per litro (µg/L).
• Oreficeria: La purezza dell'oro viene spesso misurata utilizzando i milligrammi (mg), soprattutto quando si parla di placcature sottili.
• Alimentazione: L'etichettatura degli alimenti spesso indica il contenuto di vitamine e minerali in milligrammi (mg) o talvolta anche in microgrammi (µg).

Conversioni tra Multipli e Sottomultipli

La capacità di convertire tra diversi multipli e sottomultipli è essenziale. Ecco alcune regole generali:

• Per convertire da un'unità più grande a una più piccola: Moltiplicare per la potenza di 10 appropriata. Ad esempio, per convertire chilogrammi in grammi, moltiplicare per 1000 (1 kg = 1000 g).
• Per convertire da un'unità più piccola a una più grande: Dividere per la potenza di 10 appropriata. Ad esempio, per convertire milligrammi in grammi, dividere per 1000 (1 mg = 0.001 g).

È utile visualizzare la tabella dei prefissi come una scala. Salendo la scala (verso multipli più grandi), si divide; scendendo la scala (verso sottomultipli più piccoli), si moltiplica.

Esempio di Conversione

Convertire 3.5 chilogrammi (kg) in milligrammi (mg):

1. Prima convertiamo i chilogrammi in grammi: 3.5 kg * 1000 g/kg = 3500 g
2. Poi convertiamo i grammi in milligrammi: 3500 g * 1000 mg/g = 3.500.000 mg

Quindi, 3.5 kg equivalgono a 3.500.000 mg.

Errori Comuni e Come Evitarli

Un errore comune è confondere i prefissi, specialmente quelli con suoni simili. Ad esempio, è facile confondere "milli" (m) con "mega" (M). Ricordare che "milli" indica una frazione (1/1000), mentre "mega" indica un multiplo (1.000.000). Un altro errore frequente è dimenticare la corretta potenza di 10 da utilizzare nella conversione. È sempre utile avere una tabella di riferimento a portata di mano quando si eseguono conversioni.

Inoltre, prestare attenzione alle unità di misura utilizzate nei calcoli. Assicurarsi che tutte le quantità siano espresse nella stessa unità prima di eseguire qualsiasi operazione matematica. Se si lavora con diverse unità, è necessario convertirle prima di procedere.

Applicazioni Pratiche Avanzate

Oltre agli esempi quotidiani, la tabella dei multipli e sottomultipli è fondamentale in campi più specialistici. Ad esempio:

• Nanotecnologie: In questo campo si lavora con dimensioni a livello nanometrico (miliardesimi di metro). Anche se non direttamente legati al grammo, la comprensione dei prefissi è cruciale.
• Astrofisica: Le masse delle stelle e dei pianeti sono espresse in unità enormi, spesso utilizzando potenze di 10 o unità derivate.
• Informatica: La capacità di memorizzazione dei computer è misurata in byte, kilobyte, megabyte, gigabyte, e così via. La comprensione dei multipli è essenziale per capire le dimensioni dei file e la capacità dei dispositivi di memorizzazione.

In questi contesti, la precisione e la corretta manipolazione delle unità di misura sono di primaria importanza.

Conclusioni

La tabella dei grammi multipli e sottomultipli, e la sua estensione a tutte le unità del Sistema Internazionale, è uno strumento indispensabile per chiunque lavori con misurazioni. La sua comprensione consente di semplificare la notazione, facilitare i calcoli e standardizzare le comunicazioni. Che si tratti di pesare ingredienti in cucina, calcolare dosi di farmaci, o analizzare dati scientifici, la conoscenza dei multipli e sottomultipli è una competenza fondamentale.

Invitiamo il lettore a esercitarsi con le conversioni, a consultare la tabella dei prefissi quando necessario, e a integrare questo concetto nella propria pratica quotidiana. La padronanza di questo strumento aprirà la porta a una comprensione più profonda del mondo che ci circonda e a una maggiore efficacia in una vasta gamma di attività.