Somma Degli Angoli Interni Di Un Pentagono

Capita spesso di trovarsi di fronte a figure geometriche complesse e sentirsi un po' sopraffatti. Specialmente quando si tratta di calcolare angoli e proprietà. Ma non temere! In questo articolo, affronteremo un caso specifico: la somma degli angoli interni di un pentagono. Lo faremo in modo chiaro, semplice e con un approccio che ti permetterà di capire *realmente* il perché di ogni passaggio. Perché alla fine, la geometria non è un insieme di formule da memorizzare, ma un modo per comprendere il mondo che ci circonda.

Perché Dovresti Preoccuparti della Somma degli Angoli Interni di un Pentagono?

Potresti chiederti: "Ma a cosa mi serve sapere la somma degli angoli interni di un pentagono nella vita di tutti i giorni?". In realtà, la geometria, anche quella apparentemente astratta, ha applicazioni concrete. Pensa all'architettura: la progettazione di edifici, ponti e strutture complesse richiede una profonda conoscenza delle forme geometriche e delle loro proprietà. I pentagoni, per esempio, compaiono in molte strutture, dai pavimenti decorati alle forme di alcuni edifici.

Inoltre, la comprensione dei principi geometrici sviluppa il pensiero logico e la capacità di risolvere problemi. Imparare a calcolare la somma degli angoli interni di un pentagono è un esercizio che allena la tua mente a ragionare in modo strutturato e a trovare soluzioni creative.

Infine, c'è la pura soddisfazione intellettuale di capire come funziona il mondo! La geometria è un linguaggio universale che ci permette di descrivere e interpretare la realtà.

Cominciamo dalle Basi: Cos'è un Pentagono?

Un pentagono è un poligono, ovvero una figura geometrica piana delimitata da una linea spezzata chiusa. In particolare, un pentagono è un poligono con cinque lati e, di conseguenza, cinque angoli. Esistono diverse tipologie di pentagono:

• Pentagono Regolare: Ha tutti i lati e tutti gli angoli uguali.
• Pentagono Irregolare: Ha lati e/o angoli di diversa misura.
• Pentagono Concavo: Ha almeno un angolo interno maggiore di 180 gradi.
• Pentagono Convesso: Tutti gli angoli interni sono minori di 180 gradi.

Indipendentemente dalla tipologia, la somma degli angoli interni di *qualsiasi* pentagono è sempre la stessa.

Il Metodo Triangolazione: La Chiave per la Soluzione

Il metodo più semplice per calcolare la somma degli angoli interni di un pentagono è quello della triangolazione. L'idea è di dividere il pentagono in triangoli, di cui conosciamo già la somma degli angoli interni (180 gradi). Ecco i passaggi:

1. Scegli un vertice del pentagono.
2. Traccia tutte le diagonali possibili da quel vertice. Una diagonale è un segmento che congiunge due vertici non consecutivi.
3. Osserva quanti triangoli hai ottenuto. In un pentagono, tracciando le diagonali da un vertice, otterrai sempre tre triangoli.

Ogni angolo del pentagono originale è stato "diviso" tra gli angoli dei triangoli che lo compongono. La somma degli angoli di questi tre triangoli è quindi uguale alla somma degli angoli interni del pentagono.

Il Calcolo Finale: La Formula Magica

Sappiamo che la somma degli angoli interni di un triangolo è 180 gradi. Dato che abbiamo diviso il pentagono in tre triangoli, la somma degli angoli interni del pentagono sarà:

3 triangoli * 180 gradi/triangolo = 540 gradi

Quindi, la somma degli angoli interni di qualsiasi pentagono è sempre 540 gradi. Questa è una regola generale che vale per tutti i pentagoni, indipendentemente dalla loro forma o dimensione.

Generalizzazione: La Formula per Qualsiasi Poligono

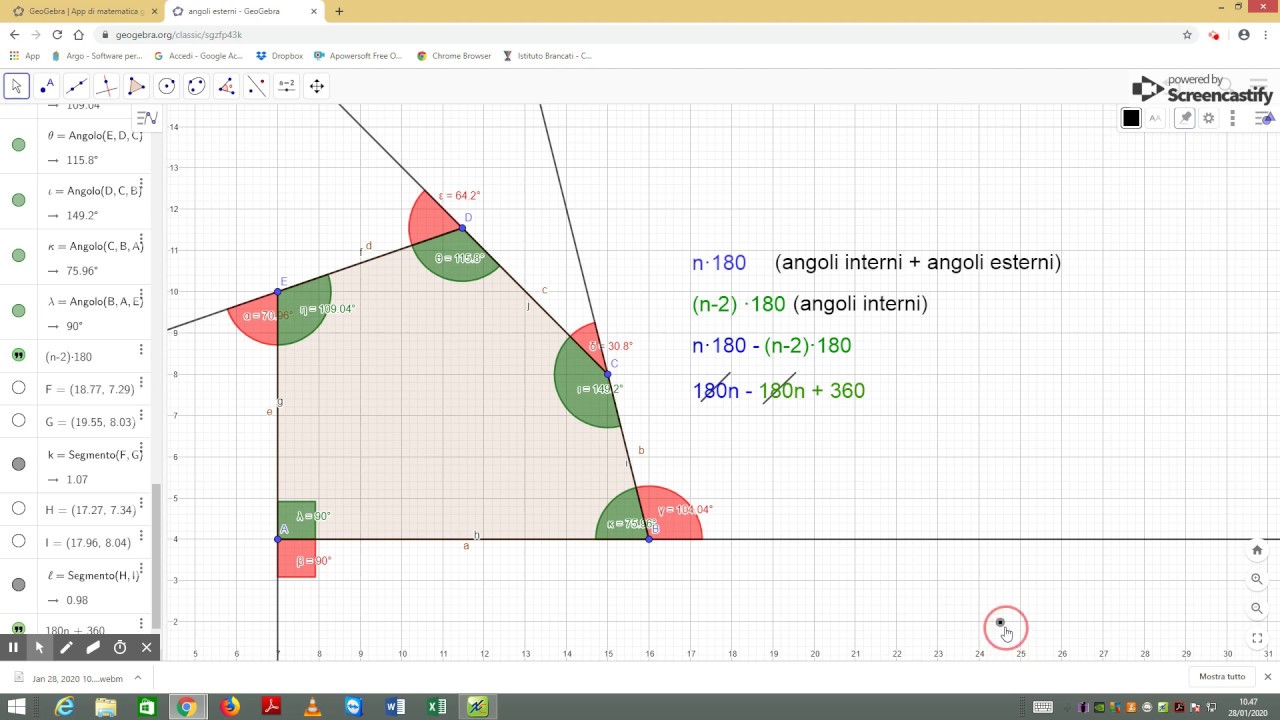
Il metodo della triangolazione può essere esteso a qualsiasi poligono. Esiste una formula generale per calcolare la somma degli angoli interni di un poligono con n lati:

Somma degli angoli interni = (n - 2) * 180 gradi

Nel caso del pentagono (n = 5):

Somma degli angoli interni = (5 - 2) * 180 gradi = 3 * 180 gradi = 540 gradi

Questa formula è una conseguenza diretta del metodo della triangolazione: da un vertice di un poligono con *n* lati, si possono tracciare (n - 3) diagonali, che dividono il poligono in (n - 2) triangoli.

Controargomentazioni: Perché Qualcuno Potrebbe Confondersi

A volte, si cade nell'errore di pensare che la somma degli angoli interni di un pentagono dipenda dalla sua forma. Questo è falso. La formula (n - 2) * 180 gradi dimostra che la somma degli angoli interni dipende solo dal numero di lati, non dalla loro lunghezza o dagli angoli individuali. Un pentagono irregolare avrà angoli diversi, ma la loro somma sarà sempre 540 gradi.

Un altro errore comune è confondere la somma degli angoli interni con la somma degli angoli esterni. La somma degli angoli esterni di qualsiasi poligono convesso è sempre 360 gradi, indipendentemente dal numero di lati.

Infine, è importante ricordare che questo metodo funziona per poligoni piani. La geometria sferica, ad esempio, ha regole diverse.

Applicazioni Pratiche e Risoluzione di Problemi

Ora che conosci la formula, proviamo ad applicarla in alcuni esempi pratici:

Esempio 1: Pentagono Regolare

In un pentagono regolare, tutti gli angoli sono uguali. Per trovare la misura di un singolo angolo, dividiamo la somma totale degli angoli interni per il numero di angoli:

Misura di un angolo = 540 gradi / 5 = 108 gradi

Quindi, ogni angolo di un pentagono regolare misura 108 gradi.

Esempio 2: Pentagono Irregolare con Angoli Noti

Supponiamo di avere un pentagono irregolare e di conoscere la misura di quattro dei suoi angoli: 90°, 100°, 120° e 110°. Qual è la misura del quinto angolo?

1. Somma gli angoli conosciuti: 90 + 100 + 120 + 110 = 420 gradi
2. Sottrai la somma degli angoli conosciuti dalla somma totale degli angoli interni di un pentagono: 540 - 420 = 120 gradi

Quindi, il quinto angolo misura 120 gradi.

Questi esempi dimostrano come la conoscenza della somma degli angoli interni di un pentagono può essere utile per risolvere problemi geometrici.

Consigli Utili per Ricordare la Formula

Ecco alcuni trucchi per memorizzare la formula e il concetto dietro la somma degli angoli interni di un pentagono:

• Visualizzazione: Immagina di dividere il pentagono in tre triangoli. Questo ti ricorderà che la somma degli angoli interni è 3 * 180 gradi.
• Associazione: Associa il numero 5 (lati del pentagono) al numero 3 (triangoli in cui si divide) e al numero 540 (somma degli angoli interni).
• Pratica: Risolvi diversi esercizi per mettere in pratica la formula e rafforzare la tua comprensione.
• Insegnare: Spiega il concetto a qualcun altro. Insegnare è un ottimo modo per consolidare la tua conoscenza.

Conclusioni: Un Passo Avanti nella Comprensione della Geometria

Congratulazioni! Ora sai come calcolare la somma degli angoli interni di un pentagono. Hai imparato il metodo della triangolazione, la formula generale per i poligoni e come applicare questa conoscenza per risolvere problemi pratici. Ricorda che la geometria non è solo un insieme di regole, ma un modo per comprendere il mondo che ci circonda. Continua a esplorare, a fare domande e a mettere in pratica ciò che hai imparato. La geometria è un viaggio affascinante che ti aprirà gli occhi su nuove prospettive.

Ora, pensa a un oggetto nella tua vita quotidiana che ha la forma di un pentagono. Riesci a immaginare come la conoscenza degli angoli interni potrebbe essere utile per progettarlo o analizzarlo?