Somma Degli Angoli Esterni Di Un Triangolo

Hai mai osservato attentamente un triangolo? Forse a scuola durante le lezioni di geometria, o magari mentre costruivi qualcosa. Tutti conosciamo i triangoli, ma oggi esploreremo un aspetto meno noto ma affascinante: la somma degli angoli esterni di un triangolo. Questo articolo è pensato per studenti delle scuole medie e superiori, appassionati di matematica e chiunque desideri rispolverare le proprie conoscenze geometriche. Preparati a scoprire un teorema sorprendente e a capire perché funziona!

Cos'è un Angolo Esterno?

Prima di addentrarci nel cuore della questione, definiamo cosa intendiamo per angolo esterno di un triangolo. Considera un triangolo qualsiasi. Prolunga uno dei suoi lati oltre il vertice. L'angolo formato da questo prolungamento e dal lato adiacente del triangolo è un angolo esterno. Ogni vertice di un triangolo ha, quindi, due angoli esterni, che sono congruenti (uguali) perché opposti al vertice.

Per chiarire, immaginiamo un triangolo ABC. Se prolunghiamo il lato AB oltre il punto B fino a un punto D, l'angolo CBD è un angolo esterno del triangolo ABC. Lo stesso procedimento può essere ripetuto per gli altri due lati, ottenendo così tre angoli esterni.

Ricorda: un angolo esterno e l'angolo interno adiacente (quello che condivide lo stesso vertice e lato) sono supplementari. Questo significa che la loro somma è sempre 180 gradi.

Il Teorema Fondamentale: La Somma degli Angoli Esterni

Ed ecco la parte più interessante: la somma degli angoli esterni di un triangolo, prendendo uno solo per ogni vertice, è sempre 360 gradi. Sembra quasi magico, vero? Ma c'è una spiegazione logica e rigorosa dietro a questo teorema.

Per dimostrarlo, utilizziamo alcune proprietà fondamentali dei triangoli e degli angoli:

La somma degli angoli interni di un triangolo è 180 gradi.
Un angolo esterno e l'angolo interno adiacente sono supplementari (sommano a 180 gradi).

Sia α, β, e γ gli angoli interni di un triangolo. Siano α', β', e γ' i rispettivi angoli esterni. Sappiamo che:

α + α' = 180°
β + β' = 180°
γ + γ' = 180°

Sommando queste tre equazioni, otteniamo:

(α + β + γ) + (α' + β' + γ') = 180° + 180° + 180° = 540°

Ma sappiamo anche che α + β + γ = 180° (somma degli angoli interni di un triangolo). Sostituendo, abbiamo:

180° + (α' + β' + γ') = 540°

Sottraendo 180° da entrambi i lati, otteniamo:

α' + β' + γ' = 360°

Quindi, abbiamo dimostrato che la somma degli angoli esterni di un triangolo è sempre 360 gradi!

Dimostrazione Alternativa e Intuitiva

Esiste un modo più intuitivo per capire questo teorema? Immagina di essere una formica che cammina lungo i lati del triangolo. Partendo da un vertice, cammini lungo un lato. Arrivato al vertice successivo, devi girare per seguire il lato successivo. L'angolo di cui devi girare è esattamente l'angolo esterno. Ripeti questo processo per tutti e tre i lati. Alla fine, avrai compiuto un giro completo intorno al triangolo, ritornando al punto di partenza e guardando nella stessa direzione di quando sei partito. Un giro completo corrisponde a 360 gradi. Pertanto, la somma degli angoli esterni (gli angoli di cui hai dovuto girare) deve essere 360 gradi.

Perché è Importante Questo Teorema?

Potresti chiederti: "Ok, ho capito, ma a cosa serve questo teorema?". La risposta è che ha diverse applicazioni pratiche e teoriche:

* Risoluzione di Problemi Geometrici: Conoscere questo teorema semplifica la risoluzione di molti problemi che coinvolgono angoli in figure geometriche complesse. * Architettura e Ingegneria: I principi geometrici, compreso questo teorema, sono fondamentali nella progettazione di edifici, ponti e altre strutture. * Grafica Computerizzata: La geometria è alla base della grafica computerizzata e della modellazione 3D. La comprensione degli angoli e delle loro relazioni è cruciale per creare immagini realistiche e accurate. * Sviluppo del Pensiero Logico: Studiare e dimostrare teoremi come questo aiuta a sviluppare il pensiero logico e la capacità di ragionamento deduttivo, competenze preziose in molti ambiti della vita.

Esempi Pratici

Vediamo alcuni esempi per capire meglio come applicare questo teorema:

* Esempio 1: In un triangolo, due angoli esterni misurano 120° e 100°. Quanto misura il terzo angolo esterno?

Soluzione: Sappiamo che la somma degli angoli esterni è 360°. Quindi, il terzo angolo esterno misura 360° - 120° - 100° = 140°.

* Esempio 2: Un angolo interno di un triangolo misura 60°. Qual è la misura del suo angolo esterno adiacente?

Soluzione: L'angolo esterno e l'angolo interno adiacente sono supplementari, quindi la loro somma è 180°. Pertanto, l'angolo esterno misura 180° - 60° = 120°.

* Esempio 3: In un triangolo rettangolo, un angolo acuto misura 30°. Quali sono le misure degli angoli esterni corrispondenti agli angoli acuti del triangolo?

Soluzione: Un angolo interno misura 30°, quindi il suo angolo esterno adiacente misura 180° - 30° = 150°. L'altro angolo acuto misura 60° (90°-30°), quindi il suo angolo esterno adiacente misura 180° - 60° = 120°. L'angolo retto (90°) ha un angolo esterno di 180°-90° = 90°.

Consigli per Ricordare il Teorema

Ecco alcuni suggerimenti per memorizzare e comprendere meglio il teorema della somma degli angoli esterni:

* Disegna: Disegna diversi triangoli e misura i loro angoli esterni. Verifica che la somma sia sempre 360°. * Spiega: Spiega il teorema a un amico o a un familiare. Insegnare è un ottimo modo per imparare! * Associa: Associa il teorema a un'immagine o a una metafora, come la formica che cammina intorno al triangolo. * Esercitati: Risolvi molti esercizi diversi per applicare il teorema in contesti diversi.

Oltre il Triangolo: Poligoni Generali

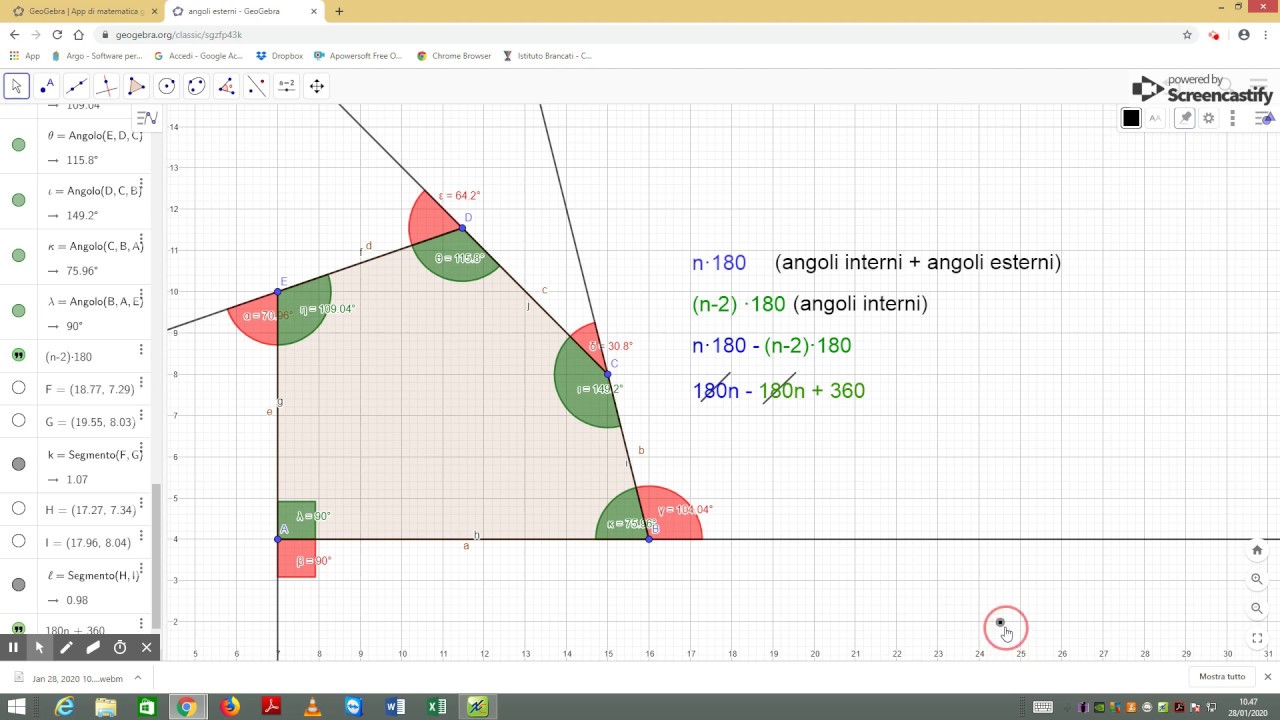
L'idea della somma degli angoli esterni può essere estesa anche a poligoni con più di tre lati. In generale, la somma degli angoli esterni di un poligono convesso (prendendo uno solo per ogni vertice) è sempre 360 gradi. Questo è un risultato notevole che dimostra l'eleganza e la coerenza della geometria.

Conclusione

Spero che questo viaggio alla scoperta della somma degli angoli esterni di un triangolo sia stato illuminante e interessante. Abbiamo visto non solo cos'è questo teorema, ma anche perché è vero e come può essere applicato. La prossima volta che vedrai un triangolo, ricordati di questo teorema e di come un semplice concetto geometrico possa rivelare una profonda bellezza matematica. Continua ad esplorare il mondo della matematica e scoprirai sempre nuove meraviglie! La matematica è ovunque, e comprenderla ci aiuta a comprendere meglio il mondo che ci circonda.