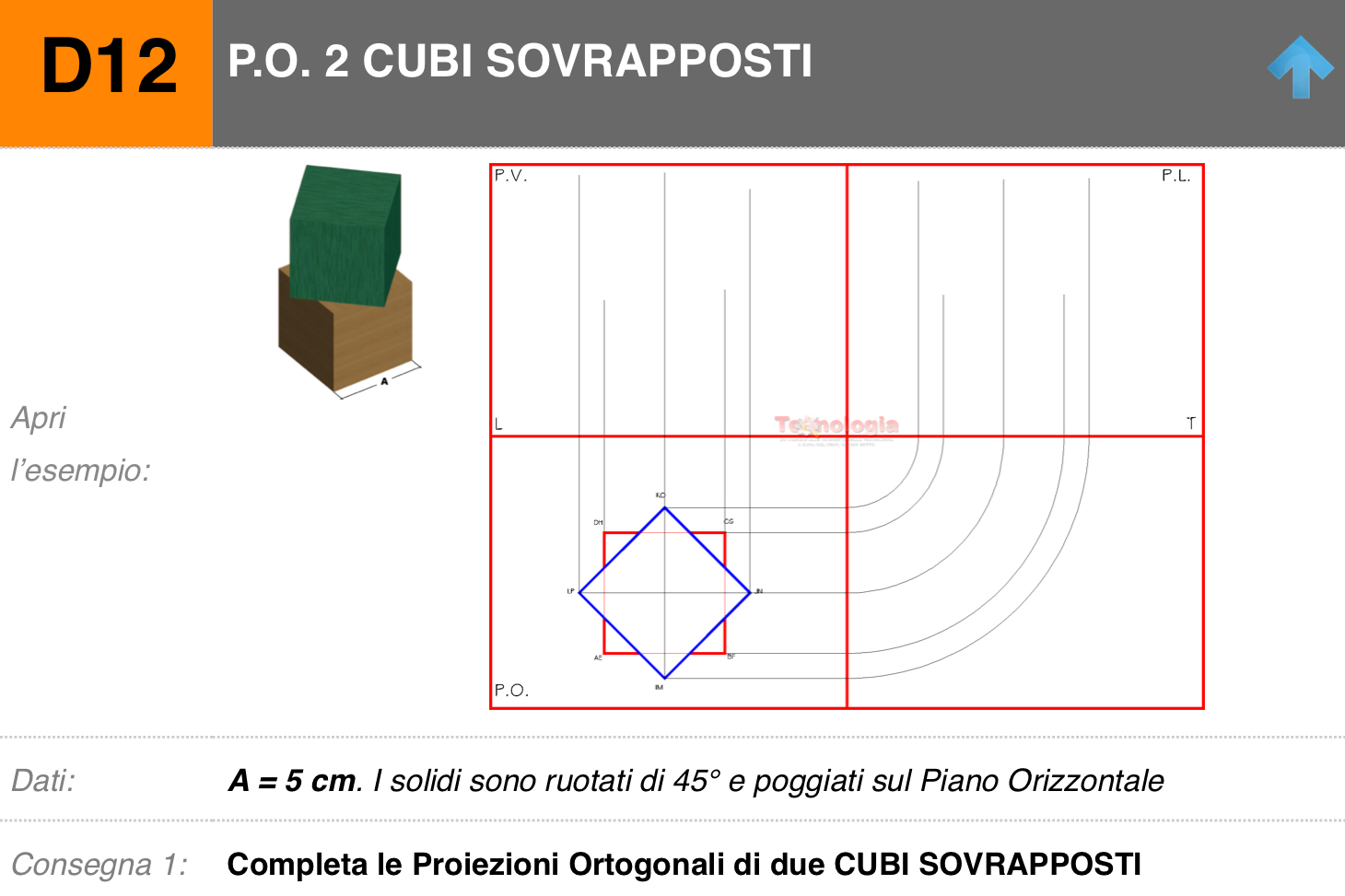
Solidi Sovrapposti Proiezioni Ortogonali Di Solidi

La rappresentazione di oggetti tridimensionali su una superficie bidimensionale è una sfida fondamentale in molti campi, dall'ingegneria all'architettura all'arte. Le proiezioni ortogonali rappresentano uno strumento potente e versatile per affrontare questa sfida. Quando parliamo di solidi sovrapposti e della loro proiezione ortogonale, la complessità aumenta notevolmente, richiedendo una comprensione approfondita dei principi geometrici e della loro applicazione pratica.
Principi Fondamentali delle Proiezioni Ortogonali
Le proiezioni ortogonali si basano sull'idea di proiettare un oggetto su uno o più piani di proiezione (tipicamente il piano orizzontale, il piano verticale e il piano laterale) utilizzando rette perpendicolari al piano stesso. Questo significa che ogni punto dell'oggetto viene proiettato sul piano lungo una retta che forma un angolo di 90 gradi con il piano. Il risultato è una serie di viste (piante, prospetti e sezioni) che, combinate, forniscono una descrizione completa della forma e delle dimensioni dell'oggetto.
I Piani di Proiezione
I tre piani di proiezione fondamentali sono:
- Piano Orizzontale (PO): Produce la pianta dell'oggetto.
- Piano Verticale (PV): Produce il prospetto frontale dell'oggetto.
- Piano Laterale (PL): Produce il prospetto laterale dell'oggetto.
Questi piani sono immaginati come ortogonali tra loro. Una volta eseguite le proiezioni, i piani vengono ribaltati per giacere sullo stesso piano, permettendo la visualizzazione simultanea delle tre viste. Questa disposizione standardizzata facilita la lettura e l'interpretazione dei disegni tecnici.
Il Concetto di Visibilità
Nelle proiezioni ortogonali, è cruciale considerare la visibilità delle linee e delle superfici. Le linee e le superfici visibili dall'osservatore vengono rappresentate con linee continue, mentre quelle nascoste vengono rappresentate con linee tratteggiate. Questa convenzione permette di distinguere chiaramente le parti dell'oggetto che sono direttamente esposte alla vista da quelle che sono ostruite.
Solidi Sovrapposti: La Complessità Aggiunta
Quando si tratta di solidi sovrapposti, la sfida principale consiste nel determinare quali parti di ciascun solido sono visibili e quali sono nascoste dagli altri solidi. La corretta rappresentazione richiede una comprensione approfondita della geometria dei solidi e delle loro relazioni spaziali.
Determinazione delle Intersezioni
Un aspetto fondamentale è la determinazione delle intersezioni tra i solidi. Queste intersezioni possono essere linee, curve o superfici complesse. Identificare e rappresentare accuratamente queste intersezioni è essenziale per una corretta interpretazione del disegno. L'uso di software CAD (Computer-Aided Design) può semplificare notevolmente questo processo, ma la comprensione dei principi geometrici sottostanti rimane fondamentale.
Gestione delle Priorità di Visibilità
Una volta determinate le intersezioni, è necessario stabilire le priorità di visibilità. Quale solido è davanti all'altro in una determinata zona? La risposta a questa domanda determina quali linee e superfici devono essere rappresentate come continue e quali come tratteggiate. Spesso, è necessario analizzare attentamente le viste proiettate da diverse angolazioni per determinare la corretta rappresentazione della visibilità.
Esempi di Solidi Sovrapposti
Consideriamo alcuni esempi concreti per illustrare le sfide nella rappresentazione di solidi sovrapposti:
- Un cilindro intersecato da un cubo: La linea di intersezione tra il cilindro e il cubo sarà una curva complessa che deve essere determinata con precisione. La visibilità delle parti del cilindro e del cubo dipenderà dalla loro posizione relativa.
- Due prismi rettangolari sovrapposti: In questo caso, le intersezioni saranno linee rette, ma la determinazione delle priorità di visibilità può essere comunque complessa, soprattutto se i prismi sono orientati in modo non allineato.
- Una sfera contenuta parzialmente dentro un cono: La proiezione ortogonale mostrerà un cerchio (la proiezione della sfera) e un triangolo (la proiezione del cono), ma la parte di cerchio nascosta dal triangolo dovrà essere rappresentata con linea tratteggiata.
Applicazioni Pratiche
Le proiezioni ortogonali di solidi sovrapposti trovano applicazione in una vasta gamma di settori. Alcuni esempi includono:
Ingegneria Meccanica
Nella progettazione di macchinari e componenti meccanici, le proiezioni ortogonali sono utilizzate per rappresentare assiemi complessi composti da numerosi solidi sovrapposti. La chiarezza e l'accuratezza della rappresentazione sono cruciali per garantire la corretta fabbricazione e il funzionamento del macchinario.
Architettura
Gli architetti utilizzano le proiezioni ortogonali per rappresentare edifici complessi, inclusi quelli con elementi strutturali sovrapposti o intersecanti. Le planimetrie, i prospetti e le sezioni sono tutti esempi di proiezioni ortogonali che forniscono una visione completa del progetto architettonico.
Design Industriale
Nel design industriale, le proiezioni ortogonali sono utilizzate per rappresentare prototipi e modelli di prodotti. La rappresentazione accurata delle forme e delle dimensioni è essenziale per la comunicazione tra designer, ingegneri e produttori.
Cartografia e GIS (Geographic Information Systems)
Anche se con delle differenze sostanziali, i principi delle proiezioni ortogonali sono alla base della cartografia. Le mappe, in fondo, sono proiezioni di elementi tridimensionali (il terreno, edifici, infrastrutture) su un piano bidimensionale. Nei sistemi GIS, la sovrapposizione di livelli informativi (strade, edifici, corsi d'acqua) può essere vista come una forma complessa di sovrapposizione di solidi, dove la corretta visualizzazione e interpretazione delle relazioni spaziali è fondamentale.
Strumenti e Tecniche Avanzate
Oltre ai metodi tradizionali di disegno a mano, sono disponibili numerosi software CAD che semplificano notevolmente la creazione e la manipolazione di proiezioni ortogonali di solidi sovrapposti. Questi software offrono funzionalità avanzate come:
- Modellazione 3D: Permettono di creare modelli tridimensionali accurati dei solidi, che possono poi essere proiettati automaticamente sui piani di proiezione.
- Rilevamento automatico delle intersezioni: Identificano automaticamente le intersezioni tra i solidi, risparmiando tempo e riducendo il rischio di errori.
- Gestione automatica della visibilità: Determinano automaticamente la visibilità delle linee e delle superfici, semplificando la creazione di disegni chiari e accurati.
- Rendering e visualizzazione: Permettono di creare immagini realistiche dei solidi, che possono essere utilizzate per la presentazione e la comunicazione del progetto.
L'uso di software CAD, combinato con una solida comprensione dei principi geometrici, permette di affrontare con successo anche i problemi più complessi di rappresentazione di solidi sovrapposti.
Conclusione
La proiezione ortogonale di solidi sovrapposti è una tecnica fondamentale in molti campi dell'ingegneria e del design. La comprensione dei principi di base, come i piani di proiezione, la visibilità e la determinazione delle intersezioni, è essenziale per creare rappresentazioni accurate e chiare. L'utilizzo di strumenti CAD moderni può notevolmente semplificare il processo, ma una solida base teorica rimane cruciale.
Ti invitiamo a esplorare ulteriormente questo argomento. Studia esempi pratici, sperimenta con software CAD e, soprattutto, non aver paura di porre domande. La padronanza delle proiezioni ortogonali è un investimento prezioso per qualsiasi professionista che lavori con la rappresentazione di oggetti tridimensionali.