Seno E Coseno Di Un Angolo

Ti sei mai chiesto come fanno i navigatori a orientarsi in mare aperto, o come gli architetti progettano edifici che sfidano la gravità? La risposta, in molti casi, si trova in due funzioni matematiche fondamentali: il seno e il coseno. Se la trigonometria ti spaventa un po', non preoccuparti! Questo articolo è pensato proprio per te, per rendere questi concetti accessibili e persino... *divertenti*.

Il Cerchio Trigonometrico: La Nostra Bussola

Immagina un cerchio perfetto, centrato sull'origine di un piano cartesiano. Questo è il nostro cerchio trigonometrico, il punto di partenza per capire seno e coseno. Il cerchio ha un raggio di lunghezza 1 (un'unità), il che semplifica enormemente i calcoli. Pensa a questo cerchio come a un orologio, ma invece di ore, abbiamo gradi (o radianti, ma per ora concentriamoci sui gradi).

Un Punto sul Cerchio e l'Angolo

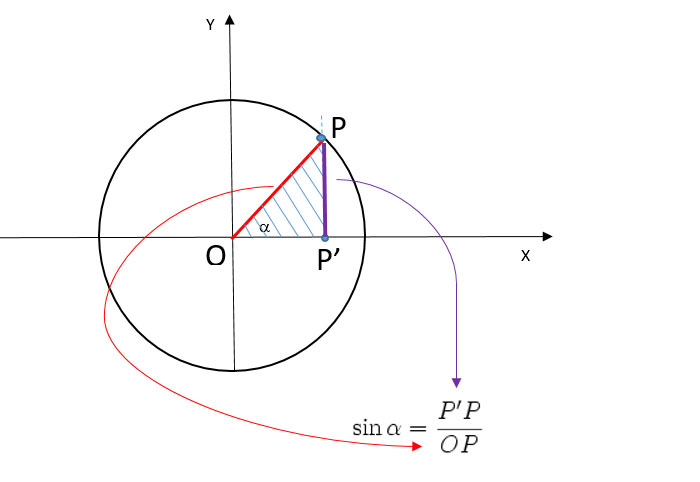
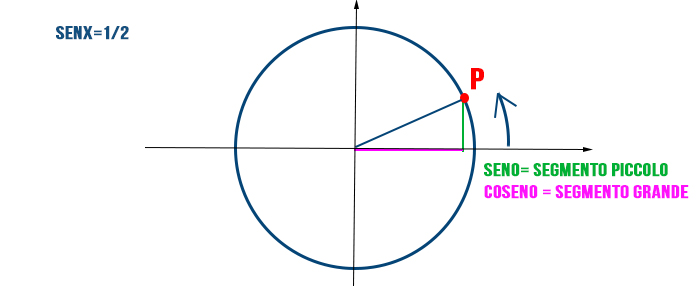
Ora, prendi un punto qualsiasi su questo cerchio. Collegalo all'origine con un segmento di retta. Questo segmento forma un angolo con l'asse x positivo. Chiameremo questo angolo "α" (alfa). La posizione di questo punto sul cerchio è completamente determinata dall'angolo α.

Il seno e il coseno sono semplicemente le coordinate di questo punto! Il coseno di α (scritto cos(α)) è l'ascissa (il valore sull'asse x) del punto. Il seno di α (scritto sin(α)) è l'ordinata (il valore sull'asse y) del punto.

Ricorda:

• cos(α) = ascissa del punto sul cerchio
• sin(α) = ordinata del punto sul cerchio

Facciamo un esempio. Se l'angolo α è 0°, il punto si trova sull'asse x positivo, alla coordinata (1, 0). Quindi, cos(0°) = 1 e sin(0°) = 0.

Esplorando gli Angoli Fondamentali

Vediamo cosa succede per alcuni angoli speciali:

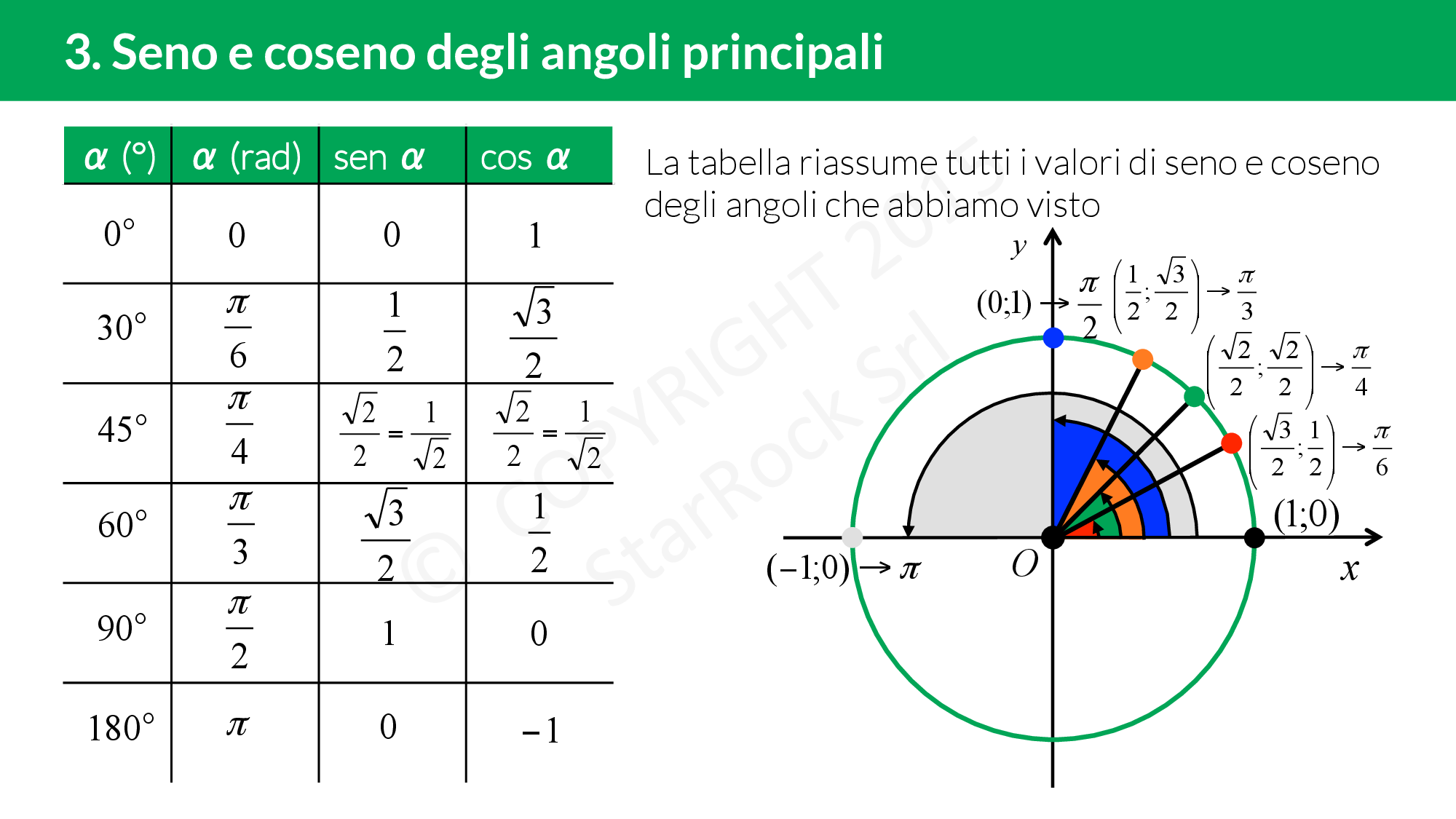
• α = 0°: cos(0°) = 1, sin(0°) = 0
• α = 90°: cos(90°) = 0, sin(90°) = 1
• α = 180°: cos(180°) = -1, sin(180°) = 0
• α = 270°: cos(270°) = 0, sin(270°) = -1
• α = 360°: cos(360°) = 1, sin(360°) = 0 (ritorniamo al punto di partenza!)

Nota come il seno e il coseno oscillano tra -1 e 1. Questo perché il punto sul cerchio trigonometrico non può mai andare oltre queste coordinate.

Il Quadrante e i Segni di Seno e Coseno

Il piano cartesiano è diviso in quattro quadranti. Il segno del seno e del coseno dipende dal quadrante in cui si trova l'angolo:

• I Quadrante (0° < α < 90°): cos(α) > 0, sin(α) > 0 (entrambi positivi)
• II Quadrante (90° < α < 180°): cos(α) < 0, sin(α) > 0 (coseno negativo, seno positivo)
• III Quadrante (180° < α < 270°): cos(α) < 0, sin(α) < 0 (entrambi negativi)
• IV Quadrante (270° < α < 360°): cos(α) > 0, sin(α) < 0 (coseno positivo, seno negativo)

Puoi memorizzare questo con una frase: "All Students Take Calculus". Le iniziali di ogni parola indicano quali funzioni sono positive in quel quadrante (All nel I quadrante, Sine nel II, Tangent nel III e Cosine nel IV). (Nota: la tangente è il rapporto tra seno e coseno, che vedremo dopo.)

Angoli Notevoli e i Loro Valori

Alcuni angoli compaiono frequentemente nei problemi di trigonometria. È utile conoscere i loro valori di seno e coseno a memoria:

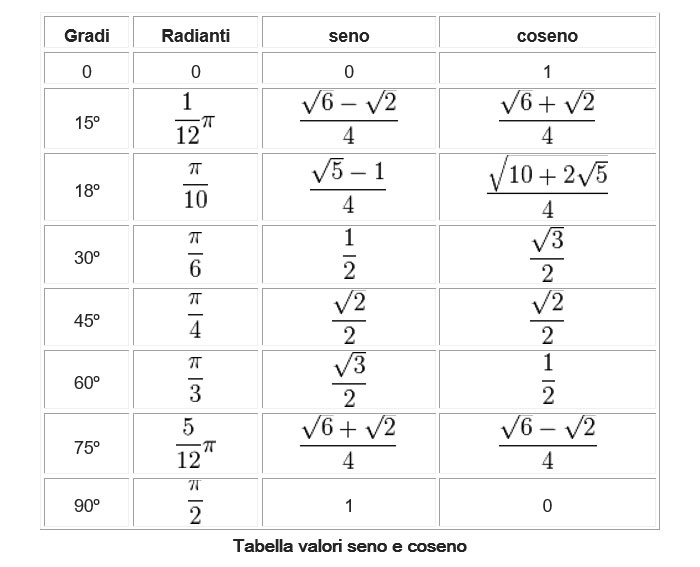
• 30° (π/6 radianti): cos(30°) = √3/2, sin(30°) = 1/2
• 45° (π/4 radianti): cos(45°) = √2/2, sin(45°) = √2/2
• 60° (π/3 radianti): cos(60°) = 1/2, sin(60°) = √3/2

Questi valori derivano da triangoli rettangoli speciali (30-60-90 e 45-45-90). Impararli ti farà risparmiare tempo prezioso durante gli esami!

Applicazioni Pratiche: Oltre l'Aula di Matematica

Il seno e il coseno non sono solo concetti astratti. Hanno applicazioni reali e concrete in molti campi:

• Navigazione: Come accennato all'inizio, i navigatori utilizzano seno e coseno per calcolare rotte e distanze, basandosi sulla posizione delle stelle e del sole.
• Ingegneria: Gli ingegneri usano seno e coseno per analizzare forze, movimenti oscillatori (come le vibrazioni di un ponte) e onde sonore.
• Fisica: La fisica è piena di esempi: dal moto dei proiettili all'analisi dei circuiti elettrici.
• Architettura: Gli architetti li utilizzano per progettare strutture stabili e calcolare angoli e lunghezze.
• Grafica computerizzata: Il seno e il coseno sono essenziali per creare animazioni, rotazioni e proiezioni 3D.

Per esempio, immagina di voler calcolare l'altezza di un edificio. Se conosci la distanza da cui stai osservando l'edificio e l'angolo di elevazione della cima dell'edificio, puoi usare la tangente dell'angolo (che è sin(α)/cos(α)) per calcolare l'altezza.

Seno, Coseno e Triangoli Rettangoli

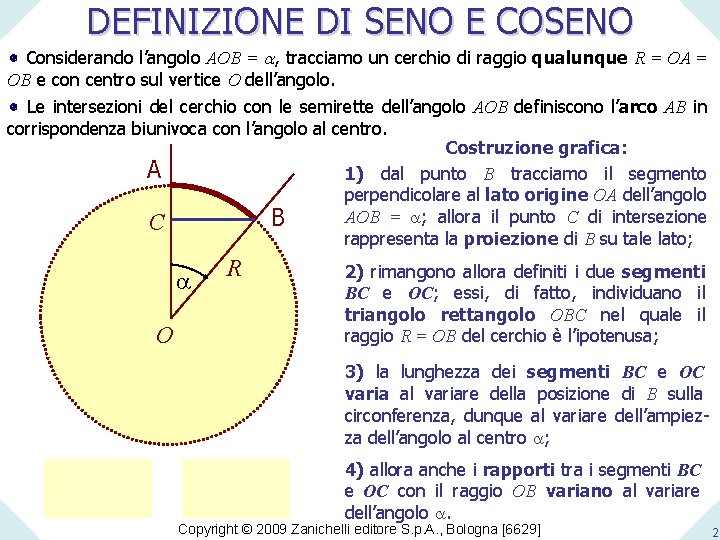
La relazione tra seno e coseno diventa particolarmente chiara nei triangoli rettangoli.

Considera un triangolo rettangolo con un angolo acuto α. Il lato opposto all'angolo α è chiamato "opposto", il lato adiacente all'angolo α (che non è l'ipotenusa) è chiamato "adiacente", e il lato più lungo è l'ipotenusa.

Allora:

• sin(α) = opposto / ipotenusa
• cos(α) = adiacente / ipotenusa

Questa è un'altra definizione di seno e coseno, equivalente a quella basata sul cerchio trigonometrico. Infatti, se disegni un triangolo rettangolo all'interno del cerchio trigonometrico, con l'ipotenusa pari al raggio del cerchio (che è 1), ottieni che l'opposto è proprio l'ordinata del punto e l'adiacente è l'ascissa.

Riflessioni e Simmetrie: Proprietà Importanti

Il seno e il coseno hanno interessanti proprietà di simmetria. Queste proprietà derivano direttamente dalla simmetria del cerchio trigonometrico:

• sin(-α) = -sin(α) (Il seno è una funzione dispari)
• cos(-α) = cos(α) (Il coseno è una funzione pari)
• sin(90° - α) = cos(α)
• cos(90° - α) = sin(α)

Queste proprietà ti permettono di semplificare espressioni trigonometriche e risolvere equazioni.

Funzioni Periodiche: Un Comportamento Ondulatorio

Sia il seno che il coseno sono funzioni periodiche con periodo 360° (o 2π radianti). Ciò significa che il loro valore si ripete ogni 360 gradi.

In altre parole:

• sin(α + 360°) = sin(α)
• cos(α + 360°) = cos(α)

Questa periodicità è fondamentale per descrivere fenomeni oscillatori, come le onde sonore, le onde luminose e il moto armonico semplice.

Oltre il Seno e il Coseno: Le Altre Funzioni Trigonometriche

Oltre al seno e al coseno, ci sono altre funzioni trigonometriche, tra cui:

• Tangente (tan(α)): tan(α) = sin(α) / cos(α)
• Cotangente (cot(α)): cot(α) = cos(α) / sin(α) = 1 / tan(α)
• Secante (sec(α)): sec(α) = 1 / cos(α)
• Cosecante (csc(α)): csc(α) = 1 / sin(α)

Queste funzioni derivano dal seno e dal coseno e sono utili per risolvere problemi trigonometrici più complessi.

Consigli Pratici per Imparare Seno e Coseno

Ecco alcuni suggerimenti per padroneggiare seno e coseno:

• Visualizza il cerchio trigonometrico: Immagina sempre il cerchio trigonometrico quando pensi al seno e al coseno.
• Memorizza i valori degli angoli notevoli: Imparare a memoria i valori di seno e coseno per 30°, 45° e 60° ti farà risparmiare tempo.
• Fai pratica con gli esercizi: Risolvi molti esercizi diversi per applicare le tue conoscenze.
• Usa risorse online: Ci sono molte risorse online, come video, tutorial e calcolatori, che possono aiutarti a capire meglio il seno e il coseno.
• Non avere paura di chiedere aiuto: Se hai difficoltà, chiedi aiuto al tuo insegnante, a un compagno di classe o a un tutor.

Conclusione: Un Mondo di Possibilità Trigonometriche

Il seno e il coseno sono strumenti potenti che aprono le porte a un mondo di possibilità matematiche e scientifiche. Con un po' di pratica e comprensione, potrai padroneggiare questi concetti e applicarli a una vasta gamma di problemi. Ricorda, la trigonometria non è solo un insieme di formule, ma un modo per capire e modellare il mondo che ci circonda!

Quindi, la prossima volta che vedi un edificio imponente, un'onda che si infrange sulla spiaggia o senti la musica che ti fa vibrare, pensa al seno e al coseno: sono lì, dietro le quinte, a rendere tutto possibile.