Se Una Funzione è Derivabile Allora è Continua

Capita spesso, studiando matematica, di imbattersi in affermazioni che sembrano semplici ma che nascondono insidie. Una di queste è la relazione tra derivabilità e continuità di una funzione. Se una funzione è derivabile in un punto, allora è anche continua in quel punto. Ma cosa significa davvero e perché è importante? Cerchiamo di esplorare questo concetto insieme, rendendolo accessibile e comprensibile a tutti.

Molti studenti, e anche professionisti che non usano la matematica quotidianamente, si chiedono perché dovrebbero preoccuparsi di questa relazione. La risposta è che questa connessione è fondamentale per capire come le funzioni si comportano, e quindi come possiamo modellare il mondo reale con precisione. Pensate alla fisica, all'ingegneria, all'economia: tutti questi campi usano funzioni per descrivere fenomeni. Sapere quando una funzione è "liscia" (derivabile) ci permette di fare previsioni e prendere decisioni più informate.

Continuità e Derivabilità: Le Definizioni Chiave

Prima di addentrarci nella dimostrazione e nelle implicazioni, ripassiamo brevemente le definizioni di continuità e derivabilità.

Cos'è la Continuità?

Intuitivamente, una funzione è continua in un punto se si può disegnare il suo grafico senza alzare la penna dal foglio in quel punto. Più formalmente, una funzione f(x) è continua in un punto x₀ se:

Esiste il limite di f(x) per x che tende a x₀.
f(x₀) è definito.
Il limite di f(x) per x che tende a x₀ è uguale a f(x₀).

In termini ancora più semplici: avvicinandoci a x₀, il valore della funzione si avvicina al valore della funzione in x₀.

Cos'è la Derivabilità?

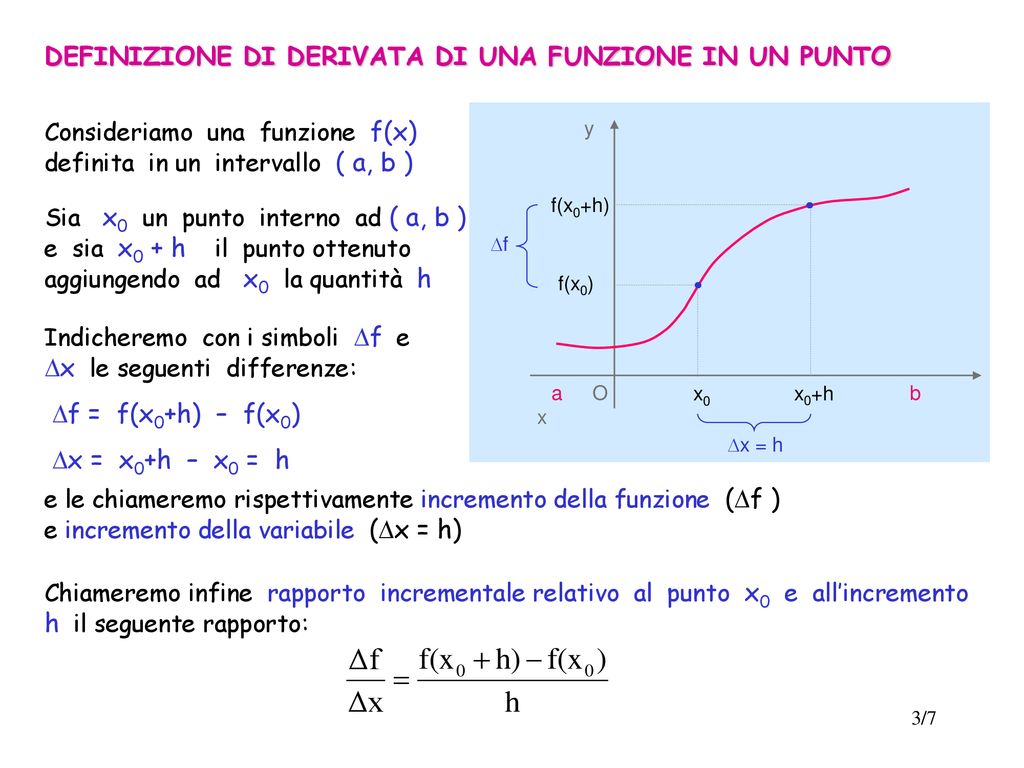
La derivata di una funzione in un punto rappresenta la pendenza della retta tangente al grafico della funzione in quel punto. Formalmente, una funzione f(x) è derivabile in un punto x₀ se esiste il limite:

f'(x₀) = lim_h→0 (f(x₀ + h) - f(x₀)) / h

Questo limite rappresenta il rapporto incrementale, e se questo limite esiste e è finito, allora la funzione è derivabile in x₀.

Il Teorema Fondamentale: Derivabilità Implica Continuità

Ora che abbiamo le definizioni chiare, possiamo enunciare il teorema chiave: se una funzione f(x) è derivabile in un punto x₀, allora è anche continua in x₀.

Dimostrazione:

Vogliamo dimostrare che lim_x→x₀ f(x) = f(x₀). Possiamo riscrivere f(x) come:

f(x) = f(x) - f(x₀) + f(x₀)

Quindi, calcoliamo il limite per x che tende a x₀:

lim_x→x₀ f(x) = lim_x→x₀ [f(x) - f(x₀) + f(x₀)]

lim_x→x₀ f(x) = lim_x→x₀ [f(x) - f(x₀)] + lim_x→x₀ f(x₀)

lim_x→x₀ f(x) = lim_x→x₀ [f(x) - f(x₀)] + f(x₀)

Ora, moltiplichiamo e dividiamo il primo termine per (x - x₀):

lim_x→x₀ f(x) = lim_x→x₀ [(f(x) - f(x₀)) / (x - x₀) * (x - x₀)] + f(x₀)

Poiché f(x) è derivabile in x₀, sappiamo che lim_x→x₀ (f(x) - f(x₀)) / (x - x₀) = f'(x₀). Inoltre, lim_x→x₀ (x - x₀) = 0. Quindi:

lim_x→x₀ f(x) = f'(x₀) * 0 + f(x₀)

lim_x→x₀ f(x) = f(x₀)

Questo dimostra che se f(x) è derivabile in x₀, allora è anche continua in x₀.

Il Viceversa Non è Vero: Continuità Non Implica Derivabilità

È fondamentale sottolineare che il contrario non è vero! Una funzione può essere continua in un punto senza essere derivabile in quel punto. Questo è un concetto che spesso crea confusione. Pensate a una funzione che ha un "angolo" acuto in un certo punto, come la funzione valore assoluto f(x) = |x| nel punto x = 0. La funzione è continua in x = 0, ma non è derivabile perché la pendenza cambia bruscamente.

Altri esempi includono funzioni con:

Punti angolosi: Come già detto, f(x) = |x|.
Cuspidi: Punti in cui la derivata tende all'infinito da entrambi i lati.
Tangenti verticali: Punti in cui la retta tangente è verticale.

Questi esempi ci ricordano che la continuità è una condizione necessaria, ma non sufficiente per la derivabilità.

Implicazioni Pratiche e Real-World

Ma perché tutto questo è importante al di là della teoria matematica? Ecco alcuni esempi:

Fisica: Immaginate di modellare la posizione di un oggetto in movimento. Se la posizione è descritta da una funzione non derivabile, significa che l'oggetto subisce un cambio di velocità istantaneo (una discontinuità nella velocità), cosa che non è fisicamente realistica.
Ingegneria: Nella progettazione di ponti o edifici, è cruciale assicurarsi che le funzioni che descrivono le sollecitazioni siano derivabili, perché una discontinuità potrebbe indicare un punto debole nella struttura.
Economia: Nei modelli economici, la derivabilità delle funzioni di domanda e offerta permette di calcolare elasticità e ottimizzare le strategie di mercato.

In sintesi, la derivabilità assicura una certa "regolarità" e "prevedibilità" nel comportamento delle funzioni, che è essenziale per modellare e comprendere il mondo che ci circonda.

Contraddizioni e Approfondimenti

Alcuni potrebbero obiettare che esistono modelli che usano funzioni non derivabili per descrivere la realtà. Ad esempio, la teoria del caos spesso coinvolge sistemi dinamici con sensibilità alle condizioni iniziali, che possono portare a comportamenti apparentemente discontinui. È vero, ma anche in questi casi, si cerca di approssimare tali sistemi con funzioni derivabili su intervalli più piccoli, per poter applicare gli strumenti dell'analisi matematica. L'uso di funzioni non derivabili è spesso una semplificazione o un'approssimazione, non la descrizione ultima della realtà.

Un'altra questione interessante è l'esistenza di funzioni continue ovunque ma non derivabili in nessun punto (funzioni di Weierstrass). Queste funzioni sono un esempio affascinante di come l'intuizione geometrica può ingannare, e mostrano che la continuità, da sola, non dice molto sulla "regolarità" di una funzione.

Risolvere i Dubbi e Andare Avanti

Spero che questa discussione abbia chiarito la relazione tra derivabilità e continuità. Ricordate, derivabilità implica continuità, ma il contrario non è vero. Tenete a mente gli esempi con i punti angolosi e le cuspidi. Visualizzate i grafici delle funzioni e cercate di capire intuitivamente perché la derivata non esiste in quei punti.

Se avete ancora dubbi, provate a fare questi esercizi: