Raggio Per Raggio Per 3 14
Il concetto di "Raggio Per Raggio Per 3,14", espresso matematicamente come r * r * π, è una formula fondamentale che descrive l'area di un cerchio. Questo apparentemente semplice calcolo ha implicazioni profonde e pervasive, influenzando una vasta gamma di discipline scientifiche, ingegneristiche e artistiche. Comprendere appieno questa formula e le sue applicazioni è essenziale per chiunque si avvicini a campi che richiedono un'analisi geometrica o una modellazione spaziale.
L'Essenza della Formula: Area di un Cerchio
L'area di un cerchio rappresenta la quantità di spazio bidimensionale contenuto all'interno della sua circonferenza. La formula r * r * π (o πr2) offre un metodo preciso per calcolare questa area, basato su un'unica misura: il raggio.
Il Raggio: la Chiave del Cerchio
Il raggio (r) di un cerchio è la distanza dal centro del cerchio a qualsiasi punto sulla sua circonferenza. È un parametro fondamentale perché definisce completamente le dimensioni del cerchio. Conoscendo il raggio, possiamo determinare non solo l'area, ma anche la circonferenza (2πr) e il diametro (2r).
Pi Greco (π): una Costante Universale
Pi Greco (π), approssimativamente uguale a 3,14159, è una costante matematica che rappresenta il rapporto tra la circonferenza di un cerchio e il suo diametro. È un numero irrazionale e trascendente, il che significa che non può essere espresso come una frazione semplice e le sue cifre decimali si estendono all'infinito senza ripetizioni. La sua presenza nella formula dell'area del cerchio sottolinea l'intrinseca relazione tra la geometria del cerchio e questa costante fondamentale.
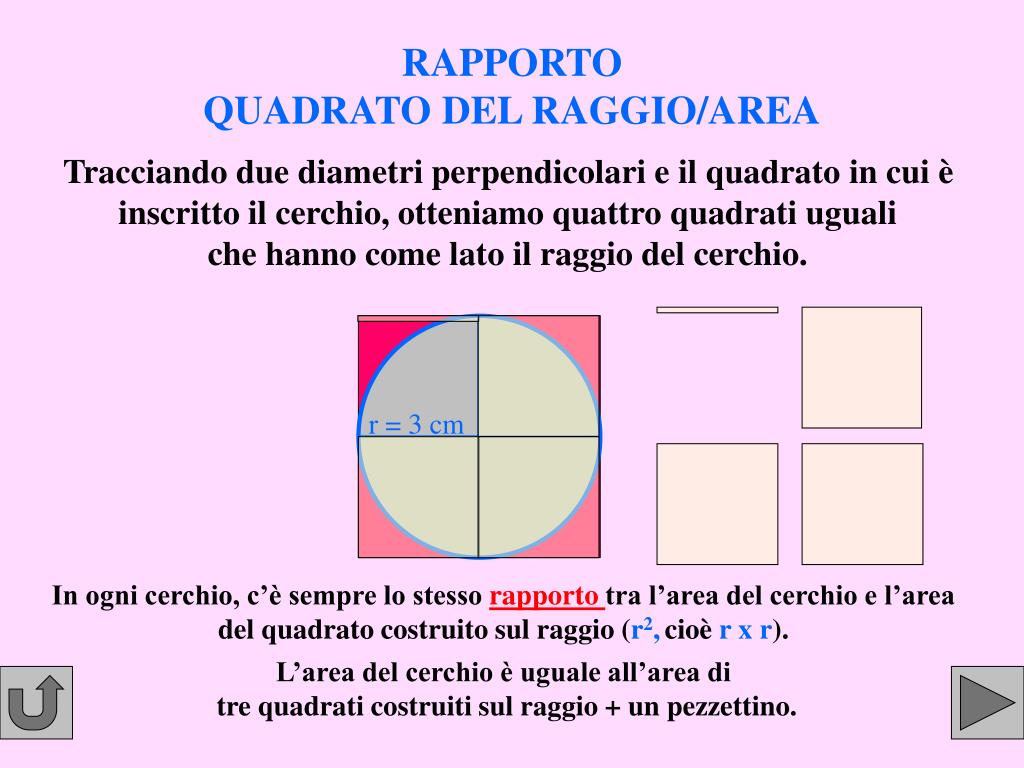
La Derivazione: Un Approccio Concettuale
Sebbene la formula sia ampiamente accettata, è utile comprendere da dove proviene. Un modo per visualizzarla è immaginare di dividere il cerchio in un numero sempre crescente di spicchi, come fette di torta. Se questi spicchi vengono poi riarrangiati per formare una figura simile a un parallelogramma, la sua altezza si avvicina al raggio del cerchio e la sua base si avvicina alla metà della circonferenza (πr). L'area di questo "parallelogramma" è quindi r * πr, che è uguale a πr2.
Applicazioni Pratiche e Real-World
La formula r * r * π non è solo un esercizio teorico; trova applicazioni concrete in una vasta gamma di settori.
Ingegneria e Architettura
Nel campo dell'ingegneria, il calcolo dell'area di un cerchio è cruciale per progettare tubi, condotti e serbatoi cilindrici. Ad esempio, determinare la capacità di un serbatoio circolare o la portata di un tubo richiede la conoscenza dell'area della sua sezione trasversale. In architettura, la formula viene utilizzata per calcolare la superficie di cupole, archi e altre strutture circolari, influenzando la quantità di materiali necessari e la stabilità strutturale. Considerate la costruzione del Pantheon a Roma, la cui cupola emisferica richiede calcoli precisi dell'area per garantire la sua integrità.
Scienza e Matematica
In fisica, la formula è essenziale per calcolare l'area di sezioni trasversali in esperimenti di dispersione di particelle o per determinare la densità di flusso di energia attraverso una superficie circolare. In astronomia, viene utilizzata per calcolare l'area di dischi di accrescimento attorno ai buchi neri o per stimare la dimensione apparente dei pianeti e delle stelle. L'area di un telescopio, calcolata con questa formula, determina la sua capacità di raccogliere la luce.
Produzione e Design
Nella produzione, la formula è utilizzata per calcolare la quantità di materiale necessario per tagliare forme circolari da lamine di metallo, tessuti o altri materiali. Nel design, l'area di cerchi influenza l'estetica e la funzionalità di oggetti che vanno dai pulsanti ai quadranti degli orologi. Pensate alla produzione di CD e DVD: la precisione nel calcolo dell'area è cruciale per garantire la corretta funzionalità del disco.
Statistica e Probabilità
Anche se meno ovvio, il concetto di area del cerchio gioca un ruolo in alcune applicazioni di statistica e probabilità. Ad esempio, la distribuzione normale bidimensionale (spesso visualizzata come una "collina" centrata) ha contorni circolari di uguale densità di probabilità. Il calcolo della probabilità che un punto casuale cada all'interno di un determinato raggio dal centro richiede la comprensione dell'area del cerchio.
Esempi Quantificabili
- Piscina Circolare: Immaginate una piscina circolare con un raggio di 5 metri. L'area della piscina sarebbe π * 52 = 78,54 metri quadrati (approssimativamente). Questo calcolo è fondamentale per determinare la quantità di acqua necessaria per riempire la piscina.
- Pizza: Una pizza con un diametro di 30 cm (raggio di 15 cm) ha un'area di π * 152 = 706,86 cm quadrati (approssimativamente). Questo influenza il prezzo che si è disposti a pagare per la pizza e il confronto tra offerte diverse.
- Cavo Elettrico: Un cavo elettrico con un raggio di 2 mm ha un'area di sezione trasversale di π * 22 = 12,57 mm quadrati (approssimativamente). Quest'area è cruciale per determinare la capacità di carico di corrente del cavo.
Oltre la Formula: Riflessioni sul Cerchio
Il cerchio, e di conseguenza la sua area, è una figura geometrica ricca di significato simbolico. Rappresenta la completezza, l'infinito e l'unità. La sua onnipresenza nella natura, dalle orbite planetarie alle bolle di sapone, testimonia la sua intrinseca importanza. La formula πr2 è quindi molto più di una semplice equazione; è una finestra sulla natura fondamentale della geometria e del mondo che ci circonda.
Conclusione e Call to Action
La formula "Raggio Per Raggio Per 3,14" (πr2) è un potente strumento per comprendere e quantificare il mondo che ci circonda. Dalla progettazione di edifici alla modellazione di fenomeni fisici, l'area del cerchio gioca un ruolo cruciale. Incoraggiamo tutti a esplorare ulteriormente le applicazioni di questa formula nei propri campi di interesse e a sviluppare un apprezzamento più profondo per la bellezza e l'utilità della geometria.
Comprendere i principi fondamentali di questa formula è essenziale per una solida base in matematica e scienze. Esercitatevi a calcolare l'area di diversi cerchi con raggi diversi per consolidare la vostra comprensione. Sperimentate con strumenti di calcolo online e software di geometria per visualizzare l'area del cerchio in azione.
Che siate studenti, ingegneri, artisti o semplicemente curiosi del mondo che vi circonda, la formula "Raggio Per Raggio Per 3,14" è una chiave per sbloccare una comprensione più profonda della realtà geometrica.