Radice Quadrata Approssimata Per Difetto A Meno Di 0 1

Hai mai avuto bisogno di calcolare rapidamente la radice quadrata di un numero, magari senza una calcolatrice a portata di mano? Questo articolo ti guiderà attraverso un metodo semplice e pratico per trovare un'approssimazione per difetto della radice quadrata, con un'accuratezza di 0.1. Questo metodo è utile in molte situazioni quotidiane, dalla cucina alla falegnameria, e ti aiuterà a sviluppare un intuito più forte per i numeri. Questo articolo è pensato per studenti delle scuole medie e superiori, appassionati di matematica e chiunque voglia migliorare le proprie capacità di calcolo mentale.

Cosa significa "Radice Quadrata Approssimata Per Difetto"?

Prima di addentrarci nel metodo, chiariamo alcuni concetti fondamentali:

Radice Quadrata: La radice quadrata di un numero (ad esempio, √25) è quel numero che, moltiplicato per se stesso, dà il numero originale. In questo caso, √25 = 5 perché 5 * 5 = 25.
Approssimazione: Un'approssimazione è un valore vicino a quello vero, ma non necessariamente identico. Ad esempio, 3.14 è un'approssimazione di π (pi greco).
Per Difetto: "Per difetto" significa che l'approssimazione è *inferiore* al valore reale. Ad esempio, se la radice quadrata di un numero è 6.7, un'approssimazione per difetto potrebbe essere 6.6.
A meno di 0.1: Questo significa che la differenza tra la nostra approssimazione e la vera radice quadrata deve essere inferiore a 0.1. In altre parole, dobbiamo essere precisi al decimo.

In sintesi, vogliamo trovare un numero che sia leggermente più piccolo della vera radice quadrata del numero che stiamo considerando, e che sia preciso entro un decimo di unità.

Il Metodo Passo-Passo

Ecco un metodo pratico per calcolare la radice quadrata approssimata per difetto a meno di 0.1:

Passo 1: Trova il quadrato perfetto più vicino (inferiore)

Individua il quadrato perfetto più grande che sia inferiore al numero di cui vuoi calcolare la radice quadrata. Un quadrato perfetto è un numero che si ottiene elevando al quadrato un numero intero (es: 1, 4, 9, 16, 25, 36...).

Esempio: Vogliamo trovare la radice quadrata approssimata di 27. I quadrati perfetti inferiori a 27 sono: 1, 4, 9, 16, 25. Il più grande tra questi è 25.

Passo 2: Calcola la radice quadrata del quadrato perfetto

Calcola la radice quadrata del quadrato perfetto che hai trovato al passo precedente. Questa sarà la parte intera della nostra approssimazione.

Esempio: La radice quadrata di 25 è 5. Quindi, la parte intera della nostra approssimazione sarà 5.

Passo 3: Stima la parte decimale

Questo è il passo più cruciale. Dobbiamo stimare la parte decimale, assicurandoci che l'approssimazione sia *per difetto* e con un'accuratezza di 0.1. Possiamo farlo provando diversi decimali e verificando se il quadrato del numero risultante è inferiore al numero originale.

Esempio: Sappiamo che la radice quadrata di 27 è tra 5 e 6. Proviamo con 5.1: 5.1 * 5.1 = 26.01. Questo è inferiore a 27.

Proviamo con 5.2: 5.2 * 5.2 = 27.04. Questo è *superiore* a 27.

Quindi, 5.1 è una buona approssimazione per difetto a meno di 0.1.

Passo 4: Verifica l'accuratezza

Assicurati che la differenza tra la tua approssimazione e la vera radice quadrata sia inferiore a 0.1. Se hai una calcolatrice, puoi confrontare il tuo risultato con il valore reale.

Esempio: La radice quadrata di 27 (con una calcolatrice) è circa 5.196. La differenza tra 5.1 e 5.196 è circa 0.096, che è inferiore a 0.1. Quindi, la nostra approssimazione è accurata.

Esempi Pratici

Vediamo altri esempi per consolidare il metodo:

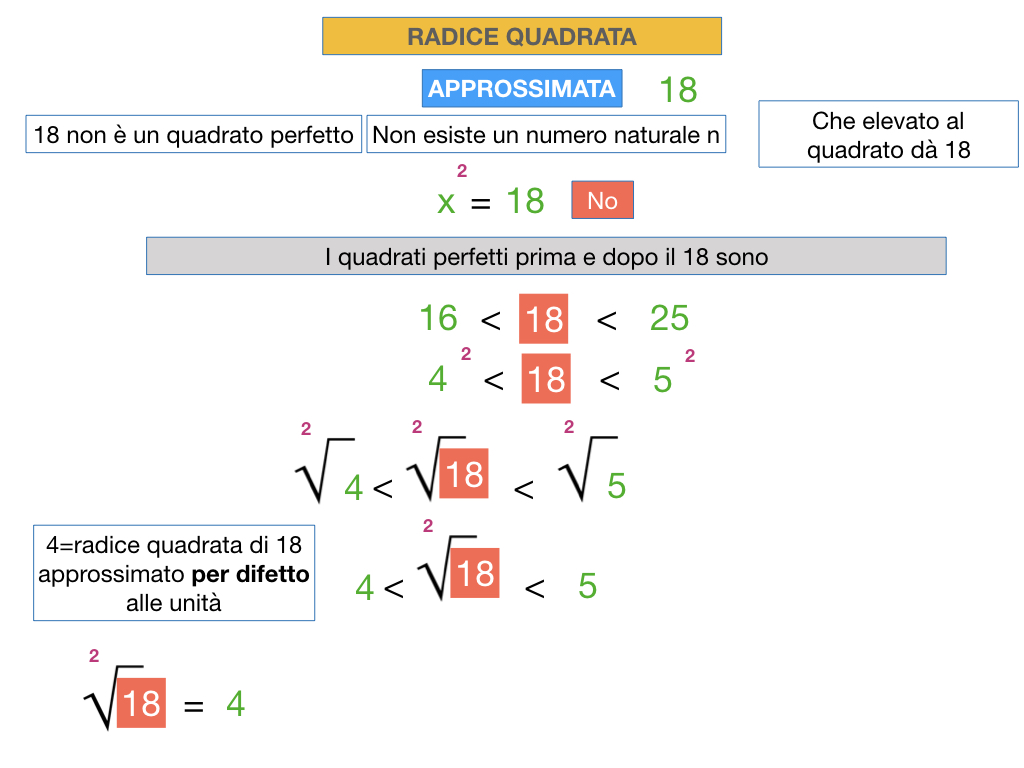
Radice quadrata di 18:
- Quadrato perfetto più vicino (inferiore): 16
- Radice quadrata di 16: 4
- Stima decimale:
  - 4.1 * 4.1 = 16.81 (inferiore a 18)
  - 4.2 * 4.2 = 17.64 (inferiore a 18)
  - 4.3 * 4.3 = 18.49 (superiore a 18)
  Quindi, 4.2 è una buona approssimazione per difetto.
Radice quadrata di 50:
- Quadrato perfetto più vicino (inferiore): 49
- Radice quadrata di 49: 7
- Stima decimale:
  - 7.0 * 7.0 = 49 (inferiore a 50)
  - 7.1 * 7.1 = 50.41 (superiore a 50)
  Quindi, 7.0 è una buona approssimazione per difetto.
Radice quadrata di 8:
- Quadrato perfetto più vicino (inferiore): 4
- Radice quadrata di 4: 2
- Stima decimale:
  - 2.8 * 2.8 = 7.84 (inferiore a 8)
  - 2.9 * 2.9 = 8.41 (superiore a 8)
  Quindi, 2.8 è una buona approssimazione per difetto.

Consigli Utili

Pratica: Più ti eserciti, più velocemente diventerai a stimare le radici quadrate.
Conosci i quadrati perfetti: Avere una buona conoscenza dei quadrati perfetti (1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144...) ti aiuterà a velocizzare il primo passo.
Non aver paura di provare: Non c'è niente di male nel provare diversi decimali. Ricorda, stai cercando un'approssimazione *per difetto*, quindi è meglio essere un po' più conservativi nella tua stima.
Usa l'intuizione: Man mano che ti eserciti, svilupperai un'intuizione migliore per i numeri e sarai in grado di stimare le radici quadrate in modo più accurato.
Ragiona per intervalli: Pensa a quale intervallo si trova il numero. Per esempio, sapendo che 4²=16 e 5²=25, la radice quadrata di 20 sarà tra 4 e 5.

Perché è utile saper approssimare le radici quadrate?

Saper approssimare le radici quadrate è un'abilità preziosa in molte situazioni:

Vita quotidiana: Quando fai giardinaggio, cucini o fai dei lavoretti in casa, potresti aver bisogno di stimare rapidamente delle lunghezze o delle aree. Conoscere questo metodo ti permetterà di fare stime più accurate senza bisogno di una calcolatrice.
Matematica: Questo metodo ti aiuta a sviluppare una comprensione più profonda dei numeri e delle loro relazioni. Ti aiuta anche a migliorare le tue capacità di calcolo mentale.
Scienze: In fisica e chimica, spesso è necessario calcolare rapidamente delle radici quadrate per risolvere dei problemi. Questo metodo ti può aiutare a fare stime veloci e accurate.
Preparazione agli esami: Molti esami, come il test d'ammissione all'università, richiedono di saper calcolare rapidamente delle radici quadrate. Conoscere questo metodo ti darà un vantaggio.

Conclusione

Imparare ad approssimare la radice quadrata per difetto a meno di 0.1 è un'abilità utile e gratificante. Con la pratica, diventerai sempre più bravo a fare queste stime mentalmente, il che ti aiuterà a sviluppare un intuito più forte per i numeri e a risolvere problemi in modo più efficiente. Ricorda, la chiave è la pratica costante e la comprensione dei concetti fondamentali. Non aver paura di sperimentare e di commettere errori: ogni errore è un'opportunità per imparare e migliorare. Speriamo che questo articolo ti sia stato utile e che ti incoraggi a esplorare ulteriormente il meraviglioso mondo della matematica! Metti in pratica quanto hai imparato e scopri quanto velocemente puoi migliorare! Buon calcolo!