Quarto Criterio Di Congruenza Dei Triangoli Rettangoli

In geometria, la congruenza è un concetto fondamentale che ci permette di stabilire quando due figure geometriche sono esattamente identiche, a meno di una traslazione, rotazione o riflessione. Nel caso specifico dei triangoli, esistono diversi criteri che ci consentono di determinare la congruenza basandoci su informazioni limitate, come la lunghezza dei lati o l'ampiezza degli angoli. Questo articolo si concentra su uno di questi criteri, specificamente applicabile ai triangoli rettangoli: il Quarto Criterio di Congruenza.

Il Quarto Criterio di Congruenza dei Triangoli Rettangoli: Una Panoramica

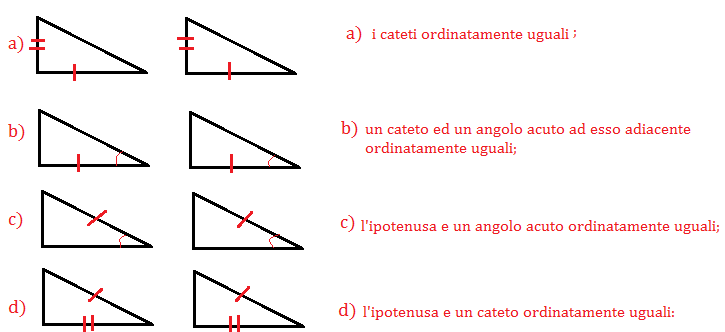
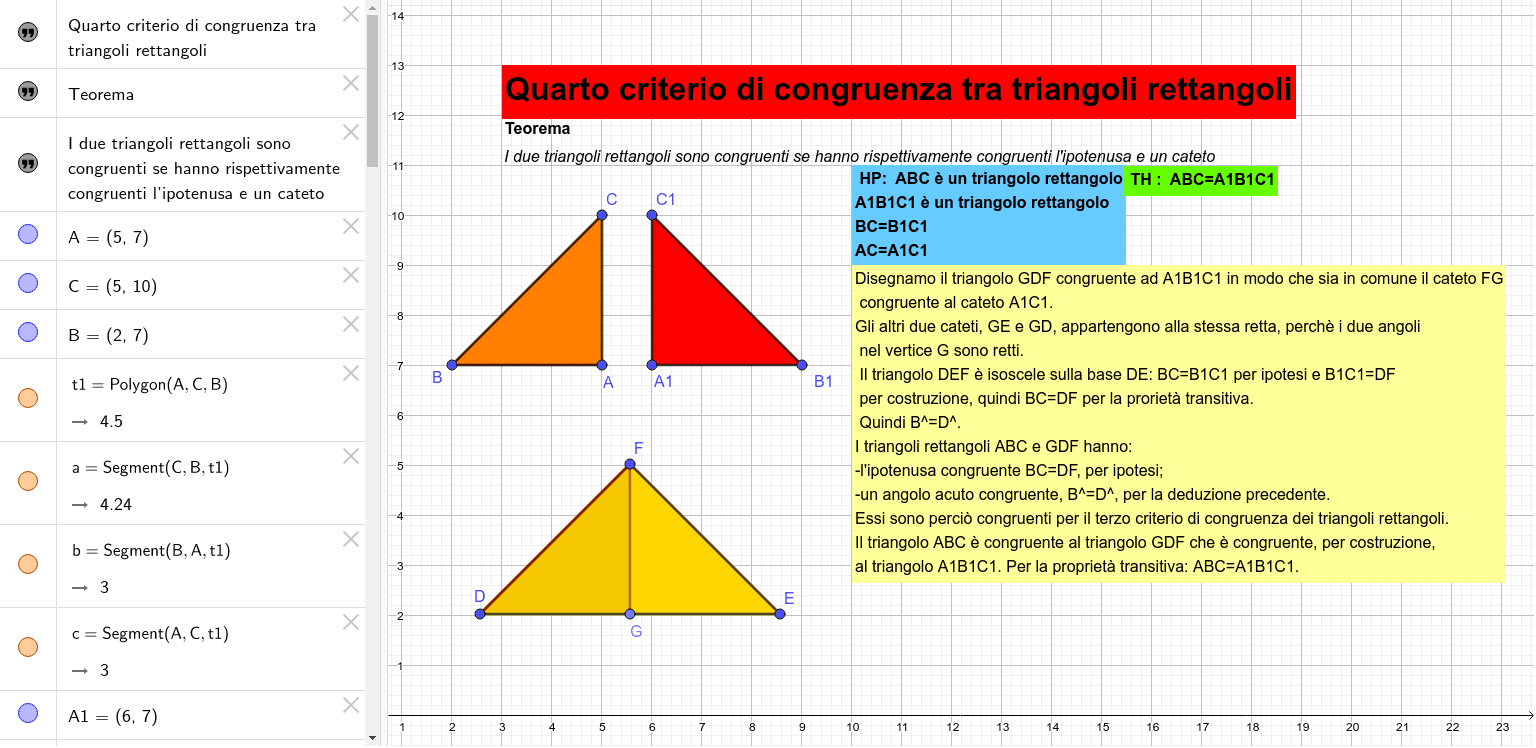
Il Quarto Criterio di Congruenza dei Triangoli Rettangoli afferma che due triangoli rettangoli sono congruenti se hanno rispettivamente congruenti un cateto e l'angolo acuto opposto a quel cateto.

In altre parole, se conosciamo la lunghezza di un cateto e l'ampiezza dell'angolo acuto che si trova di fronte a quel cateto in due triangoli rettangoli, e questi valori corrispondono nei due triangoli, allora possiamo concludere che i due triangoli sono identici, ossia congruenti.

Argomentazione del Criterio

Per comprendere la validità di questo criterio, è utile richiamare i concetti fondamentali di geometria e gli altri criteri di congruenza già noti.

Ricordiamo innanzitutto che in un triangolo rettangolo, uno degli angoli è di 90 gradi (l'angolo retto). Inoltre, la somma degli angoli interni di qualsiasi triangolo è sempre 180 gradi. Di conseguenza, se conosciamo l'angolo retto (90 gradi) e un altro angolo acuto in un triangolo rettangolo, possiamo facilmente calcolare il terzo angolo (il secondo angolo acuto) semplicemente sottraendo la somma dei due angoli noti da 180 gradi.

Quindi, se abbiamo due triangoli rettangoli in cui un cateto e l'angolo acuto opposto a quel cateto sono congruenti, possiamo dedurre che anche il secondo angolo acuto è congruente. A questo punto, abbiamo due angoli e un lato congruenti tra i due triangoli.

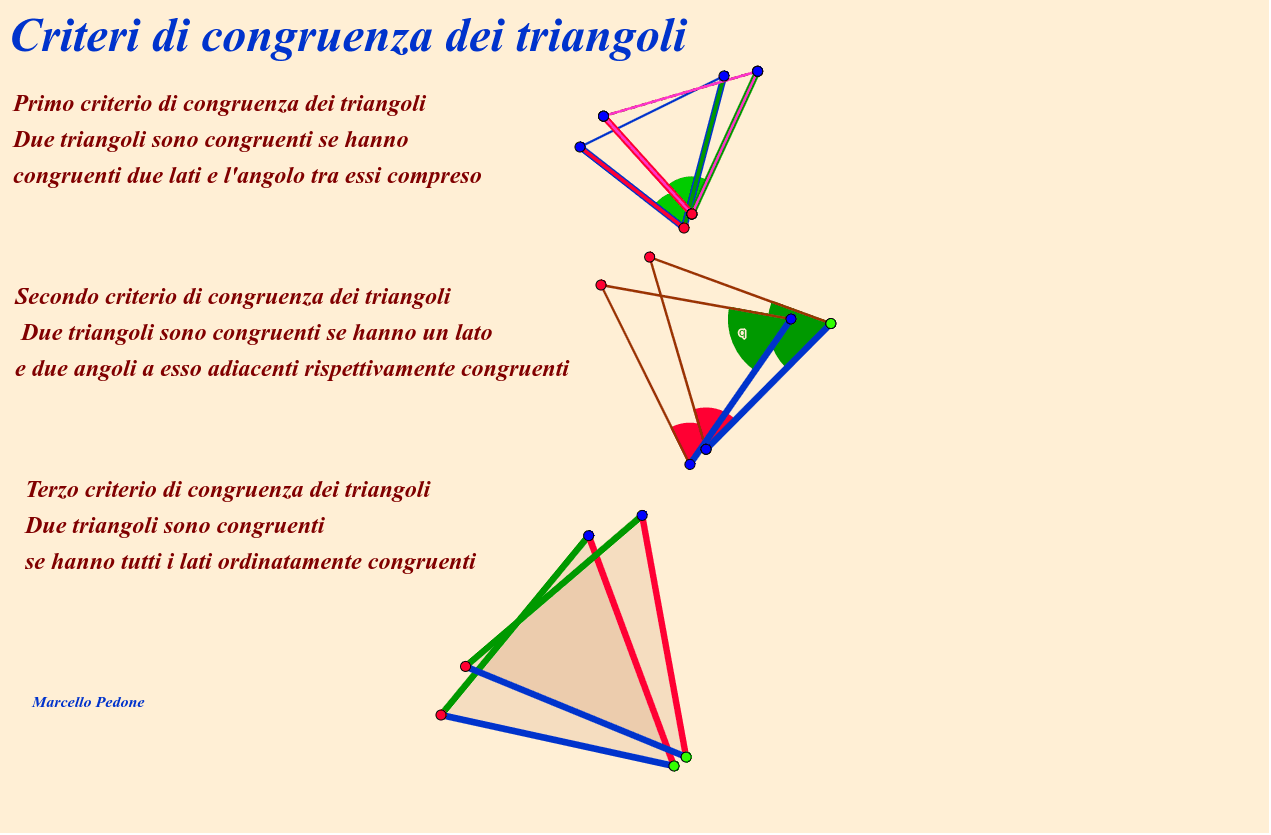
Possiamo ora richiamare il Secondo Criterio di Congruenza dei Triangoli (detto anche criterio ALA - Angolo-Lato-Angolo), che afferma che due triangoli sono congruenti se hanno rispettivamente congruenti due angoli e il lato compreso tra essi.

Nel nostro caso, abbiamo due angoli congruenti e il lato (il cateto) opposto a uno di questi angoli. Tuttavia, possiamo facilmente dimostrare che anche il lato compreso tra i due angoli è congruente. Consideriamo il cateto *a* e l'angolo acuto *α* opposto ad *a* in entrambi i triangoli. Abbiamo già stabilito che *a* è congruente e *α* è congruente. Sappiamo anche che l'angolo retto è congruente per definizione (entrambi sono angoli retti). Quindi, il lato compreso tra l'angolo retto e l'angolo acuto *α* è il cateto adiacente all'angolo *α*. Usando le relazioni trigonometriche (tangente), possiamo esprimere la lunghezza di questo cateto adiacente in termini del cateto *a* e dell'angolo *α*. Poiché *a* e *α* sono congruenti, anche il cateto adiacente sarà congruente.

A questo punto, abbiamo due angoli e il lato compreso tra essi congruenti, e quindi possiamo applicare il Secondo Criterio di Congruenza dei Triangoli per concludere che i due triangoli rettangoli sono congruenti.

Esempio Pratico

Immaginiamo di dover costruire due rampe per skateboard identiche. Entrambe le rampe devono avere un angolo di salita di 30 gradi e l'altezza verticale (il cateto opposto all'angolo di 30 gradi) deve essere di 1 metro.

Abbiamo quindi due triangoli rettangoli, uno per ciascuna rampa. In entrambi i triangoli, l'angolo di salita (un angolo acuto) è di 30 gradi, e l'altezza verticale (il cateto opposto a questo angolo) è di 1 metro. Possiamo quindi applicare il Quarto Criterio di Congruenza dei Triangoli Rettangoli e concludere che i due triangoli sono congruenti.

Questo significa che le due rampe saranno esattamente identiche, garantendo che gli skateboarder abbiano la stessa esperienza su entrambe le rampe.

Applicazioni Reali

Il Quarto Criterio di Congruenza dei Triangoli Rettangoli trova applicazioni in diversi campi, tra cui:

• Architettura e Ingegneria: Nella progettazione di edifici, ponti e altre strutture, è fondamentale garantire che elementi strutturali identici siano effettivamente congruenti per assicurare la stabilità e la sicurezza.
• Topografia: Nella misurazione del terreno e nella creazione di mappe, i triangoli rettangoli vengono spesso utilizzati per calcolare distanze e altezze. Il Quarto Criterio può essere utilizzato per verificare la congruenza di questi triangoli e garantire l'accuratezza delle misurazioni.
• Robotica: Nella progettazione di robot e sistemi automatizzati, è spesso necessario creare componenti identici. Il Quarto Criterio può essere utilizzato per verificare la congruenza di questi componenti.
• Produzione Industriale: Nel controllo qualità dei processi produttivi, il Quarto Criterio può essere applicato per verificare che i pezzi prodotti siano identici.

Limitazioni

È importante notare che il Quarto Criterio di Congruenza dei Triangoli Rettangoli si applica solo ai triangoli rettangoli. Non può essere utilizzato per dimostrare la congruenza di triangoli non rettangoli. Inoltre, è fondamentale che il cateto e l'angolo acuto opposto siano effettivamente congruenti in entrambi i triangoli per poter applicare il criterio. Se solo uno dei due è congruente, non si può concludere che i triangoli siano congruenti.

Conclusione

Il Quarto Criterio di Congruenza dei Triangoli Rettangoli è uno strumento potente e utile per dimostrare la congruenza di triangoli rettangoli. La sua semplicità e la sua applicabilità in diversi contesti lo rendono un concetto fondamentale nella geometria e in altre discipline scientifiche e ingegneristiche. Comprendere a fondo questo criterio e saperlo applicare correttamente può semplificare notevolmente la risoluzione di problemi geometrici e garantire la precisione in diverse applicazioni pratiche.

Invitiamo il lettore a esercitarsi con diversi esempi per acquisire una solida padronanza del Quarto Criterio di Congruenza dei Triangoli Rettangoli. La comprensione di questo e degli altri criteri di congruenza è essenziale per progredire nello studio della geometria e delle sue applicazioni.