Quanto Misurano Gli Angoli Di Un Triangolo Rettangolo

Un triangolo rettangolo è una figura geometrica fondamentale, presente in innumerevoli applicazioni pratiche e teoriche. La sua caratteristica distintiva è la presenza di un angolo retto, ovvero un angolo che misura esattamente 90 gradi. Ma cosa sappiamo degli altri due angoli di un triangolo rettangolo? Come si relazionano tra loro e con l'angolo retto? Questo articolo esplorerà in dettaglio le proprietà degli angoli di un triangolo rettangolo, fornendo una comprensione chiara e precisa del loro comportamento.

La Somma degli Angoli Interni di un Triangolo

Prima di addentrarci specificamente nei triangoli rettangoli, è cruciale ricordare un principio fondamentale della geometria euclidea: la somma degli angoli interni di qualsiasi triangolo è sempre pari a 180 gradi. Questo vale indipendentemente dalla forma o dalle dimensioni del triangolo. Che si tratti di un triangolo equilatero, isoscele, scaleno o rettangolo, la somma dei suoi tre angoli interni sarà invariabilmente 180 gradi. Questa proprietà è la chiave per comprendere le relazioni tra gli angoli di un triangolo rettangolo.

Angoli Acuti in un Triangolo Rettangolo

Dato che un triangolo rettangolo possiede un angolo di 90 gradi, gli altri due angoli devono necessariamente essere acuti, ovvero minori di 90 gradi. Questo deriva direttamente dal principio che la somma degli angoli interni deve essere 180 gradi. Se uno degli angoli è 90 gradi, la somma degli altri due deve essere 180 - 90 = 90 gradi. Di conseguenza, nessuno dei due angoli rimanenti può essere maggiore o uguale a 90 gradi, altrimenti la somma totale supererebbe i 180 gradi.

Definizione: Un angolo acuto è un angolo la cui misura è compresa tra 0 e 90 gradi.

Pertanto, in un triangolo rettangolo, abbiamo sempre un angolo retto (90 gradi) e due angoli acuti la cui somma è 90 gradi. Questi due angoli acuti sono detti angoli complementari.

Relazione tra gli Angoli Acuti

Gli angoli acuti di un triangolo rettangolo sono quindi complementari. Questo significa che la somma delle loro misure è esattamente 90 gradi. Se chiamiamo α e β i due angoli acuti, possiamo scrivere:

α + β = 90°

Conoscere la misura di uno degli angoli acuti permette di calcolare facilmente la misura dell'altro. Ad esempio, se un angolo acuto misura 30 gradi, l'altro angolo acuto misurerà 90 - 30 = 60 gradi.

Esempi Pratici e Applicazioni

I triangoli rettangoli e le loro proprietà angolari trovano un'ampia applicazione in diversi campi:

• Architettura e Ingegneria: La progettazione di edifici, ponti e altre strutture spesso si basa sui principi della trigonometria, che a sua volta dipende dalle proprietà dei triangoli rettangoli. Ad esempio, nel calcolo delle pendenze dei tetti o nella stabilità delle costruzioni.
• Navigazione: I sistemi di navigazione, sia terrestri che marittimi, utilizzano triangoli rettangoli per determinare distanze e angoli, sfruttando le funzioni trigonometriche.
• Fisica: La scomposizione di vettori in componenti ortogonali (orizzontale e verticale) si basa sulla proiezione del vettore sui lati di un triangolo rettangolo. Questo è fondamentale nello studio del moto dei proiettili, delle forze e di altri fenomeni fisici.
• Geometria: Lo studio delle figure geometriche, specialmente quelle basate su coordinate cartesiane, spesso coinvolge l'utilizzo di triangoli rettangoli per calcolare distanze, aree e volumi.

Esempio Numerico

Immaginiamo di dover costruire una rampa per sedie a rotelle. La normativa spesso impone un'inclinazione massima. Supponiamo che l'angolo di inclinazione massimo consentito sia di 5 gradi rispetto all'orizzontale. Possiamo modellare la rampa come un triangolo rettangolo, dove l'angolo tra la rampa (ipotenusa) e il terreno (cateto adiacente) è di 5 gradi. L'angolo rimanente, tra la rampa e l'altezza verticale (cateto opposto), sarà di 90 - 5 = 85 gradi. Conoscere questi angoli è fondamentale per garantire che la rampa sia conforme alle normative e sicura per l'uso.

Il Teorema di Pitagora e gli Angoli

Sebbene il Teorema di Pitagora (a² + b² = c², dove a e b sono i cateti e c è l'ipotenusa) si concentri sulla relazione tra i lati di un triangolo rettangolo, indirettamente fornisce informazioni sugli angoli. La relazione tra i lati determina gli angoli e viceversa. Se conosciamo la lunghezza dei tre lati, possiamo utilizzare le funzioni trigonometriche inverse (arcoseno, arcocoseno, arcotangente) per calcolare gli angoli acuti del triangolo.

Come Calcolare gli Angoli con le Funzioni Trigonometriche

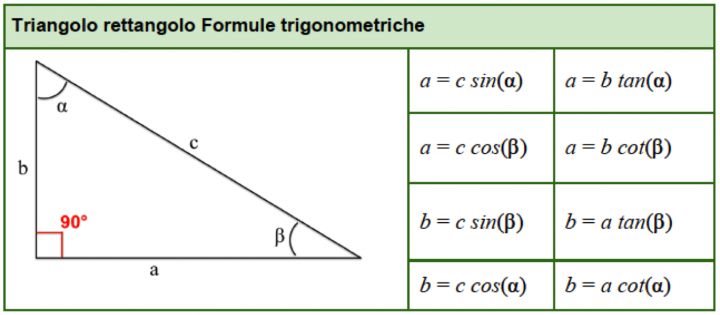
Le funzioni trigonometriche (seno, coseno e tangente) mettono in relazione gli angoli acuti di un triangolo rettangolo con i rapporti tra i suoi lati. Ad esempio:

• Seno (sin): sin(α) = cateto opposto / ipotenusa
• Coseno (cos): cos(α) = cateto adiacente / ipotenusa
• Tangente (tan): tan(α) = cateto opposto / cateto adiacente

Se conosciamo il rapporto tra due lati, possiamo utilizzare le funzioni trigonometriche inverse (arcsin, arccos, arctan) per trovare l'angolo. Ad esempio, se sappiamo che sin(α) = 0.5, allora α = arcsin(0.5) = 30 gradi.

Triangoli Rettangoli Speciali

Esistono alcuni triangoli rettangoli con angoli specifici che si incontrano frequentemente e che meritano una menzione particolare:

• Triangolo Rettangolo Isoscele (45-45-90): In questo triangolo, i due cateti sono uguali e gli angoli acuti sono entrambi di 45 gradi.
• Triangolo Rettangolo 30-60-90: Questo triangolo ha angoli di 30, 60 e 90 gradi. I suoi lati hanno proporzioni specifiche: l'ipotenusa è il doppio del cateto minore (opposto all'angolo di 30 gradi), e il cateto maggiore (opposto all'angolo di 60 gradi) è √3 volte il cateto minore.

La conoscenza delle proprietà di questi triangoli speciali può semplificare molti calcoli e risolvere problemi geometrici più rapidamente.

Conclusioni

In sintesi, in un triangolo rettangolo:

• Un angolo misura 90 gradi (angolo retto).
• Gli altri due angoli sono acuti (minori di 90 gradi).
• La somma dei due angoli acuti è di 90 gradi (angoli complementari).
• Le funzioni trigonometriche e il Teorema di Pitagora forniscono strumenti per calcolare gli angoli e i lati del triangolo.

Comprendere le relazioni tra gli angoli di un triangolo rettangolo è fondamentale per risolvere problemi di geometria, trigonometria e innumerevoli applicazioni pratiche. Invitiamo i lettori a esplorare ulteriormente le proprietà dei triangoli rettangoli e a sperimentare con diversi esempi per consolidare la loro comprensione.

Esercizio: Prova a disegnare diversi triangoli rettangoli e a misurare i loro angoli con un goniometro. Verifica che la somma degli angoli interni sia sempre di 180 gradi e che gli angoli acuti siano complementari. Utilizza le funzioni trigonometriche per calcolare gli angoli a partire dalla lunghezza dei lati e confronta i risultati con le misurazioni.