Quanto è La Somma Degli Angoli Interni Di Un Triangolo

Ti sei mai chiesto perché un triangolo è così fondamentale in geometria? O perché è utilizzato in così tante costruzioni e design che ci circondano? Una delle sue proprietà più basiche, ma incredibilmente importanti, è la somma dei suoi angoli interni. Capire questo concetto non è solo utile per superare un esame di matematica, ma anche per apprezzare il modo in cui il mondo è costruito intorno a noi.

Perché Dovremmo Preoccuparci degli Angoli di un Triangolo?

Lo so, a volte la geometria può sembrare un esercizio astratto e distante dalla vita reale. Ma pensaci un attimo. Gli architetti utilizzano i triangoli per creare strutture stabili come ponti e grattacieli. I designer li impiegano per costruire mobili robusti. Persino gli artisti li sfruttano per creare composizioni visivamente piacevoli. La somma degli angoli interni di un triangolo è un mattone fondamentale per costruire una miriade di cose che diamo per scontate.

Immagina di dover costruire una casetta sull'albero. Se gli angoli dei triangoli che utilizzi per la struttura non sono corretti, la casetta potrebbe essere instabile e pericolosa. Oppure, pensa a un navigatore che utilizza la triangolazione per determinare la propria posizione: una comprensione errata degli angoli potrebbe portarlo fuori rotta. In breve, la conoscenza di questo concetto ha un impatto reale sulla nostra vita quotidiana, anche se non ce ne rendiamo conto.

La Risposta: La Somma Magica è 180 Gradi

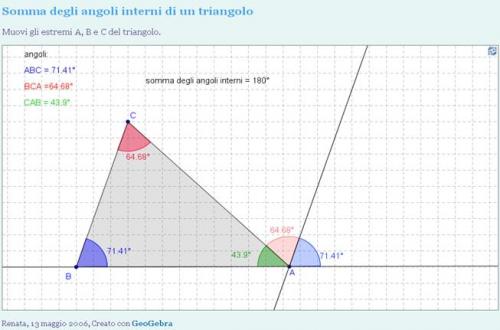
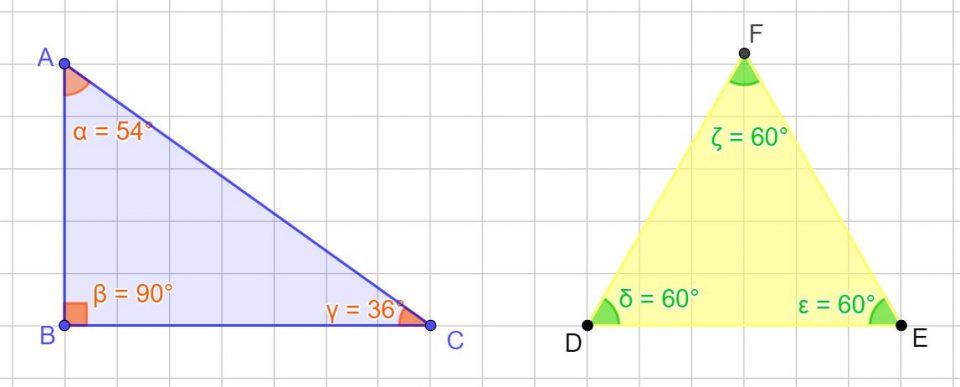
Allora, qual è la risposta? La somma degli angoli interni di un triangolo è sempre 180 gradi. Che si tratti di un triangolo equilatero (con tutti gli angoli uguali a 60 gradi), un triangolo isoscele (con due angoli uguali) o un triangolo scaleno (con tutti gli angoli diversi), la somma dei suoi angoli interni sarà sempre 180 gradi. Questo è un assioma fondamentale della geometria euclidea.

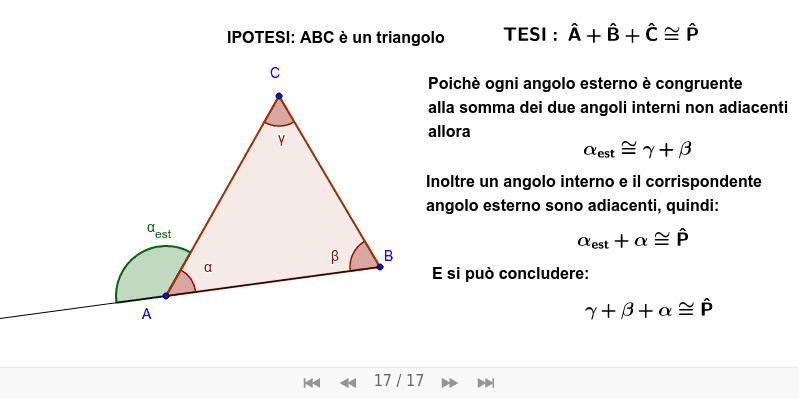
Come Dimostrare Questa Regola?

Esistono diversi modi per dimostrare questa regola. Uno dei più semplici e intuitivi è il seguente:

• Disegna un triangolo su un foglio di carta.
• Strappa via i tre angoli del triangolo.
• Allinea i tre angoli strappati in modo che i loro vertici si tocchino.
• Osserva che i tre angoli formano un angolo piatto, che equivale a 180 gradi.

Questo semplice esperimento dimostra visivamente che la somma degli angoli interni di un triangolo è effettivamente 180 gradi.

Affrontare le Controargomentazioni

Potresti chiederti: "Ma cosa succede se non ci troviamo nella geometria euclidea?". È una domanda valida! In geometrie non euclidee, come la geometria sferica (immagina la superficie di un pallone da calcio), la somma degli angoli interni di un triangolo può essere superiore a 180 gradi. Questo perché la superficie è curva, e le linee rette (o meglio, le geodetiche, che sono i percorsi più brevi tra due punti sulla superficie) si comportano in modo diverso.

Tuttavia, nella geometria euclidea, che è quella con cui abbiamo più familiarità e che utilizziamo nella maggior parte delle applicazioni pratiche, la somma degli angoli interni di un triangolo è sempre 180 gradi. Quindi, per il contesto di questo articolo, ci concentriamo sulla geometria euclidea.

Esempi Pratici e Risoluzione di Problemi

Vediamo come possiamo utilizzare questa conoscenza per risolvere problemi pratici:

Esempio 1: Supponiamo di avere un triangolo in cui due angoli misurano rispettivamente 60 gradi e 80 gradi. Qual è la misura del terzo angolo?

Soluzione: Sappiamo che la somma degli angoli interni deve essere 180 gradi. Quindi, sottraiamo la somma dei due angoli conosciuti (60 + 80 = 140) da 180: 180 - 140 = 40. Pertanto, il terzo angolo misura 40 gradi.

Esempio 2: Abbiamo un triangolo rettangolo in cui uno degli angoli acuti misura 30 gradi. Qual è la misura dell'altro angolo acuto?

Soluzione: Un triangolo rettangolo ha un angolo di 90 gradi. Quindi, abbiamo un angolo di 90 gradi e un angolo di 30 gradi. La loro somma è 120 gradi. Sottraiamo questa somma da 180: 180 - 120 = 60. Pertanto, l'altro angolo acuto misura 60 gradi.

L'Importanza della Pratica

Come per qualsiasi concetto matematico, la pratica è fondamentale per padroneggiare la somma degli angoli interni di un triangolo. Prova a risolvere diversi esercizi e problemi. Più ti eserciti, più diventerà intuitivo e naturale applicare questa regola.

Consigli per la Pratica:

• Utilizza risorse online: Ci sono molti siti web e app che offrono esercizi e quiz sulla geometria.
• Consulta il tuo libro di testo: Il tuo libro di testo di matematica conterrà sicuramente esercizi e problemi sulla somma degli angoli interni di un triangolo.
• Chiedi aiuto al tuo insegnante: Se hai difficoltà, non esitare a chiedere aiuto al tuo insegnante.
• Lavora con i tuoi compagni di classe: Studiare e risolvere problemi insieme ai tuoi compagni di classe può essere un modo efficace per imparare.

Un Concetto Semplice con Implicazioni Profonde

La somma degli angoli interni di un triangolo può sembrare un concetto semplice, ma ha implicazioni profonde in molti campi, dalla geometria all'architettura all'ingegneria. Comprendere questa regola fondamentale ti aprirà le porte a una comprensione più profonda del mondo che ti circonda.

Ricorda, la geometria non è solo un insieme di regole e formule astratte. È un modo di pensare, un modo di vedere il mondo. E la somma degli angoli interni di un triangolo è una piccola finestra su questo mondo affascinante.

Quindi, la prossima volta che vedi un triangolo, fermati un attimo a pensare agli angoli che lo compongono. Pensa alla loro somma, e pensa a come questo semplice concetto ha contribuito a costruire il mondo che conosciamo.

Un Passo Avanti: Triangoli e il Mondo Reale

Oltre alle applicazioni già menzionate, i triangoli e la loro proprietà degli angoli interni giocano un ruolo cruciale in diverse altre aree:

• Navigazione e Cartografia: La triangolazione è una tecnica fondamentale per determinare la posizione e creare mappe accurate. I navigatori, i geografi e persino le app GPS utilizzano i triangoli per calcolare distanze e posizioni.
• Astronomia: Gli astronomi usano la parallasse, una tecnica basata sui triangoli, per misurare la distanza dalle stelle. La parallasse sfrutta il cambiamento apparente nella posizione di una stella vista da due punti di osservazione diversi (ad esempio, la Terra in due posizioni opposte della sua orbita).
• Fotografia e Grafica Computerizzata: I triangoli sono gli elementi fondamentali utilizzati per creare modelli 3D in grafica computerizzata. La loro semplicità e la loro prevedibilità li rendono ideali per rappresentare superfici complesse.
• Design di Strutture: Come già detto, i triangoli sono incredibilmente resistenti e vengono utilizzati in una vasta gamma di strutture, dai ponti alle torri eoliche. La loro forma distribuisce le forze in modo uniforme, rendendoli molto più stabili di altre forme geometriche.

Questi sono solo alcuni esempi di come la semplice idea della somma degli angoli interni di un triangolo si manifesti nel mondo reale. Più impari, più inizi a vedere i triangoli ovunque!

Ora, ripensa a un progetto o un problema che hai affrontato di recente. Riesci a identificare dove la conoscenza degli angoli di un triangolo avrebbe potuto esserti utile? Quali nuove prospettive hai acquisito su questo concetto fondamentale?