Quando Due Grandezze Sono Direttamente Proporzionali

Hai mai notato come alcune cose aumentano o diminuiscono insieme, mantenendo un certo equilibrio? Pensa a quando compri più pane: più ne compri, più spendi. Questa relazione, apparentemente semplice, è alla base di un concetto matematico fondamentale: la proporzionalità diretta. Questo articolo è pensato per tutti, dagli studenti delle medie fino a chi semplicemente vuole rispolverare le proprie conoscenze di matematica. Esploreremo cosa significa esattamente che due grandezze siano direttamente proporzionali, come possiamo identificarle e come possiamo utilizzarle per risolvere problemi concreti.
Cosa Significa "Direttamente Proporzionale"?
Due grandezze si dicono direttamente proporzionali se all'aumentare di una, anche l'altra aumenta in modo tale che il loro rapporto rimanga costante. In altre parole, se una grandezza raddoppia, anche l'altra raddoppia; se una triplica, anche l'altra triplica, e così via. Allo stesso modo, se una si dimezza, anche l'altra si dimezza.
La Chiave: Il Rapporto Costante
L'elemento cruciale è proprio questa costanza del rapporto. Immagina di avere due grandezze, chiamiamole x e y. Se y è direttamente proporzionale a x, allora esiste un numero k (diverso da zero) tale che:
y / x = k
Questo numero k è chiamato costante di proporzionalità. Possiamo anche scrivere questa relazione in un altro modo:
y = k * x
Questa equazione ci dice che il valore di y è sempre uguale al valore di x moltiplicato per la costante k.
Esempi Pratici di Proporzionalità Diretta
Per rendere il concetto più chiaro, vediamo alcuni esempi concreti tratti dalla vita di tutti i giorni:
- Il prezzo e la quantità: Come accennato prima, il prezzo totale di un prodotto è direttamente proporzionale alla quantità acquistata (se il prezzo unitario rimane costante). Più compri, più spendi.
- La velocità e la distanza (a tempo costante): Se viaggi a una velocità costante, la distanza percorsa è direttamente proporzionale al tempo impiegato. Più viaggi velocemente, più strada fai nello stesso tempo.
- Il numero di ingredienti e le porzioni: In una ricetta, il numero di ingredienti è direttamente proporzionale al numero di porzioni che si vogliono preparare. Se vuoi preparare più porzioni, devi aumentare proporzionalmente la quantità di ogni ingrediente.
- Il peso e il volume (per una stessa sostanza): Per una data sostanza, il peso è direttamente proporzionale al volume. Più volume hai, più pesa (ad esempio, più acqua hai, più pesa).
Un Esempio Dettagliato: La Ricetta della Torta
Immagina di avere una ricetta per una torta che richiede 2 uova, 100g di farina e 80g di zucchero. Se vuoi preparare una torta più grande, che sia il doppio di quella originale, dovrai raddoppiare le quantità di tutti gli ingredienti. Avrai bisogno di 4 uova, 200g di farina e 160g di zucchero. La relazione tra il numero di torte e la quantità di ogni ingrediente è una proporzionalità diretta. La costante di proporzionalità, in questo caso, dipende dall'ingrediente specifico. Ad esempio, per le uova, la costante di proporzionalità è 2 uova per torta originale; per la farina, è 100g di farina per torta originale, e così via.
Come Identificare la Proporzionalità Diretta
Esistono diversi modi per verificare se due grandezze sono direttamente proporzionali:
- Osservare la relazione: Se all'aumentare di una grandezza, l'altra aumenta in modo simile (raddoppia quando l'altra raddoppia, etc.), allora è probabile che ci sia una proporzionalità diretta.
- Calcolare il rapporto: Prendi diverse coppie di valori delle due grandezze e calcola il rapporto tra di esse. Se il rapporto è sempre lo stesso (cioè, è costante), allora le grandezze sono direttamente proporzionali.
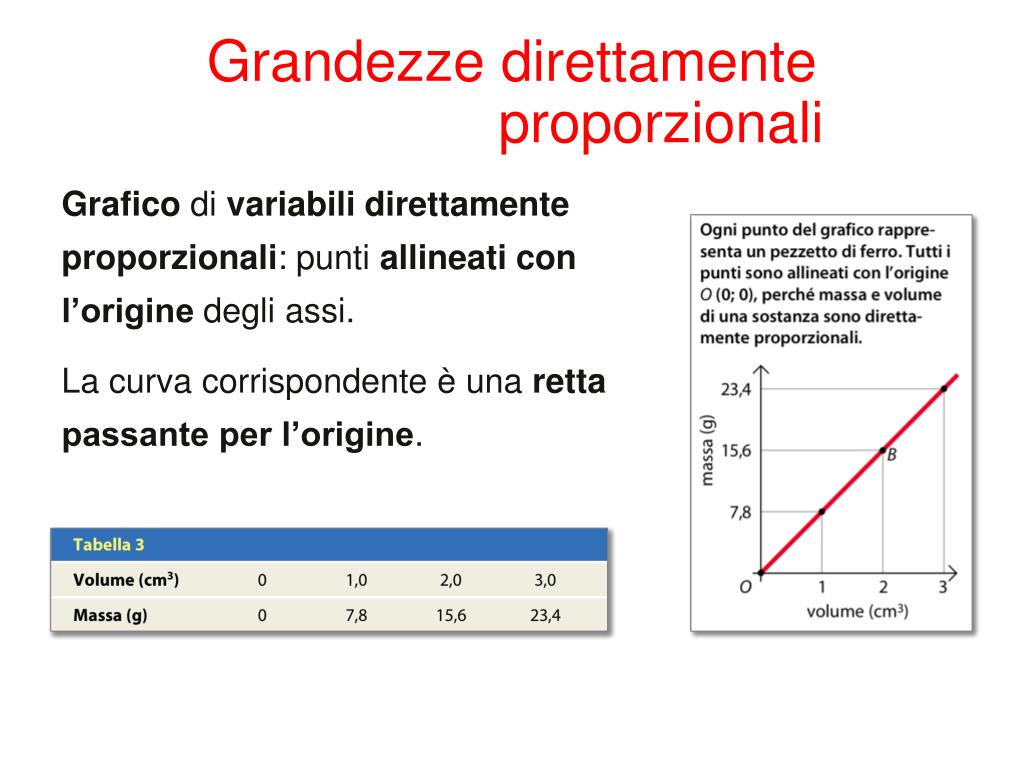
- Grafico: Se rappresenti graficamente le due grandezze su un piano cartesiano, i punti dovrebbero allinearsi su una retta che passa per l'origine (il punto (0,0)).
Esempio: Verificare la Proporzionalità Diretta con il Rapporto
Supponiamo di avere i seguenti dati relativi al numero di ore lavorate e allo stipendio ricevuto:
- 4 ore lavorate -> 40 euro
- 8 ore lavorate -> 80 euro
- 12 ore lavorate -> 120 euro
Calcoliamo il rapporto tra lo stipendio e le ore lavorate in ciascun caso:
- 40 euro / 4 ore = 10 euro/ora
- 80 euro / 8 ore = 10 euro/ora
- 120 euro / 12 ore = 10 euro/ora
Poiché il rapporto è sempre lo stesso (10 euro/ora), possiamo concludere che lo stipendio è direttamente proporzionale al numero di ore lavorate, e la costante di proporzionalità è 10 (che rappresenta la paga oraria).
Utilizzare la Proporzionalità Diretta per Risolvere Problemi
La proporzionalità diretta è uno strumento molto utile per risolvere problemi di vario tipo. Vediamo alcuni esempi:
Problema 1: Il Costo della Benzina
Se 10 litri di benzina costano 15 euro, quanto costeranno 25 litri?
Soluzione: Sappiamo che il costo della benzina è direttamente proporzionale alla quantità di litri acquistati. Possiamo impostare una proporzione:
10 litri / 15 euro = 25 litri / x euro
Risolvendo per x (il costo di 25 litri), otteniamo:
x = (25 litri * 15 euro) / 10 litri = 37.5 euro
Quindi, 25 litri di benzina costeranno 37.5 euro.
Problema 2: La Scala di una Mappa
Su una mappa, 2 cm rappresentano 5 km nella realtà. Se due città distano 8 cm sulla mappa, qual è la distanza reale tra le due città?
Soluzione: La distanza sulla mappa è direttamente proporzionale alla distanza reale. Impostiamo la proporzione:
2 cm / 5 km = 8 cm / x km
Risolvendo per x (la distanza reale), otteniamo:
x = (8 cm * 5 km) / 2 cm = 20 km
Quindi, la distanza reale tra le due città è di 20 km.
Un Concetto Fondamentale con Molte Applicazioni
La proporzionalità diretta è un concetto fondamentale in matematica e nelle scienze, con innumerevoli applicazioni pratiche. Comprendere questo concetto ti permetterà di risolvere problemi in diversi contesti, dalla spesa al supermercato alla pianificazione di un viaggio. Imparare a riconoscere le relazioni di proporzionalità diretta ti fornirà un potente strumento per interpretare il mondo che ti circonda e prendere decisioni informate.
Ricorda:
- La proporzionalità diretta implica un rapporto costante tra due grandezze.
- Puoi verificare la proporzionalità diretta calcolando il rapporto tra le grandezze o osservando la relazione tra i loro valori.
- La proporzionalità diretta è utile per risolvere problemi di vario tipo, impostando proporzioni e calcolando valori sconosciuti.
Speriamo che questo articolo ti abbia aiutato a comprendere meglio il concetto di proporzionalità diretta. Continua a esplorare e applicare questa conoscenza nella tua vita quotidiana!