Qual è Lo Spigolo Di Un Cubo

Ti sei mai fermato a osservare attentamente un cubo? Magari un dado, un regalo impacchettato o un blocco da costruzione? Probabilmente lo dai per scontato, ma dietro la sua forma semplice si nasconde una precisione matematica affascinante. Una delle caratteristiche fondamentali di un cubo è proprio lo spigolo. Ma cos'è esattamente uno spigolo e come lo calcoliamo?

In questo articolo, esploreremo a fondo il concetto di spigolo di un cubo, partendo dalle basi e arrivando a concetti più avanzati. Cercheremo di rendere tutto chiaro e accessibile, senza usare termini complicati, per aiutarti a capire a fondo questa importante proprietà geometrica.

Che cos'è uno Spigolo?

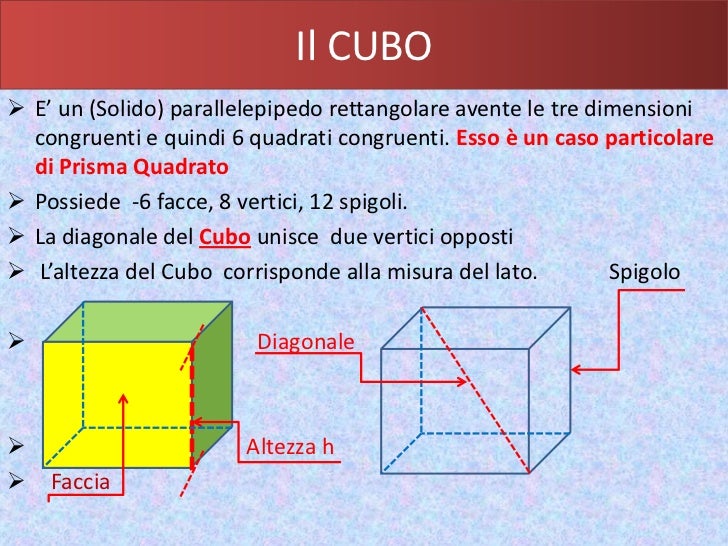
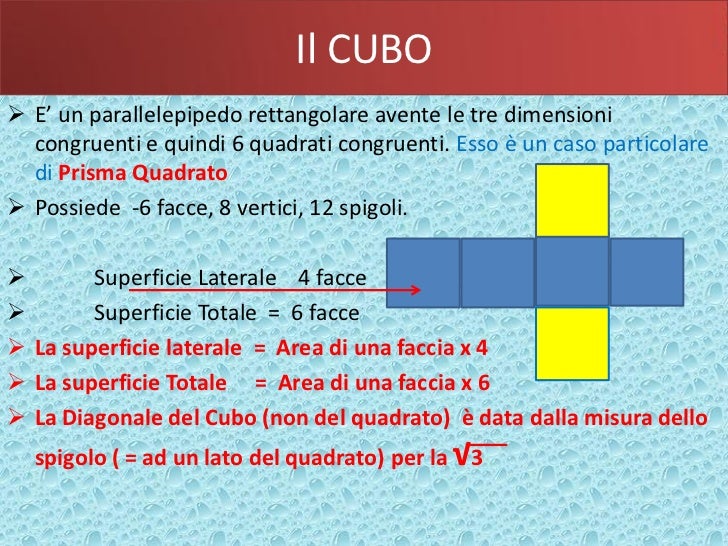
Immagina di tenere in mano un cubo. Vedrai che è composto da diverse facce, tutte perfettamente quadrate. Ora, osserva come queste facce si incontrano. Dove due facce si incontrano, formano una linea. Questa linea è proprio lo spigolo del cubo. In termini geometrici, lo spigolo è il segmento di retta che delimita una faccia del solido. In altre parole, è il lato del quadrato che compone ogni faccia del cubo.

In sintesi: Lo spigolo è semplicemente il lato di un quadrato che forma una delle facce del cubo.

Un cubo ha 12 spigoli in totale. Questo perché ha 6 facce e ogni faccia ha 4 lati, ma ogni lato è condiviso da due facce. Quindi, (6 facce * 4 lati)/2 = 12 spigoli.

Come Calcolare lo Spigolo di un Cubo

Esistono diversi modi per calcolare la lunghezza dello spigolo di un cubo, a seconda di quali informazioni hai a disposizione. Vediamo i metodi più comuni:

1. Conoscendo l'Area di una Faccia

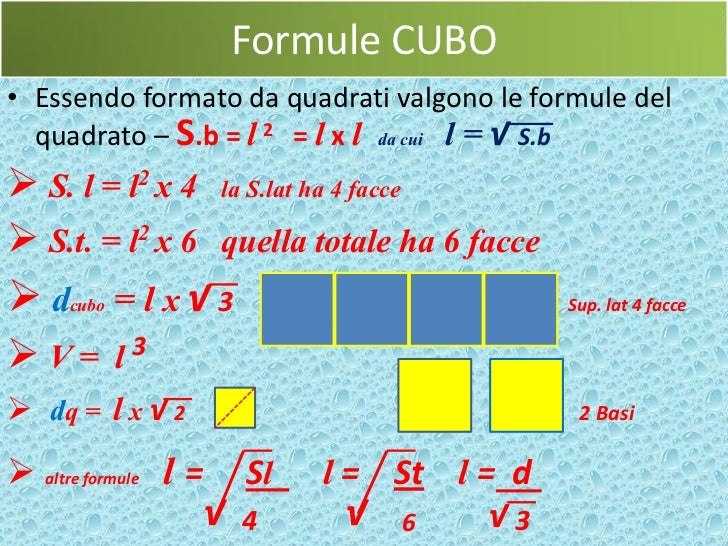
Se conosci l'area di una delle facce del cubo, il calcolo dello spigolo è molto semplice. Ricorda che ogni faccia è un quadrato e l'area di un quadrato si calcola elevando al quadrato la lunghezza del lato (Area = lato²). Quindi, per trovare lo spigolo, devi semplicemente calcolare la radice quadrata dell'area della faccia.

Formula: Spigolo = √Area

Esempio: Se l'area di una faccia del cubo è 25 cm², allora lo spigolo sarà √25 = 5 cm.

2. Conoscendo il Volume del Cubo

Il volume di un cubo si calcola elevando al cubo la lunghezza dello spigolo (Volume = spigolo³). Quindi, se conosci il volume, per trovare lo spigolo devi calcolare la radice cubica del volume.

Formula: Spigolo = ∛Volume

Esempio: Se il volume del cubo è 64 cm³, allora lo spigolo sarà ∛64 = 4 cm.

3. Conoscendo la Diagonale di una Faccia

La diagonale di un quadrato (la faccia del cubo) divide il quadrato in due triangoli rettangoli uguali. Possiamo quindi usare il teorema di Pitagora per trovare la relazione tra la diagonale e lo spigolo. Il teorema di Pitagora afferma che in un triangolo rettangolo, il quadrato dell'ipotenusa (la diagonale in questo caso) è uguale alla somma dei quadrati dei cateti (gli spigoli del quadrato). Quindi: diagonale² = spigolo² + spigolo² = 2 * spigolo²

Per trovare lo spigolo conoscendo la diagonale, dobbiamo quindi dividere il quadrato della diagonale per 2 e poi calcolare la radice quadrata del risultato.

Formula: Spigolo = √(diagonale² / 2)

Esempio: Se la diagonale di una faccia del cubo è 7.07 cm (circa), allora lo spigolo sarà √(7.07² / 2) = √(50 / 2) = √25 = 5 cm.

4. Conoscendo la Diagonale del Cubo (Spazio)

La diagonale del cubo (detta anche diagonale spaziale) è la linea che collega due vertici opposti del cubo, passando attraverso il suo interno. Anche in questo caso, possiamo usare il teorema di Pitagora, ma applicato in tre dimensioni. La relazione tra la diagonale spaziale e lo spigolo è: diagonale² = spigolo² + spigolo² + spigolo² = 3 * spigolo²

Per trovare lo spigolo conoscendo la diagonale spaziale, dobbiamo dividere il quadrato della diagonale per 3 e poi calcolare la radice quadrata del risultato.

Formula: Spigolo = √(diagonale² / 3)

Esempio: Se la diagonale spaziale del cubo è 8.66 cm (circa), allora lo spigolo sarà √(8.66² / 3) = √(75 / 3) = √25 = 5 cm.

Perché è Importante Conoscere lo Spigolo di un Cubo?

La conoscenza dello spigolo di un cubo è fondamentale in diversi contesti:

• Matematica e Geometria: È la base per calcolare altre proprietà del cubo come l'area totale della superficie, il volume e le diagonali.
• Ingegneria e Architettura: Nel design e nella costruzione di edifici e strutture, conoscere le dimensioni precise dei cubi o di oggetti cubici è essenziale per garantire la stabilità e la funzionalità.
• Packaging e Logistica: Il calcolo del volume di scatole cubiche o contenitori è cruciale per ottimizzare lo spazio durante il trasporto e lo stoccaggio di merci.
• Arte e Design: Gli artisti e i designer spesso utilizzano cubi come elementi base nelle loro creazioni, e la conoscenza dello spigolo è importante per mantenere le proporzioni corrette.

Inoltre, la comprensione delle relazioni tra spigolo, area, volume e diagonali aiuta a sviluppare il pensiero logico e le capacità di problem solving.

Esempi Pratici

Immagina di dover costruire una scatola cubica per un regalo. Sai che il regalo ha un volume di 125 cm³. Per costruire la scatola, devi conoscere la lunghezza dello spigolo. Usando la formula Spigolo = ∛Volume, calcoli che lo spigolo deve essere ∛125 = 5 cm. Ora sai esattamente quanto tagliare il cartone per costruire la scatola perfetta!

Oppure, immagina di dover calcolare la quantità di vernice necessaria per dipingere un cubo di legno. Misuri un lato (lo spigolo) e scopri che è lungo 10 cm. Sai che l'area totale della superficie di un cubo è 6 * spigolo². Quindi, l'area da dipingere è 6 * 10² = 600 cm². A questo punto, puoi calcolare la quantità di vernice necessaria in base alla sua copertura per centimetro quadrato.

Conclusione

Come abbiamo visto, lo spigolo è un elemento chiave per comprendere le proprietà geometriche di un cubo. Conoscere come calcolarlo, a partire da diverse informazioni, è utile in molti ambiti pratici e contribuisce a sviluppare il pensiero logico e le capacità di risoluzione dei problemi. Speriamo che questo articolo ti abbia chiarito ogni dubbio e ti abbia fornito gli strumenti per affrontare qualsiasi problema che coinvolga il calcolo dello spigolo di un cubo.

Ricorda: la geometria è ovunque intorno a noi! Prendersi il tempo per comprenderla può aprirti un mondo di possibilità e aiutarti a risolvere problemi inaspettati nella vita di tutti i giorni. Non sottovalutare mai la potenza di un semplice spigolo!