Qual è L'altezza Di Un Rombo

Calcolare l'altezza di un rombo può sembrare una sfida, ma in realtà è un processo accessibile se si comprendono i concetti fondamentali della geometria. Questa guida dettagliata esplorerà le diverse metodologie per determinare l'altezza di un rombo, fornendo spiegazioni chiare e esempi pratici.
Comprendere il Rombo e le Sue Proprietà
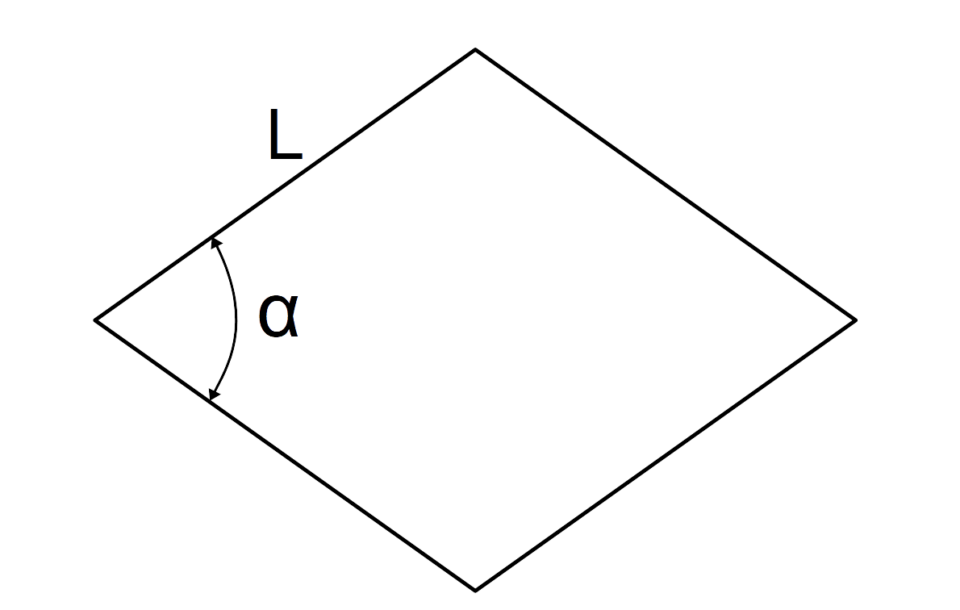
Prima di addentrarci nel calcolo dell'altezza, è essenziale definire cos'è un rombo e quali sono le sue caratteristiche principali. Un rombo è un quadrilatero con quattro lati di uguale lunghezza. Le sue diagonali si intersecano ad angolo retto, bisecandosi a vicenda. Inoltre, gli angoli opposti di un rombo sono congruenti.
Proprietà Chiave del Rombo:
- Lati: Tutti e quattro i lati sono di uguale lunghezza.
- Diagonali: Si intersecano perpendicolarmente e si bisecano.
- Angoli: Gli angoli opposti sono uguali.
- Area: Può essere calcolata in diversi modi (che vedremo in seguito).
Queste proprietà sono cruciali per comprendere come calcolare l'altezza, poiché forniscono le basi per le diverse formule e approcci.
Metodi per Calcolare l'Altezza di un Rombo
Esistono diversi metodi per calcolare l'altezza di un rombo, a seconda delle informazioni disponibili. Esploreremo i più comuni e utili.
1. Utilizzando l'Area e la Lunghezza del Lato
Il metodo più diretto è utilizzare la formula dell'area del rombo. Ricordiamo che l'area di un rombo può essere espressa come:
Area = base × altezza
Poiché tutti i lati di un rombo sono uguali, qualsiasi lato può essere considerato la base. Pertanto, se conosciamo l'area (A) e la lunghezza di un lato (l), possiamo calcolare l'altezza (h) con la seguente formula:
h = A / l
Esempio: Se un rombo ha un'area di 60 cm² e un lato di 10 cm, l'altezza sarà 60 cm² / 10 cm = 6 cm.
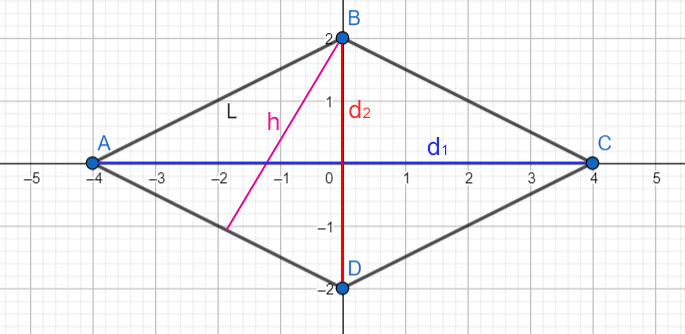
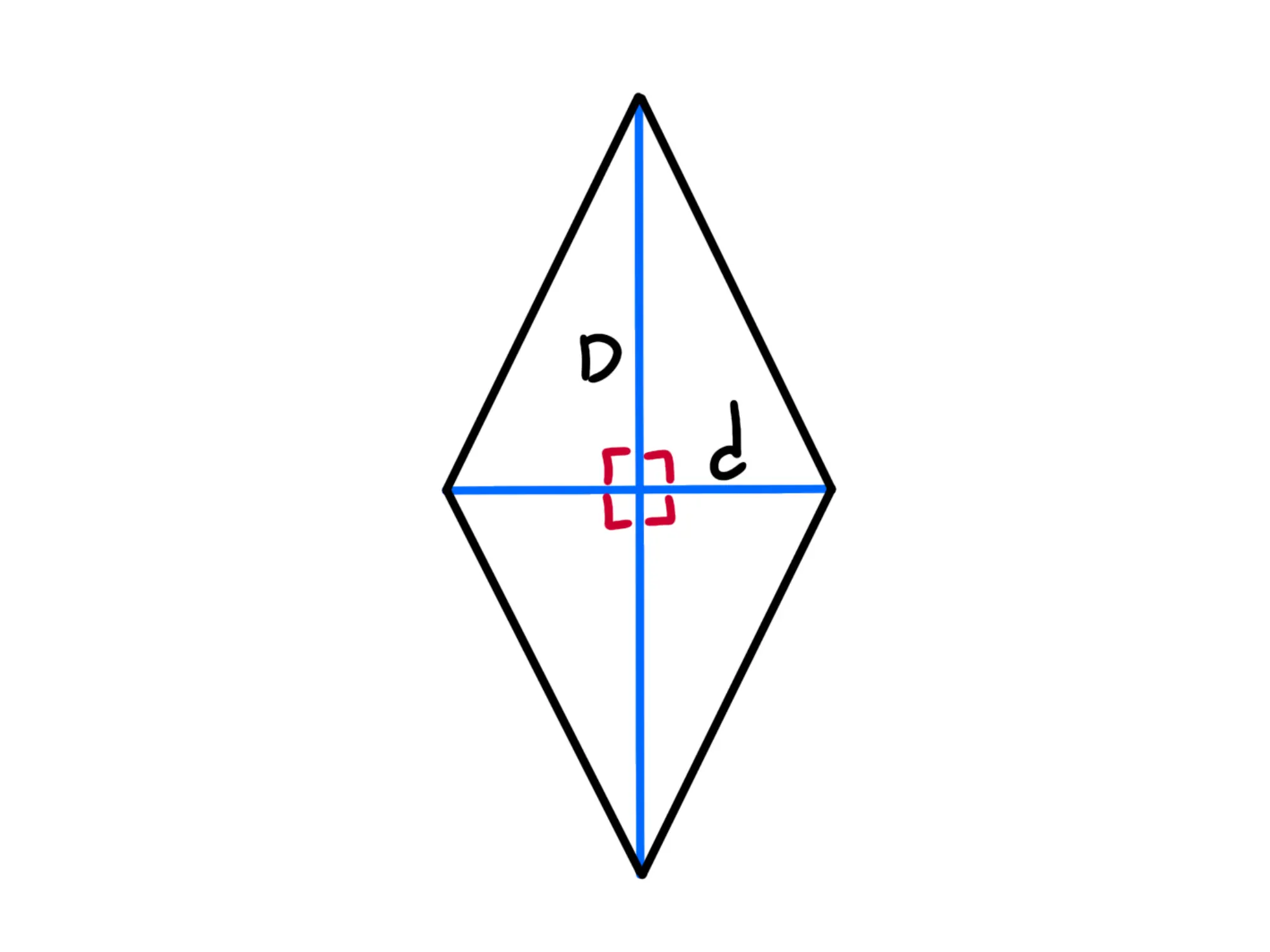
2. Utilizzando le Diagonali
Un'altra formula per calcolare l'area del rombo si basa sulle sue diagonali. Se chiamiamo le diagonali d1 e d2, l'area è data da:
Area = (d1 × d2) / 2
Conoscendo l'area calcolata dalle diagonali e la lunghezza di un lato (l), possiamo calcolare l'altezza usando la formula:
h = Area / l = ((d1 × d2) / 2) / l
Esempio: Se le diagonali di un rombo sono 8 cm e 6 cm, e un lato è 5 cm, l'area è (8 cm × 6 cm) / 2 = 24 cm². Quindi l'altezza è 24 cm² / 5 cm = 4.8 cm.
3. Utilizzando la Trigonometria
Se conosciamo un angolo del rombo (θ) e la lunghezza di un lato (l), possiamo utilizzare la trigonometria per calcolare l'altezza. L'altezza è il lato opposto all'angolo in un triangolo rettangolo formato dall'altezza stessa, dal lato e da una parte della base. Pertanto, possiamo usare la funzione seno:
sin(θ) = altezza / lato
Quindi:
altezza = lato × sin(θ)
Esempio: Se un lato del rombo è 10 cm e un angolo è 30 gradi, l'altezza sarà 10 cm × sin(30°) = 10 cm × 0.5 = 5 cm.
4. Utilizzando il Teorema di Pitagora (Metodo indiretto)
A volte, potremmo conoscere la lunghezza di una diagonale e di un lato. In questo caso, possiamo usare il teorema di Pitagora per trovare una relazione che ci permetta di calcolare l'altezza, sebbene questo metodo sia più indiretto. Poiché le diagonali si bisecano perpendicolarmente, possiamo formare un triangolo rettangolo. Questo metodo richiede passaggi aggiuntivi e potrebbe non essere il più efficiente, ma può essere utile in determinate situazioni.
Esempi Pratici e Applicazioni Reali
La comprensione dell'altezza di un rombo non è solo un esercizio teorico. Ha applicazioni pratiche in diversi campi.
Architettura e Design
Gli architetti e i designer utilizzano le proprietà dei rombi e il calcolo della sua altezza per progettare pavimenti, finestre, e strutture decorative. Ad esempio, un pavimento piastrellato con piastrelle a forma di rombo richiede un'accurata calcolazione delle dimensioni, inclusa l'altezza, per garantire una posa corretta e un aspetto estetico gradevole.
Ingegneria
In ingegneria, i rombi possono essere utilizzati in strutture come ponti o telai. La capacità di calcolare l'altezza e altre dimensioni critiche è essenziale per garantire la stabilità e la resistenza della struttura.
Gioielleria e Artigianato
I rombi sono spesso utilizzati nella gioielleria e nell'artigianato per creare design unici. La precisione nel taglio e nell'assemblaggio di materiali a forma di rombo richiede una conoscenza approfondita delle sue proprietà geometriche, inclusa l'altezza.
Visualizzazione di Dati
In ambito di visualizzazione dati, i rombi (o forme romboidali) possono essere usati per rappresentare determinate categorie o valori in grafici e infografiche. Comprendere le dimensioni e le proporzioni di queste forme è utile per una corretta interpretazione visiva dei dati.
Considerazioni Importanti
Quando si calcola l'altezza di un rombo, è cruciale prestare attenzione alle unità di misura. Assicurarsi che tutte le misure siano espresse nella stessa unità (ad esempio, centimetri, metri, pollici) per evitare errori nei calcoli. Inoltre, è importante scegliere il metodo più appropriato in base alle informazioni disponibili. Se si conoscono l'area e la lunghezza del lato, il primo metodo è il più semplice. Se si conoscono le diagonali, il secondo metodo è più conveniente. Se si conosce un angolo e la lunghezza del lato, la trigonometria è la scelta migliore.
Infine, verificare sempre i risultati ottenuti, utilizzando un calcolatore o un software di geometria per confermare la correttezza dei calcoli.
Riepilogo e Conclusione
Abbiamo esplorato diversi metodi per calcolare l'altezza di un rombo, ognuno dei quali si basa su diverse proprietà geometriche e informazioni disponibili. Ricapitolando, l'altezza può essere calcolata utilizzando l'area e la lunghezza del lato, le diagonali, la trigonometria, o indirettamente attraverso il teorema di Pitagora.
La comprensione di questi metodi non solo fornisce una solida base teorica, ma offre anche strumenti pratici per risolvere problemi reali in vari settori. Che tu sia uno studente, un architetto, un ingegnere, o semplicemente un appassionato di geometria, la capacità di calcolare l'altezza di un rombo è una competenza preziosa.
Ora che hai una comprensione completa dei metodi per calcolare l'altezza di un rombo, mettiti alla prova con alcuni esercizi pratici! Sperimenta con diverse combinazioni di informazioni (area, diagonali, angoli, lunghezza dei lati) e verifica i tuoi risultati. Più pratichi, più diventerai sicuro e abile nel risolvere problemi di geometria. Condividi le tue scoperte e conoscenze con altri, aiutandoli a comprendere e apprezzare la bellezza e l'utilità della geometria.