Qual è L Area Del Quadrato

Avete mai guardato una piastrella, un fazzoletto o una scacchiera e pensato a quanta superficie occupano? Il concetto di area è fondamentale nella nostra vita quotidiana, dall'arredamento di casa alla pianificazione di un giardino. In questo articolo, esploreremo a fondo l'area di una figura geometrica molto semplice ma importantissima: il quadrato. Ci rivolgeremo a studenti, appassionati di geometria, e a chiunque voglia rispolverare le proprie conoscenze matematiche in modo chiaro e accessibile.
Che cos'è un Quadrato?
Prima di calcolare l'area, definiamo cos'è esattamente un quadrato. Un quadrato è un poligono con le seguenti caratteristiche:
- Quattro lati.
- Tutti i lati sono della stessa lunghezza.
- Quattro angoli retti (90 gradi).
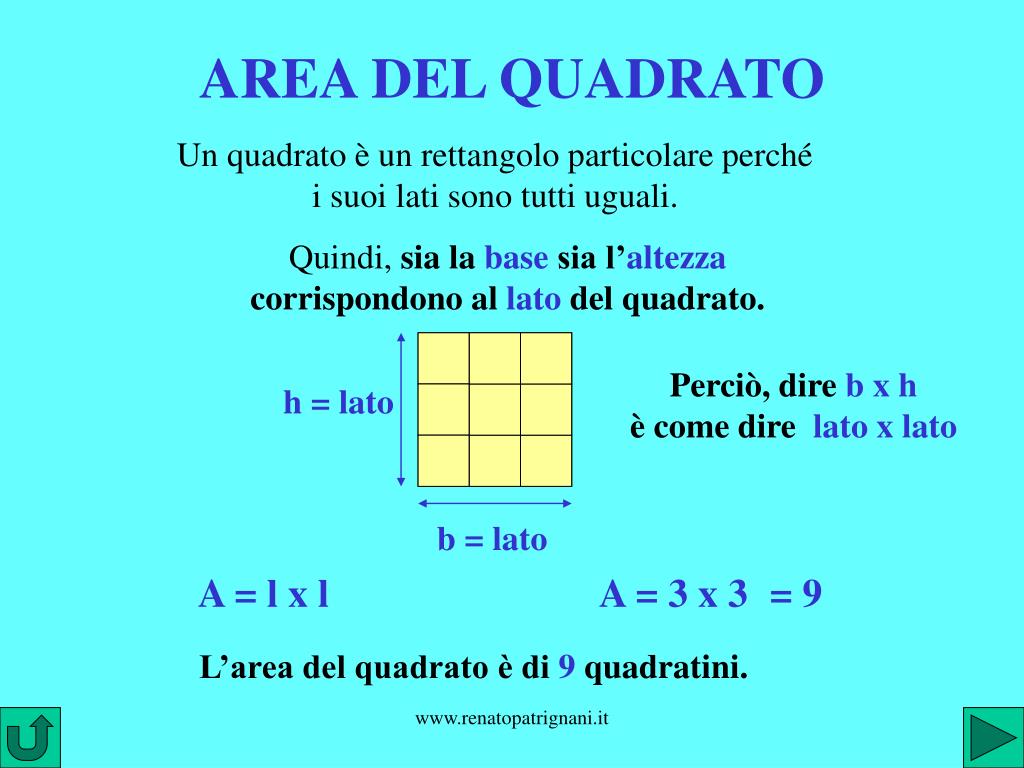
In altre parole, un quadrato è un rettangolo con tutti i lati uguali. Questa proprietà di avere lati uguali è cruciale per il calcolo della sua area.
Area del Quadrato: La Formula Chiave
L'area di una figura geometrica è la misura della superficie che essa occupa. Per il quadrato, il calcolo è particolarmente semplice. La formula per trovare l'area di un quadrato è:
Area = lato × lato
Oppure, in forma più concisa:
Area = l2
Dove 'l' rappresenta la lunghezza di un lato del quadrato. Questa formula deriva direttamente dalla definizione di area come prodotto delle due dimensioni di una figura bidimensionale. Nel caso del quadrato, le due dimensioni sono uguali (i lati).
Esempio Pratico
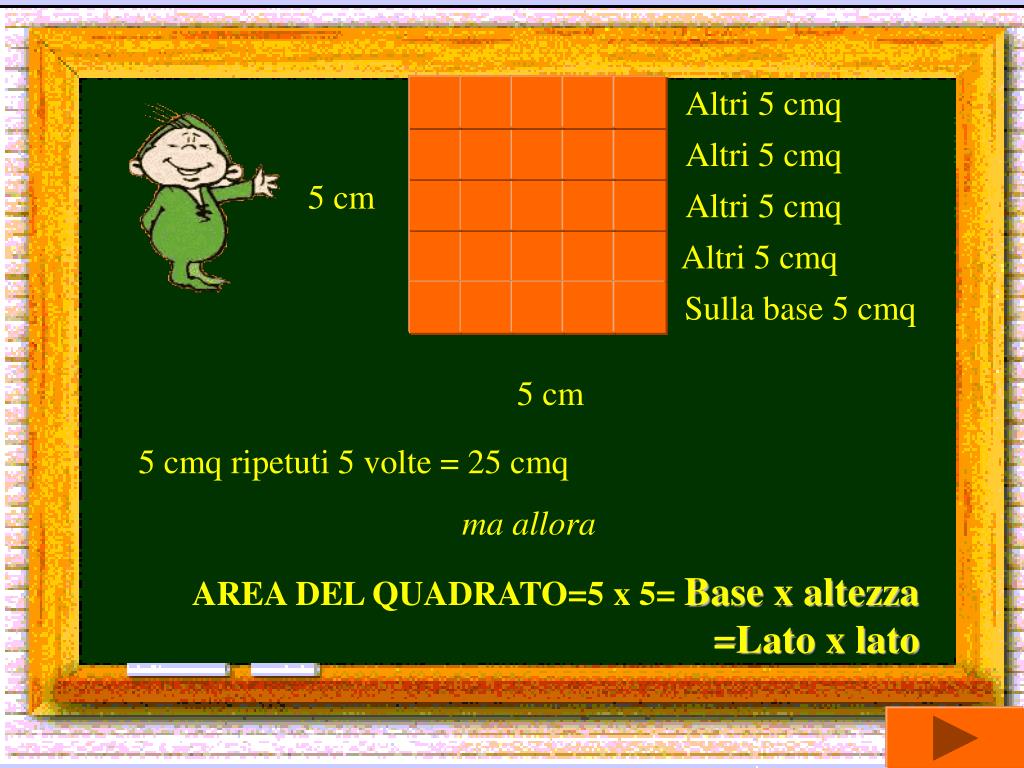
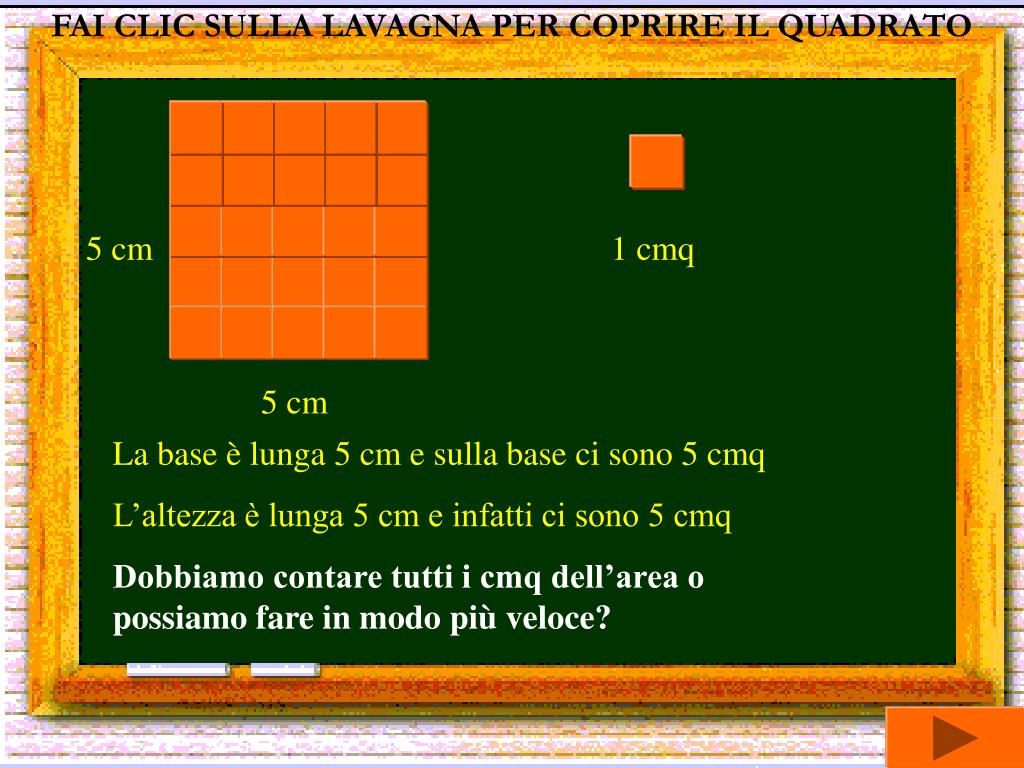
Immaginiamo di avere un quadrato con un lato di 5 centimetri. Per trovare la sua area, applichiamo la formula:
Area = 5 cm × 5 cm = 25 cm2
Quindi, l'area di questo quadrato è di 25 centimetri quadrati. Ricordatevi sempre di esprimere l'area in unità di misura al quadrato, come cm2, m2, ecc.
Come Ricavare il Lato dall'Area
A volte, potremmo trovarci nella situazione opposta: conosciamo l'area di un quadrato e vogliamo trovare la lunghezza del suo lato. In questo caso, dobbiamo fare l'operazione inversa dell'elevazione al quadrato, ovvero calcolare la radice quadrata.
Se Area = l2, allora l = √Area
Esempio Inverso
Supponiamo di sapere che l'area di un quadrato è di 64 metri quadrati. Per trovare la lunghezza del suo lato, calcoliamo la radice quadrata di 64:
l = √64 m2 = 8 m
Quindi, il lato del quadrato è di 8 metri.
Perché è Importante Conoscere l'Area del Quadrato?
La conoscenza dell'area del quadrato non è solo un esercizio matematico astratto. Ha applicazioni pratiche in molti campi:
- Costruzioni: Calcolare la quantità di piastrelle necessarie per pavimentare una stanza quadrata.
- Giardinaggio: Determinare la quantità di erba sintetica necessaria per coprire un'area quadrata.
- Arte e Design: Creare composizioni equilibrate utilizzando forme quadrate.
- Informatica: Calcolare lo spazio occupato da elementi grafici quadrati in un'interfaccia utente.
- Vita Quotidiana: Stimare la quantità di tessuto necessaria per realizzare un fazzoletto quadrato.
Questi sono solo alcuni esempi, ma la capacità di calcolare l'area del quadrato è uno strumento utile in una vasta gamma di situazioni.
Esercizi Pratici per Affinare le Tue Abilità
Per consolidare la tua comprensione, ecco alcuni esercizi pratici. Prova a risolverli da solo, applicando le formule che abbiamo visto:
- Un quadrato ha un lato di 12 cm. Qual è la sua area?
- L'area di un quadrato è di 81 m2. Quanto misura il suo lato?
- Devi pavimentare una stanza quadrata di 4 metri di lato con piastrelle quadrate di 20 cm di lato. Quante piastrelle ti servono? (Suggerimento: converti tutte le misure nella stessa unità)
- Un giardino quadrato ha un'area di 100 m2. Vuoi recintarlo. Quanti metri di recinzione ti servono?
Errori Comuni da Evitare
Anche se la formula per l'area del quadrato è semplice, è facile commettere errori. Ecco alcuni dei più comuni:
- Confondere perimetro e area: Il perimetro è la somma dei lati, mentre l'area è la superficie.
- Dimenticare le unità di misura: L'area deve essere espressa in unità di misura al quadrato.
- Non convertire le unità di misura: Se hai lati in metri e centimetri, devi convertirli nella stessa unità prima di calcolare l'area.
- Applicare la formula sbagliata: Assicurati di usare la formula corretta per l'area del quadrato (l2).
Il Quadrato e Altre Figure Geometriche
La conoscenza dell'area del quadrato è un punto di partenza importante per comprendere l'area di figure geometriche più complesse. Ad esempio:
- Rettangolo: L'area del rettangolo (base × altezza) è strettamente legata all'area del quadrato.
- Rombo: L'area del rombo può essere calcolata conoscendo le sue diagonali, ma il quadrato è un caso speciale di rombo.
- Poligoni Regolari: L'area di molti poligoni regolari può essere approssimata suddividendoli in triangoli o quadrati.
Conclusione: Un Mattoncino Fondamentale
L'area del quadrato è un concetto fondamentale in geometria e ha applicazioni pratiche in molti aspetti della nostra vita. Abbiamo visto la formula chiave, come ricavare il lato dall'area, esempi pratici e gli errori più comuni da evitare. Speriamo che questo articolo ti abbia fornito una comprensione chiara e completa di questo argomento. Ricorda, la geometria è ovunque intorno a noi: osservare il mondo con occhi matematici può arricchire la nostra percezione e la nostra capacità di risolvere problemi. La prossima volta che vedrai un quadrato, saprai esattamente come calcolare la sua area! Continua ad esplorare il mondo della matematica, un passo alla volta.