Qual è L Altezza Del Rombo

L'altezza di un rombo è un concetto geometrico fondamentale che, pur essendo apparentemente semplice, nasconde implicazioni importanti per il calcolo dell'area e per la comprensione delle proprietà di questa figura. Molti si concentrano sui lati e sulle diagonali, ma l'altezza offre un'ulteriore prospettiva per analizzare il rombo. In questo articolo, esploreremo in dettaglio cos'è l'altezza di un rombo, come si calcola e perché è così importante.

Definizione e Proprietà dell'Altezza del Rombo

Cos'è l'Altezza di un Rombo?

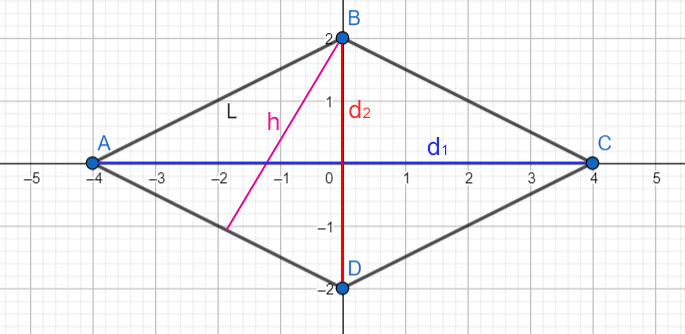
L'altezza di un rombo è la distanza perpendicolare tra due lati paralleli opposti. Essendo un parallelogramma, il rombo ha due coppie di lati paralleli, quindi ha anche due altezze, una relativa a ciascuna coppia di lati paralleli. Tuttavia, dato che tutti i lati del rombo sono congruenti (hanno la stessa lunghezza), le due altezze avranno la stessa misura. Questa è una caratteristica importante da ricordare.

Differenza tra Altezza e Diagonali

È cruciale distinguere tra l'altezza e le diagonali del rombo. Le diagonali sono segmenti che congiungono i vertici opposti e si intersecano perpendicolarmente nel loro punto medio. L'altezza, invece, è un segmento perpendicolare che collega due lati paralleli. Le diagonali sono essenziali per calcolare l'area del rombo usando la formula (d1 * d2) / 2, mentre l'altezza è fondamentale quando si usa la formula base per altezza (b * h).

Relazione tra Altezza, Lati e Angoli

L'altezza di un rombo è strettamente legata alla lunghezza dei suoi lati e all'ampiezza dei suoi angoli interni. Utilizzando la trigonometria, possiamo esprimere l'altezza in funzione del lato e di uno degli angoli acuti o ottusi del rombo. Questa relazione è particolarmente utile quando non si conosce direttamente l'altezza, ma si hanno informazioni sugli angoli e sulla lunghezza dei lati.

Come Calcolare l'Altezza del Rombo

Metodo 1: Conoscendo l'Area e il Lato

Se si conosce l'area (A) del rombo e la lunghezza del suo lato (l), si può calcolare l'altezza (h) utilizzando la formula derivata dall'area del parallelogramma:

A = l * h

Da cui si ricava:

h = A / l

Questo metodo è il più diretto se si hanno già a disposizione l'area e la lunghezza del lato.

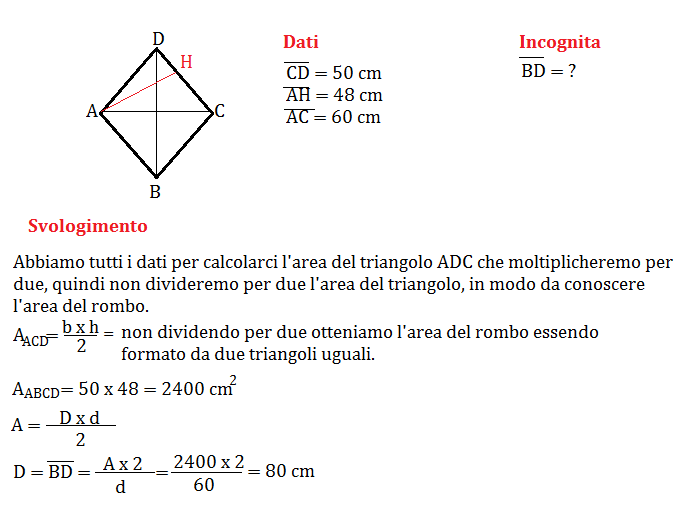
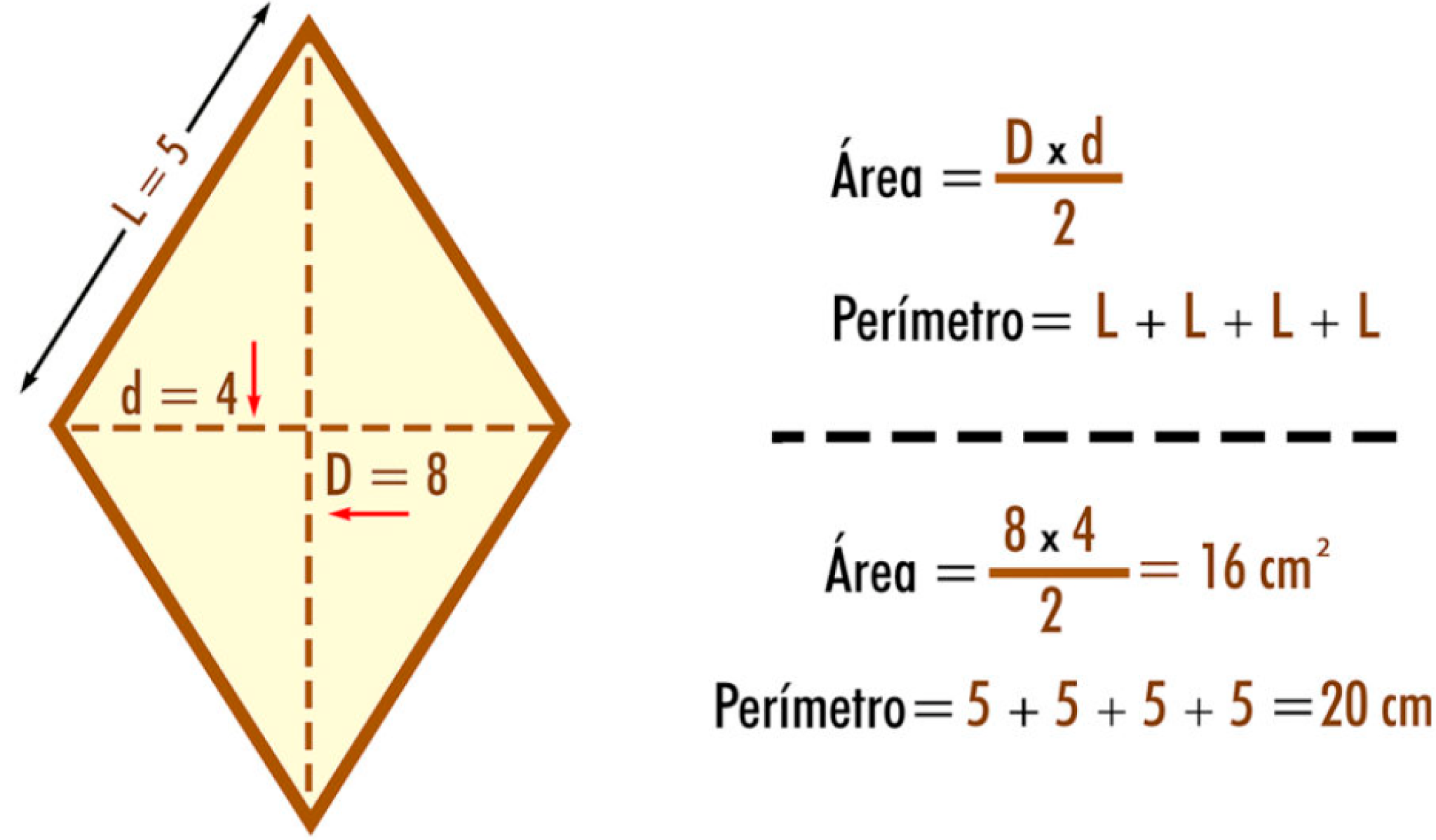
Metodo 2: Conoscendo le Diagonali

Se si conoscono le lunghezze delle diagonali (d1 e d2), è possibile calcolare l'area del rombo come: A = (d1 * d2) / 2. Successivamente, conoscendo l'area e la lunghezza del lato, si può utilizzare il Metodo 1 per trovare l'altezza.

Per calcolare la lunghezza del lato (l) conoscendo le diagonali, si può utilizzare il teorema di Pitagora applicato ai triangoli rettangoli formati dalle diagonali che si intersecano:

l = √((d1/2)² + (d2/2)²)

Quindi, si calcola l'area come detto prima, e poi si applica la formula: h = A / l.

Metodo 3: Utilizzando la Trigonometria

Se si conosce la lunghezza del lato (l) e uno degli angoli interni del rombo (α, ad esempio, un angolo acuto), si può utilizzare la trigonometria per calcolare l'altezza (h). L'altezza è il cateto opposto all'angolo α nel triangolo rettangolo formato dall'altezza, dal lato e da una parte della diagonale. Pertanto:

h = l * sin(α)

È importante assicurarsi che l'angolo α sia espresso in radianti se si utilizza una calcolatrice che lavora in radianti, o in gradi se la calcolatrice lavora in gradi. Se si conosce l'angolo ottuso (β), si può utilizzare la relazione sin(β) = sin(180° - β) = sin(α), quindi il calcolo rimane lo stesso.

Esempi Pratici e Applicazioni Reali

Esempio 1: Calcolo dell'Altezza da Area e Lato

Supponiamo di avere un rombo con area A = 48 cm² e lato l = 8 cm. Per trovare l'altezza, utilizziamo la formula:

h = A / l = 48 cm² / 8 cm = 6 cm

Quindi, l'altezza del rombo è di 6 cm.

Esempio 2: Calcolo dell'Altezza dalle Diagonali

Consideriamo un rombo con diagonali d1 = 12 cm e d2 = 16 cm. Prima calcoliamo l'area:

A = (d1 * d2) / 2 = (12 cm * 16 cm) / 2 = 96 cm²

Poi calcoliamo la lunghezza del lato:

l = √((d1/2)² + (d2/2)²) = √((6 cm)² + (8 cm)²) = √(36 cm² + 64 cm²) = √100 cm² = 10 cm

Infine, calcoliamo l'altezza:

h = A / l = 96 cm² / 10 cm = 9.6 cm

Quindi, l'altezza del rombo è di 9.6 cm.

Esempio 3: Applicazione nel Design e nell'Architettura

I rombi sono spesso utilizzati in design e in architettura, ad esempio, per la pavimentazione di superfici o per la creazione di motivi decorativi. Conoscere l'altezza di un rombo è essenziale per calcolare la quantità di materiale necessario per coprire una determinata area o per assicurarsi che i motivi siano proporzionati e esteticamente gradevoli. Immaginate di dover posare delle piastrelle a forma di rombo in un bagno. Conoscere l'altezza vi permetterà di calcolare precisamente quanti metri lineari di stucco vi serviranno per le fughe. Oppure pensate ad una struttura a forma di rombo in un ponte. In questo caso, la conoscenza dell'altezza è fondamentale per calcolare le forze che agiscono sulla struttura.

Esempio 4: Applicazione nell'Ingegneria

Nell'ingegneria, il calcolo dell'altezza del rombo può essere utile per l'analisi di strutture che incorporano elementi romboidali, come ad esempio tralicci o componenti di macchinari. La precisione nel calcolo delle dimensioni e delle proprietà geometriche è fondamentale per garantire la stabilità e la sicurezza delle strutture.

Conclusioni

L'altezza del rombo è un parametro geometrico cruciale che permette di calcolare l'area e di analizzare le proprietà di questa figura. Abbiamo esplorato diversi metodi per calcolare l'altezza, a seconda delle informazioni disponibili (area, lato, diagonali, angoli). La comprensione di questi metodi è fondamentale per risolvere problemi di geometria e per applicazioni pratiche in vari campi, dal design all'ingegneria. Sperimentate con i diversi metodi presentati e cercate di applicarli a problemi concreti per consolidare la vostra comprensione del concetto di altezza del rombo. Ricordate che la geometria, come la matematica in generale, si impara attraverso la pratica e l'applicazione dei concetti.

Ora che avete una solida comprensione di come calcolare l'altezza di un rombo, sfidatevi con esercizi più complessi. Considerate rombi con angoli particolari (ad esempio, rombi che sono anche quadrati) e verificate come le formule si semplificano in questi casi. Condividete le vostre scoperte e i vostri dubbi con altri appassionati di geometria per approfondire ulteriormente la vostra conoscenza.