Quadrati Perfetti Da 1 A 100

Quante volte ti sei trovato di fronte a un numero e ti sei chiesto se fosse un quadrato perfetto? Magari in un problema di matematica, durante un gioco di logica, o persino mentre organizzavi delle piastrelle? Capire i quadrati perfetti, soprattutto quelli da 1 a 100, può semplificarti la vita più di quanto immagini. Non si tratta solo di matematica astratta, ma di uno strumento pratico per risolvere problemi reali.

Questo articolo è pensato per te, che magari hai dimenticato le basi, o che vuoi semplicemente rinfrescare le tue conoscenze. Ti guideremo attraverso i quadrati perfetti da 1 a 100, spiegandoti cosa sono, come identificarli, e perché sono importanti. Cercheremo di rendere tutto il più semplice e chiaro possibile, evitando tecnicismi inutili e concentrandoci sull'applicazione pratica.

Cosa Sono i Quadrati Perfetti?

Un quadrato perfetto è un numero intero che può essere ottenuto elevando al quadrato un altro numero intero. In altre parole, è il risultato della moltiplicazione di un numero per se stesso. Ad esempio, 9 è un quadrato perfetto perché è uguale a 3 x 3 (o 3²). Il concetto fondamentale è che la radice quadrata di un quadrato perfetto è un numero intero.

Pensala così: immagina di voler formare un quadrato perfetto con delle tessere. Se hai 9 tessere, puoi disporle in un quadrato 3x3. Se hai 10 tessere, non puoi formare un quadrato perfetto; ti avanzerebbe una tessera.

Un altro esempio concreto? Pensa a un campo di grano. Se hai un campo che è esattamente un quadrato perfetto, puoi dividerlo in quadrati più piccoli senza avere scarti. Se il campo non è un quadrato perfetto, avrai sempre uno scarto di terreno che non può essere facilmente suddiviso.

I Quadrati Perfetti da 1 a 100

Ecco la lista completa dei quadrati perfetti da 1 a 100:

• 1 (1 x 1 = 1²)
• 4 (2 x 2 = 2²)
• 9 (3 x 3 = 3²)
• 16 (4 x 4 = 4²)
• 25 (5 x 5 = 5²)
• 36 (6 x 6 = 6²)
• 49 (7 x 7 = 7²)
• 64 (8 x 8 = 8²)
• 81 (9 x 9 = 9²)
• 100 (10 x 10 = 10²)

Memorizzare questa lista può essere estremamente utile per risolvere problemi rapidamente. Non devi per forza impararla a memoria, ma familiarizzare con questi numeri ti farà risparmiare tempo ed energia.

Come Riconoscere un Quadrato Perfetto

Ci sono diversi metodi per riconoscere un quadrato perfetto. Eccone alcuni:

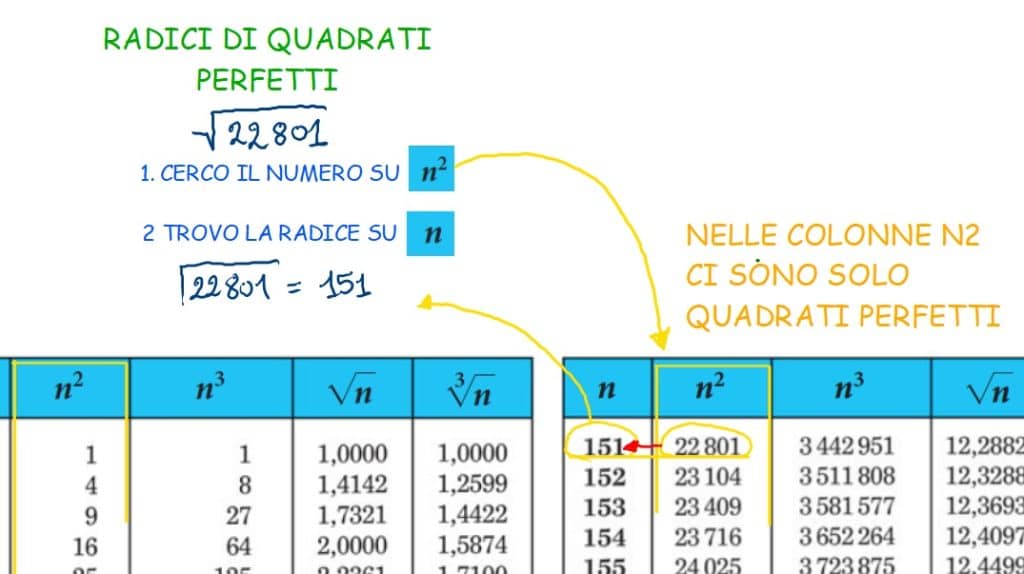
• Radice Quadrata: Calcola la radice quadrata del numero. Se il risultato è un numero intero, allora il numero è un quadrato perfetto. La calcolatrice è tua amica in questo caso.
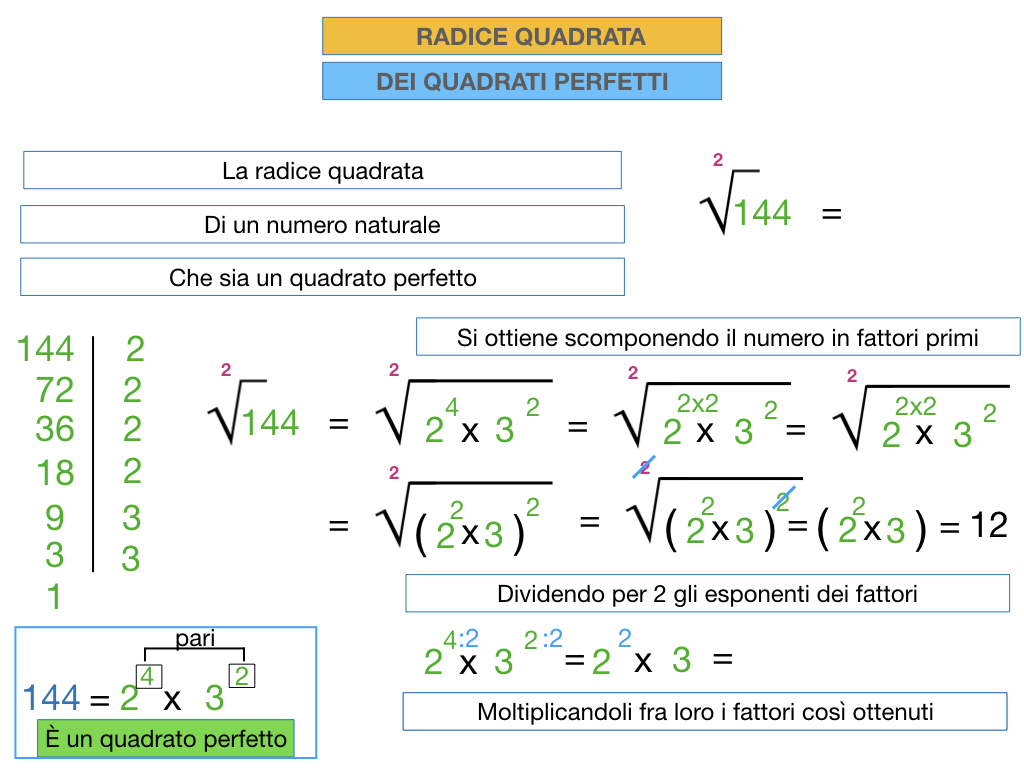
• Scomposizione in Fattori Primi: Scomponi il numero in fattori primi. Se ogni fattore primo compare un numero pari di volte, allora il numero è un quadrato perfetto. Ad esempio, 36 = 2 x 2 x 3 x 3 = 2² x 3². Ogni fattore (2 e 3) compare due volte, quindi 36 è un quadrato perfetto.
• Pattern dei Numeri: Osserva i numeri. I quadrati perfetti tendono ad avere pattern numerici riconoscibili. Ad esempio, la differenza tra due quadrati perfetti consecutivi aumenta sempre di due. (4-1=3, 9-4=5, 16-9=7, ecc.)
• Stima Approssimativa: Se non hai una calcolatrice a portata di mano, prova a stimare la radice quadrata. Ad esempio, sai che 5² è 25 e 6² è 36. Quindi, qualsiasi numero tra 25 e 36 non sarà un quadrato perfetto.

Perché i Quadrati Perfetti Sono Importanti?

I quadrati perfetti non sono solo un concetto matematico astratto. Hanno applicazioni pratiche in diverse aree:

• Geometria: Calcolo delle aree di quadrati e delle lunghezze dei lati. Se sai che l'area di un quadrato è 64, sai automaticamente che il lato è 8.
• Algebra: Semplificazione di espressioni algebriche e risoluzione di equazioni. Molte equazioni quadratiche possono essere risolte facilmente se riconosci i quadrati perfetti.
• Informatica: Ottimizzazione di algoritmi e gestione della memoria. Alcuni algoritmi di ordinamento e ricerca sono più efficienti quando i dati sono organizzati in strutture che coinvolgono quadrati perfetti.
• Architettura e Design: Progettazione di spazi e strutture che siano esteticamente piacevoli e funzionali. Le proporzioni basate sui quadrati perfetti spesso risultano armoniose all'occhio umano.
• Giochi e Puzzle: Risoluzione di enigmi logici e giochi di strategia. Molti giochi utilizzano griglie quadrate, e la conoscenza dei quadrati perfetti può darti un vantaggio.

Immagina di dover calcolare la quantità di materiale necessario per costruire una piattaforma quadrata. Se conosci l'area della piattaforma, trovare la lunghezza del lato diventa un gioco da ragazzi se riconosci i quadrati perfetti. Oppure, pensa di dover dividere un terreno in parcelle quadrate uguali. La conoscenza dei quadrati perfetti ti aiuta a determinare se è possibile farlo senza sprechi.

Contro-Argomentazioni: È Davvero Utile Saperli a Memoria?

Alcuni potrebbero obiettare che, nell'era delle calcolatrici e dei computer, imparare a memoria i quadrati perfetti è un esercizio inutile. Si potrebbe argomentare che è sufficiente sapere come usare uno strumento per calcolare la radice quadrata.

Tuttavia, ci sono diverse ragioni per cui avere una buona conoscenza dei quadrati perfetti è ancora vantaggioso:

• Velocità: Conoscere i quadrati perfetti ti permette di risolvere problemi rapidamente, senza dover sempre ricorrere a una calcolatrice. Questo è particolarmente utile in situazioni in cui il tempo è un fattore critico.
• Comprensione: Familiarizzare con i quadrati perfetti ti aiuta a sviluppare una comprensione più profonda dei concetti matematici sottostanti. Non si tratta solo di ottenere una risposta, ma di capire perché quella risposta è corretta.
• Intuito: Avere una solida base di conoscenze matematiche ti permette di sviluppare un intuito che ti aiuta a risolvere problemi complessi in modo più efficiente.
• Problem Solving: In situazioni in cui non hai accesso a una calcolatrice, la tua conoscenza dei quadrati perfetti può fare la differenza tra risolvere un problema e arrenderti.

Inoltre, la conoscenza dei quadrati perfetti è un ottimo punto di partenza per esplorare concetti matematici più avanzati, come i numeri irrazionali e le radici quadrate non perfette.

Un Approccio Soluzione-Focalizzato

Invece di concentrarti solo sui problemi che possono sorgere dalla mancanza di conoscenza dei quadrati perfetti, cerchiamo di focalizzarci sulle soluzioni. Ecco alcuni suggerimenti per migliorare la tua comprensione e memorizzazione:

• Pratica: Risolvi esercizi e problemi che coinvolgono i quadrati perfetti. Più ti eserciti, più diventeranno familiari.
• Flashcard: Crea flashcard con i numeri da 1 a 100 e scrivi la loro radice quadrata sul retro. Usa le flashcard per esercitarti regolarmente.
• Giochi: Esistono molti giochi online e app che possono aiutarti a imparare i quadrati perfetti in modo divertente e interattivo.
• Visualizzazione: Cerca di visualizzare i quadrati perfetti come figure geometriche. Immagina di disporre le tessere in un quadrato perfetto.
• Associazione: Associa i quadrati perfetti a eventi o oggetti familiari. Ad esempio, puoi associare il numero 16 all'età in cui puoi prendere la patente.

Ricorda, l'apprendimento è un processo graduale. Non scoraggiarti se all'inizio fai fatica a memorizzare i quadrati perfetti. Continua a esercitarti e vedrai che con il tempo diventeranno una seconda natura.

Un Esempio Pratico

Immagina di dover calcolare l'area di un quadrato il cui lato è lungo 9 metri. Se sai che 9 è un quadrato perfetto (3²), puoi facilmente calcolare l'area elevando al quadrato la lunghezza del lato: 9² = 81 metri quadrati. Se invece non ricordi che 9 è un quadrato perfetto, potresti dover ricorrere a una calcolatrice o fare il calcolo a mano, perdendo tempo prezioso.

Un altro esempio: stai progettando un giardino quadrato e vuoi che l'area sia di 49 metri quadrati. Quale deve essere la lunghezza del lato? Se riconosci che 49 è un quadrato perfetto (7²), sai immediatamente che il lato deve essere lungo 7 metri.

Conclusione

I quadrati perfetti da 1 a 100 sono un concetto matematico fondamentale con applicazioni pratiche in diverse aree. Sebbene l'uso delle calcolatrici sia diffuso, avere una buona conoscenza dei quadrati perfetti può migliorare la tua velocità, comprensione e intuito nella risoluzione di problemi.

Speriamo che questo articolo ti abbia fornito una panoramica chiara e comprensibile dei quadrati perfetti. Ti invitiamo a mettere in pratica le conoscenze acquisite risolvendo esercizi e problemi. Ricorda, la pratica rende perfetti!

Ora, ti chiediamo: come pensi di applicare questa conoscenza nella tua vita quotidiana? Proverai a individuare i quadrati perfetti che ti circondano?