Punto Medio Di Un Segmento Esercizi Svolti

Hai mai avuto la necessità di trovare esattamente il centro di una linea, che si tratti di dividere equamente un pezzo di stoffa, posizionare un oggetto in modo simmetrico o risolvere un problema di geometria? Il punto medio di un segmento è un concetto fondamentale nella matematica e nella vita di tutti i giorni. Questa guida pratica ti fornirà una comprensione chiara e completa del punto medio, corredata da esercizi svolti passo passo per aiutarti a padroneggiare questa abilità essenziale.

Questo articolo è rivolto a studenti di scuola media e superiore, a chiunque stia ripassando concetti di geometria, o semplicemente a chi è curioso di scoprire come calcolare il punto medio in modo semplice ed efficace. Preparati ad acquisire una solida base teorica e a mettere in pratica le tue conoscenze con esempi concreti!

Cos'è il Punto Medio di un Segmento?

Definiamo innanzitutto cos'è un segmento. Un segmento è una porzione di retta delimitata da due punti, chiamati estremi. Il punto medio, come suggerisce il nome, è il punto che divide il segmento in due parti uguali. In altre parole, la distanza tra un estremo e il punto medio è esattamente la stessa della distanza tra il punto medio e l'altro estremo.

Concetti chiave:

• Un segmento ha due estremi.
• Il punto medio divide il segmento in due parti congruenti (uguali).
• Il punto medio è equidistante dagli estremi del segmento.

Come Calcolare il Punto Medio

Esistono due scenari principali in cui potremmo voler calcolare il punto medio:

1. Segmento su una Retta Numerica

Se il segmento si trova su una retta numerica, dove gli estremi sono rappresentati da numeri, il calcolo è semplicissimo. Basta trovare la media aritmetica delle coordinate degli estremi.

Formula: Se gli estremi del segmento sono rappresentati dai numeri *a* e *b*, allora il punto medio *M* è dato da:

M = (a + b) / 2

Esempio:

Supponiamo che gli estremi del segmento sulla retta numerica siano 3 e 7. Per trovare il punto medio, applichiamo la formula:

M = (3 + 7) / 2 = 10 / 2 = 5

Quindi, il punto medio del segmento è 5.

2. Segmento nel Piano Cartesiano

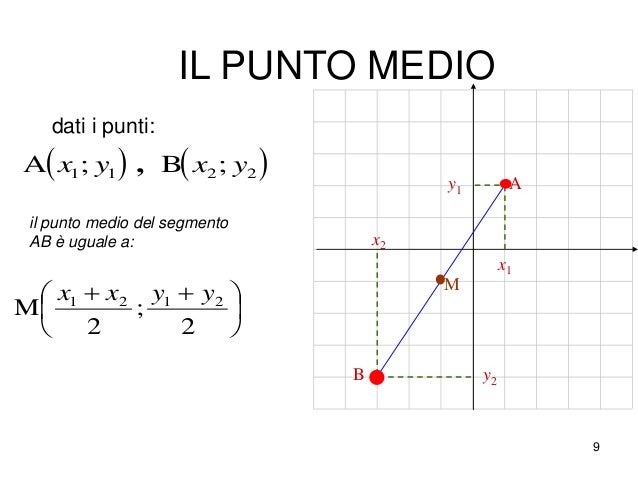
Quando il segmento si trova nel piano cartesiano, gli estremi sono rappresentati da coppie di coordinate (x, y). In questo caso, dobbiamo calcolare la media aritmetica delle coordinate x e delle coordinate y separatamente.

Formula: Se gli estremi del segmento sono A(x₁, y₁) e B(x₂, y₂), allora il punto medio M(xₘ, yₘ) è dato da:

xₘ = (x₁ + x₂) / 2

yₘ = (y₁ + y₂) / 2

Esempio:

Supponiamo che gli estremi del segmento nel piano cartesiano siano A(2, 4) e B(6, 8). Per trovare il punto medio, applichiamo le formule:

xₘ = (2 + 6) / 2 = 8 / 2 = 4

yₘ = (4 + 8) / 2 = 12 / 2 = 6

Quindi, il punto medio del segmento è M(4, 6).

Esercizi Svolti Passo Passo

Ora mettiamo in pratica le nostre conoscenze con alcuni esercizi svolti. Segui attentamente i passaggi per capire a fondo il procedimento.

Esercizio 1: Retta Numerica

Testo: Trova il punto medio del segmento sulla retta numerica con estremi -2 e 8.

Soluzione:

1. Identifica gli estremi: a = -2, b = 8
2. Applica la formula: M = (a + b) / 2
3. Sostituisci i valori: M = (-2 + 8) / 2
4. Calcola: M = 6 / 2 = 3
5. Risposta: Il punto medio è 3.

Esercizio 2: Piano Cartesiano

Testo: Trova il punto medio del segmento nel piano cartesiano con estremi A(-1, 3) e B(5, -1).

Soluzione:

1. Identifica gli estremi: A(x₁, y₁) = (-1, 3), B(x₂, y₂) = (5, -1)
2. Applica le formule:
   • xₘ = (x₁ + x₂) / 2
   • yₘ = (y₁ + y₂) / 2
3. Sostituisci i valori:
   • xₘ = (-1 + 5) / 2
   • yₘ = (3 + (-1)) / 2
4. Calcola:
   • xₘ = 4 / 2 = 2
   • yₘ = 2 / 2 = 1
5. Risposta: Il punto medio è M(2, 1).

Esercizio 3: Un po' più complesso

Testo: Il punto medio di un segmento è M(3, 2). Uno degli estremi è A(1, 5). Trova le coordinate dell'altro estremo B(x₂, y₂).

Soluzione:

1. Comprendere il problema: Questa volta ci viene dato il punto medio e uno degli estremi, e dobbiamo trovare l'altro estremo.
2. Utilizzare le formule del punto medio: Sappiamo che
   • xₘ = (x₁ + x₂) / 2 e yₘ = (y₁ + y₂) / 2
3. Sostituire i valori conosciuti:
   • 3 = (1 + x₂) / 2 e 2 = (5 + y₂) / 2
4. Risolvere per x₂ e y₂:
   • Moltiplicare entrambi i lati delle equazioni per 2: 6 = 1 + x₂ e 4 = 5 + y₂
   • Sottrarre 1 da entrambi i lati della prima equazione e 5 dalla seconda: 5 = x₂ e -1 = y₂
5. Risposta: L'altro estremo è B(5, -1).

Consigli Utili per Risolvere gli Esercizi

Ecco alcuni consigli pratici per affrontare gli esercizi sul punto medio con successo:

• Disegna un diagramma: Se stai lavorando con il piano cartesiano, disegnare un grafico del segmento e dei punti ti aiuterà a visualizzare il problema e a evitare errori.
• Etichetta chiaramente i punti: Etichettare gli estremi e il punto medio con le loro coordinate ti aiuterà a tenere traccia delle informazioni e a utilizzare correttamente le formule.
• Verifica la tua risposta: Dopo aver calcolato il punto medio, controlla che sia effettivamente a metà strada tra gli estremi. Puoi farlo calcolando la distanza tra il punto medio e ciascun estremo e verificando che siano uguali.
• Non aver paura di chiedere aiuto: Se hai difficoltà a risolvere un esercizio, non esitare a chiedere aiuto al tuo insegnante, a un compagno di classe o a cercare risorse online.

Applicazioni Pratiche del Punto Medio

Il concetto di punto medio non è solo un esercizio teorico. Trova applicazione in diversi campi, tra cui:

• Geometria: Calcolo di aree e perimetri, dimostrazione di teoremi.
• Architettura e Ingegneria: Determinazione del centro di gravità, progettazione di strutture simmetriche.
• Grafica Computerizzata: Creazione di animazioni e modelli 3D.
• Navigazione: Calcolo della posizione intermedia tra due punti.
• Vita quotidiana: Dividere una torta a metà, appendere un quadro in modo simmetrico.

Conclusione

Congratulazioni! Hai completato questa guida pratica sul punto medio di un segmento. Ora hai una solida comprensione del concetto, delle formule e delle applicazioni. Ricorda che la pratica è fondamentale per padroneggiare qualsiasi abilità matematica. Continua a esercitarti con gli esercizi e non esitare a esplorare ulteriori risorse per approfondire le tue conoscenze.

Spero che questa guida ti sia stata utile. Continua a esplorare il meraviglioso mondo della geometria e a scoprire come la matematica può aiutarti a risolvere problemi reali e a comprendere meglio il mondo che ti circonda! Buono studio!