Punto Di Intersezione Delle Altezze Di Un Triangolo

Capita a tutti, a volte, di sentirsi persi. Come un navigatore senza bussola, ci troviamo di fronte a problemi che sembrano insolubili, intricati come un nodo marinaro. In matematica, così come nella vita, spesso la chiave per risolvere un problema complesso risiede nella comprensione dei suoi elementi fondamentali. Oggi, esploreremo un concetto geometrico di base ma incredibilmente potente: il punto di intersezione delle altezze di un triangolo, noto anche come ortocentro. Può sembrare una nozione astratta, relegata ai libri di testo, ma vi assicuro che nasconde una bellezza e un’utilità che vanno ben oltre la pura teoria.
Ma perché dovremmo preoccuparci dell'ortocentro? Non si tratta solo di superare un esame di geometria. Comprendere come le altezze di un triangolo si incontrano in un unico punto ci fornisce una visione profonda delle proprietà dei triangoli stessi, e ci apre la porta a risolvere problemi più complessi in ambiti che vanno dalla fisica all'ingegneria, fino all'arte e all'architettura. Pensate alla stabilità di una struttura, alla progettazione di un ponte, o alla calibrazione di un sistema di coordinate in un software di grafica 3D. In tutti questi casi, la comprensione delle relazioni geometriche fondamentali, come quella che stiamo per esplorare, può fare la differenza tra un progetto ben riuscito e un disastro.
Cos'è un'Altezza? Rinfreschiamo la Memoria
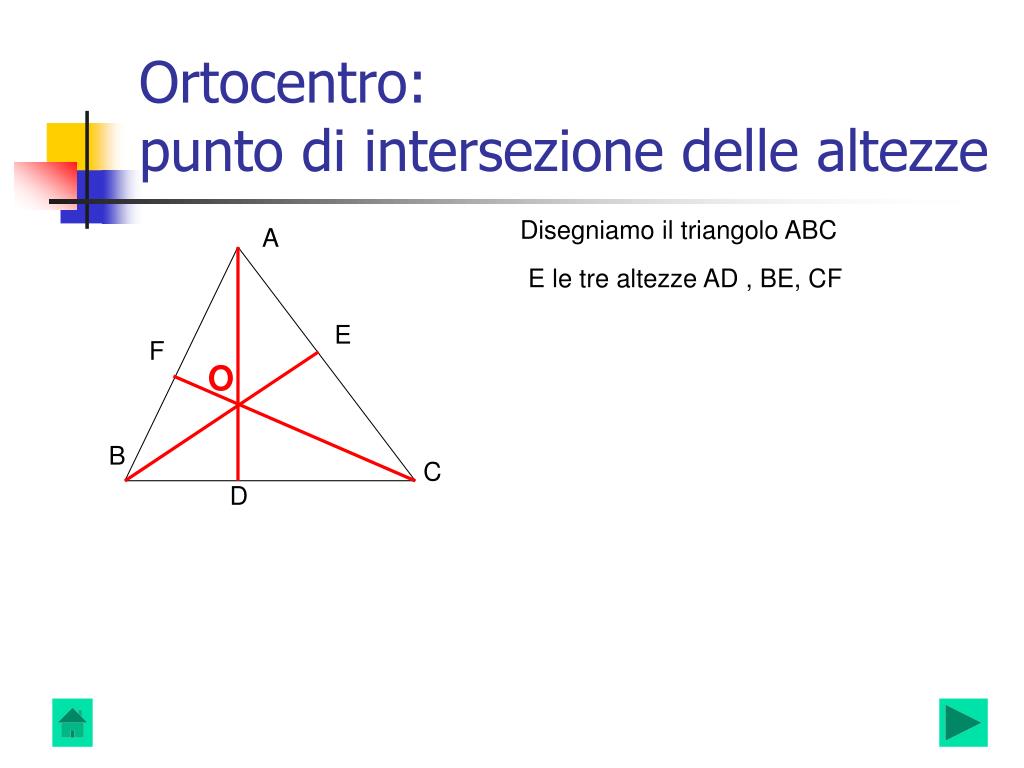
Prima di addentrarci nel punto di intersezione, assicuriamoci di avere ben chiaro cosa intendiamo per altezza di un triangolo. Immaginate di piantare un palo (l'altezza) nel terreno (un lato del triangolo) in modo che sia perfettamente perpendicolare alla superficie. Formalmente, un'altezza di un triangolo è un segmento di retta che parte da un vertice e cade perpendicolarmente sul lato opposto (o sul suo prolungamento). Ogni triangolo ha tre altezze, una per ogni vertice.
- Definizione: Un'altezza è un segmento perpendicolare tracciato da un vertice al lato opposto (o al suo prolungamento).
- Perpendicolarità: L'angolo tra l'altezza e il lato opposto è sempre di 90 gradi.
- Tre Altezze: Ogni triangolo possiede tre altezze, una per ciascun vertice.
L'Ortocentro: Il Punto d'Incontro
Ed ecco il punto cruciale: le tre altezze di un triangolo si intersecano sempre in un unico punto. Questo punto speciale è chiamato ortocentro del triangolo. La sua posizione varia a seconda della forma del triangolo, e questo è uno degli aspetti più interessanti da esplorare.
Dove si Trova l'Ortocentro?
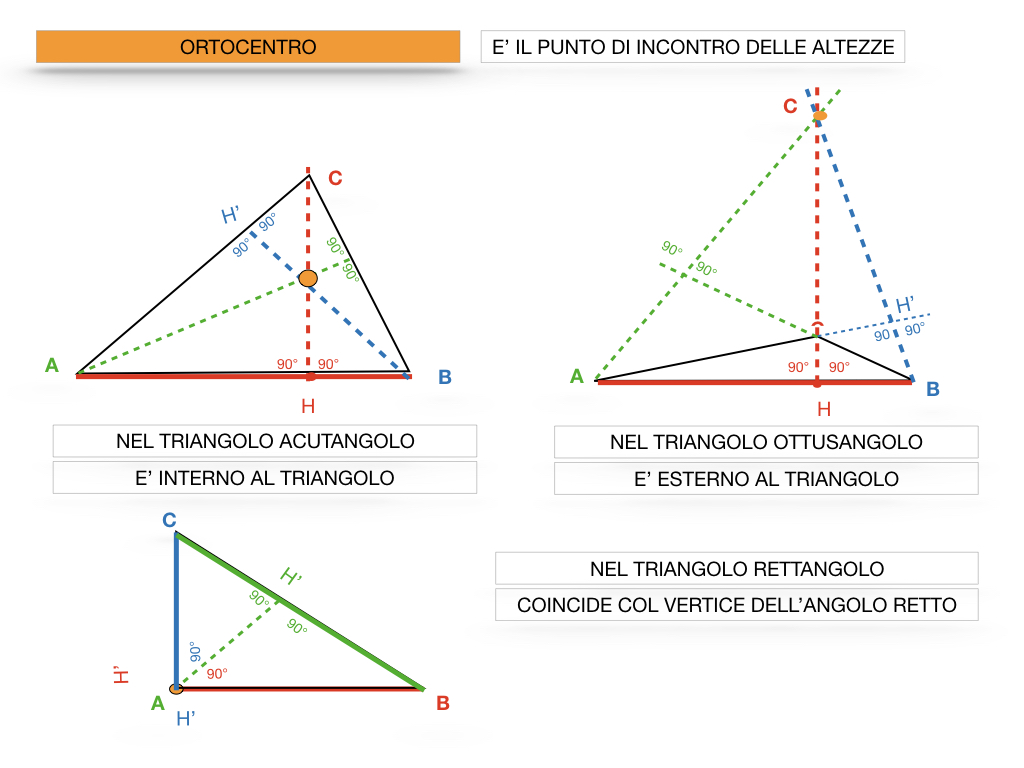
La posizione dell'ortocentro dipende dal tipo di triangolo:
- Triangolo Acutangolo (tutti gli angoli acuti): L'ortocentro si trova all'interno del triangolo.
- Triangolo Rettangolo (un angolo retto): L'ortocentro coincide con il vertice dell'angolo retto. Questo è un caso particolarmente elegante e facile da visualizzare.
- Triangolo Ottusangolo (un angolo ottuso): L'ortocentro si trova all'esterno del triangolo. Questo può sembrare controintuitivo, ma è una conseguenza diretta della necessità di prolungare i lati per tracciare le altezze.
Capire questa variazione è fondamentale. Immaginate di progettare una struttura a triangolo: la posizione dell'ortocentro influenzerà la distribuzione delle forze e quindi la stabilità dell'intera costruzione. Un ingegnere dovrà tenere conto di questa posizione per assicurarsi che la struttura sia in grado di sopportare il peso e le sollecitazioni a cui sarà sottoposta.
Dimostrare l'Esistenza dell'Ortocentro: Un Approccio
L'affermazione che le tre altezze si incontrano sempre in un punto non è semplicemente un'osservazione empirica. È un teorema geometrico che può essere dimostrato rigorosamente. Esistono diverse dimostrazioni, una delle quali si basa sull'utilizzo di triangoli simili e di proprietà delle rette parallele.
Un metodo comune consiste nel costruire un triangolo più grande, circoscritto al triangolo originale, in modo che i lati del triangolo originale siano paralleli ai lati del triangolo più grande. Le altezze del triangolo originale diventano gli assi dei lati del triangolo più grande, e sappiamo che gli assi di un triangolo concorrono in un punto (il circocentro). Questo dimostra che anche le altezze del triangolo originale concorrono in un punto, l'ortocentro.
Contro-Argomentazioni e Chiarimenti
Alcuni potrebbero obiettare che l'ortocentro non è sempre "utile" in senso pratico diretto. È vero, raramente ci troveremo nella vita di tutti i giorni a dover calcolare la posizione precisa dell'ortocentro di un triangolo disegnato sulla sabbia. Tuttavia, il concetto di ortocentro è un esempio perfetto di come la matematica astratta possa fornire strumenti potenti per la risoluzione di problemi concreti, anche se in modo indiretto.
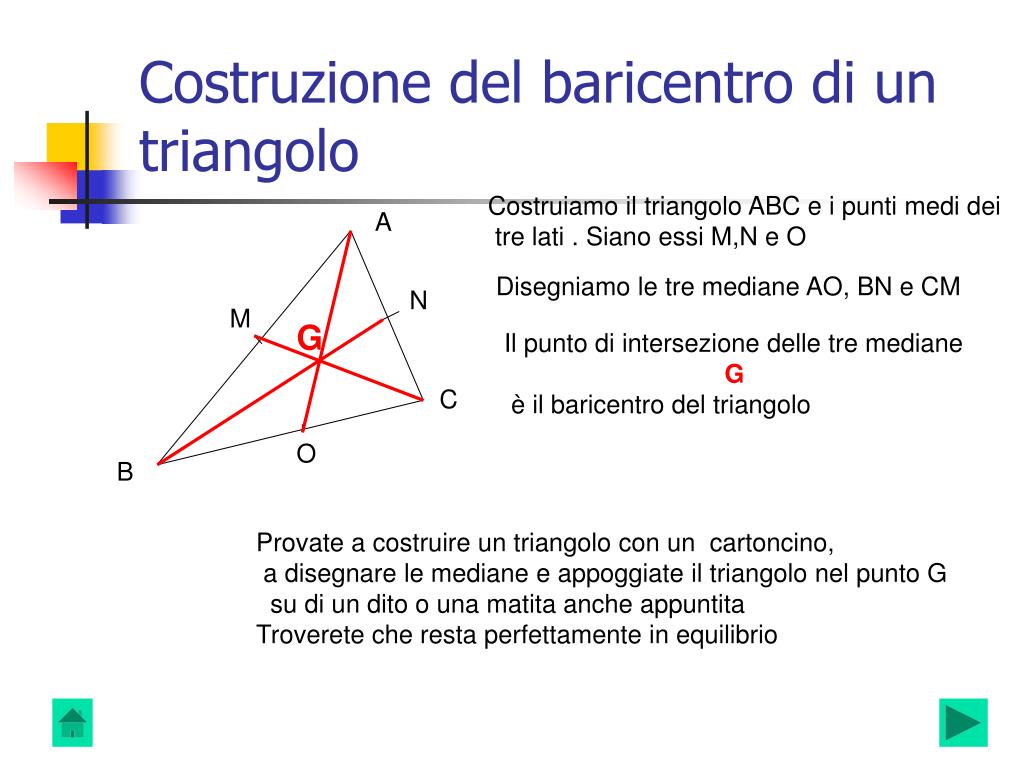
Un altro punto che spesso genera confusione è la distinzione tra ortocentro, baricentro, incentro e circocentro. Sono tutti punti notevoli di un triangolo, ma ognuno ha una definizione e proprietà diverse. Il baricentro è il punto di incontro delle mediane, l'incentro è il punto di incontro delle bisettrici, e il circocentro è il punto di incontro degli assi. È importante non confonderli, poiché ognuno di essi ha un significato geometrico e applicazioni specifiche.
Applicazioni Pratiche (Anche se Nascoste)
Sebbene l'applicazione diretta dell'ortocentro possa non essere immediatamente evidente, la sua comprensione contribuisce a sviluppare un pensiero geometrico più solido. Questo, a sua volta, si rivela utile in diverse discipline:
- Architettura e Ingegneria: La progettazione di strutture stabili richiede una profonda comprensione delle relazioni geometriche e delle forze. La conoscenza dell'ortocentro, e più in generale delle proprietà dei triangoli, contribuisce a questo.
- Grafica Computerizzata e Modellazione 3D: I triangoli sono i mattoni fondamentali della modellazione 3D. Comprendere le loro proprietà geometriche è essenziale per la creazione di modelli accurati e realistici.
- Fisica: Molti problemi di fisica, come quelli relativi alla statica e alla dinamica, coinvolgono la risoluzione di forze che possono essere rappresentate vettorialmente. La geometria dei triangoli è uno strumento fondamentale per analizzare queste forze.
Un Esempio Concreto: Strutture a Traliccio
Consideriamo una struttura a traliccio, come un ponte o una gru. Queste strutture sono composte da una rete di triangoli interconnessi. La stabilità di una struttura a traliccio dipende dalla distribuzione delle forze all'interno dei triangoli. Comprendere le proprietà dei triangoli, inclusa la posizione dell'ortocentro (anche se non esplicitamente calcolato), aiuta gli ingegneri a progettare strutture che siano in grado di sopportare il peso e le sollecitazioni in modo efficiente.
Un Pensiero Finale: La Bellezza della Geometria
L'esplorazione del punto di intersezione delle altezze di un triangolo ci ha permesso di apprezzare la bellezza e l'eleganza della geometria. Abbiamo visto come un concetto apparentemente semplice possa avere implicazioni profonde e applicazioni pratiche in diversi campi. La geometria non è solo un insieme di regole e formule, ma un modo per comprendere il mondo che ci circonda, per apprezzarne la sua armonia e per risolvere problemi in modo creativo.
Abbiamo toccato solo la superficie di questo argomento. Ci sono molte altre proprietà e teoremi relativi all'ortocentro che meritano di essere esplorati. Ad esempio, l'ortocentro è strettamente legato al circocentro e al baricentro del triangolo attraverso la retta di Eulero. Approfondire la conoscenza di queste relazioni può aprire nuove prospettive sulla geometria dei triangoli.
Ora, vi invito a riflettere: come vi può servire questa nuova conoscenza nella vostra vita, nei vostri studi o nel vostro lavoro? Quali altri concetti geometrici potrebbero aiutarvi a risolvere problemi che sembrano insolubili? Continuate ad esplorare, a sperimentare e a meravigliarvi della bellezza della matematica. Chi lo sa, magari la prossima grande scoperta geometrica la farete proprio voi!