Proiezioni Ortogonali Di Una Piramide A Base Quadrata

Ciao a tutti gli appassionati di disegno tecnico, agli studenti di architettura e ingegneria, e a chiunque sia curioso di esplorare il mondo della geometria descrittiva! Immaginate di dover comunicare la forma di un oggetto tridimensionale, come una piramide, a qualcuno che può vederlo solo su un foglio di carta. Come fare? La risposta è nelle proiezioni ortogonali, uno strumento fondamentale per rappresentare oggetti nello spazio in modo preciso e comprensibile. In questo articolo, esploreremo nel dettaglio come realizzare le proiezioni ortogonali di una piramide a base quadrata, fornendo una guida passo passo e chiarendo i concetti chiave. L'obiettivo è fornire una comprensione chiara e pratica, utile sia per chi si avvicina per la prima volta a questo argomento, sia per chi desidera consolidare le proprie conoscenze.

Cos'è la Proiezione Ortogonale?

Prima di addentrarci nella piramide, cerchiamo di capire cos'è, in termini semplici, la proiezione ortogonale. Pensatela come l'ombra di un oggetto proiettata su un piano. Immaginate una torcia che illumina un oggetto; l'ombra che si forma dietro è una proiezione dell'oggetto. Nella proiezione ortogonale, la luce della torcia è composta da raggi paralleli e perpendicolari al piano di proiezione, garantendo che le dimensioni dell'oggetto siano rappresentate in modo preciso.

La proiezione ortogonale utilizza generalmente tre piani di proiezione:

Piano Orizzontale (PO): Come suggerisce il nome, è un piano orizzontale. Immaginate il pavimento. La proiezione su questo piano è detta pianta.
Piano Verticale (PV): Un piano verticale, come un muro di fronte a voi. La proiezione su questo piano è detta prospetto o vista frontale.
Piano Laterale (PL): Un piano laterale, come un muro alla vostra destra. La proiezione su questo piano è detta vista laterale o profilo.

Questi tre piani sono tra loro perpendicolari e si intersecano formando una linea chiamata linea di terra (LT), che rappresenta l'intersezione tra il PO e il PV. La linea di terra è fondamentale per posizionare correttamente le proiezioni.

La Piramide a Base Quadrata: Le Caratteristiche

Ora, concentriamoci sulla protagonista del nostro articolo: la piramide a base quadrata. Cerchiamo di definirne le caratteristiche principali:

Base Quadrata: La base della piramide è un quadrato, con quattro lati uguali e quattro angoli retti.
Vertice (o Apice): Un punto nello spazio, non appartenente al piano della base, chiamato vertice o apice della piramide.
Facce Laterali: Quattro triangoli isosceli (o, in casi particolari, equilateri) che collegano i lati del quadrato di base al vertice.
Altezza: La distanza perpendicolare tra il vertice e il piano della base.

La posizione della piramide rispetto ai piani di proiezione influenzerà l'aspetto delle proiezioni. Ad esempio, una piramide con la base parallela al PO avrà una pianta diversa da una piramide con la base inclinata rispetto al PO.

Esecuzione delle Proiezioni Ortogonali: Passo dopo Passo

Vediamo ora come realizzare concretamente le proiezioni ortogonali di una piramide a base quadrata. Consideriamo una piramide con la base appoggiata sul PO e con un lato della base parallelo al PV. Assumiamo inoltre che l'altezza della piramide sia nota.

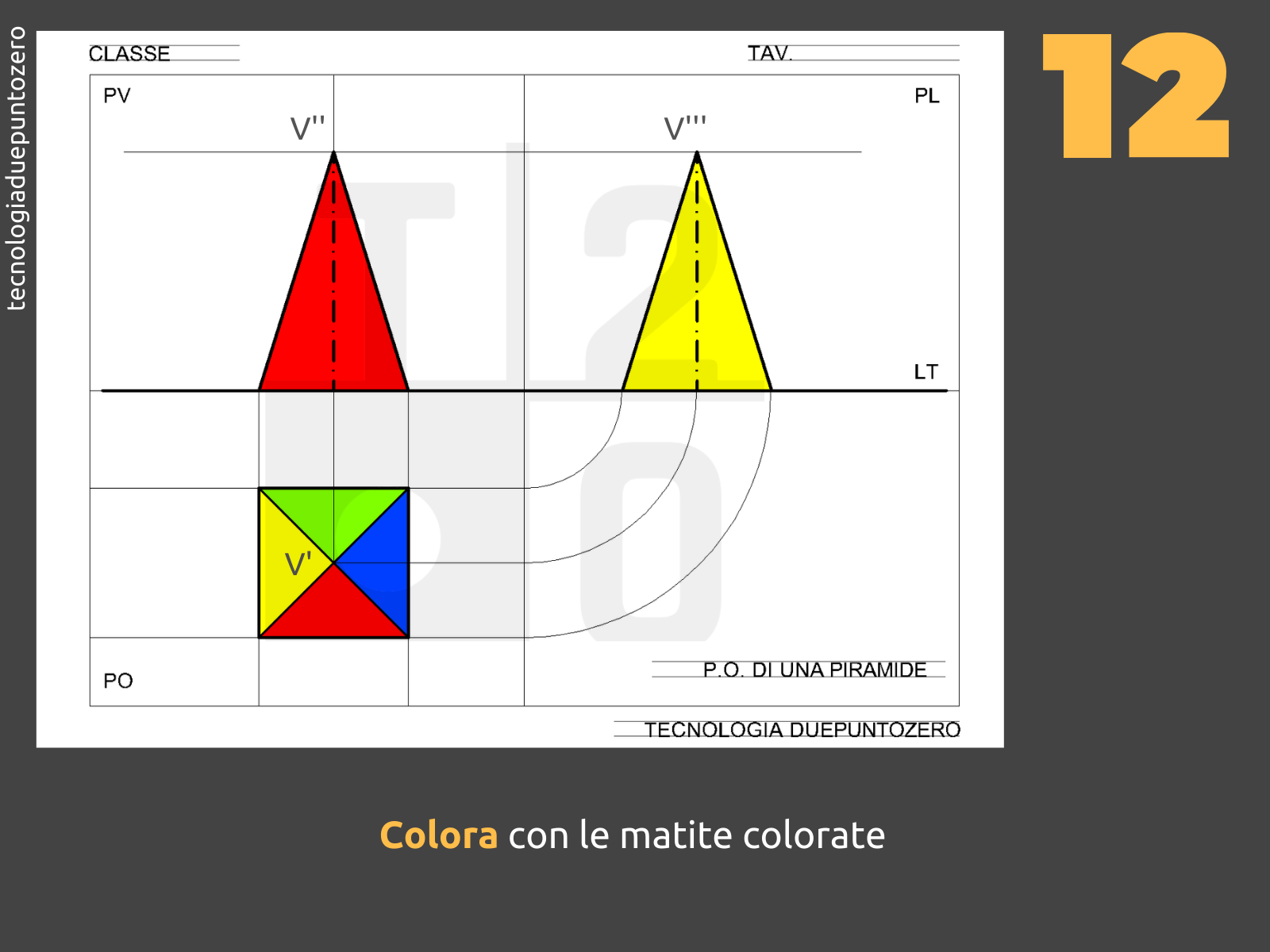
1. Rappresentazione della Base (Pianta)

Iniziamo dalla pianta, ovvero dalla proiezione sul PO. Poiché la base è appoggiata sul PO, la sua proiezione sarà il quadrato stesso. Disegniamo quindi un quadrato con le dimensioni date nel piano orizzontale. Indichiamo i vertici del quadrato con le lettere A, B, C, e D. Questi punti, essendo sul PO, coincidono con le loro proiezioni (A', B', C', D'). Indichiamo il centro del quadrato con la lettera O.

2. Rappresentazione del Vertice (in Pianta)

Il vertice della piramide (V) si proietterà sul PO nel punto O', ovvero il centro del quadrato di base. Questo perché stiamo considerando una piramide retta, cioè con il vertice perpendicolare al centro della base.

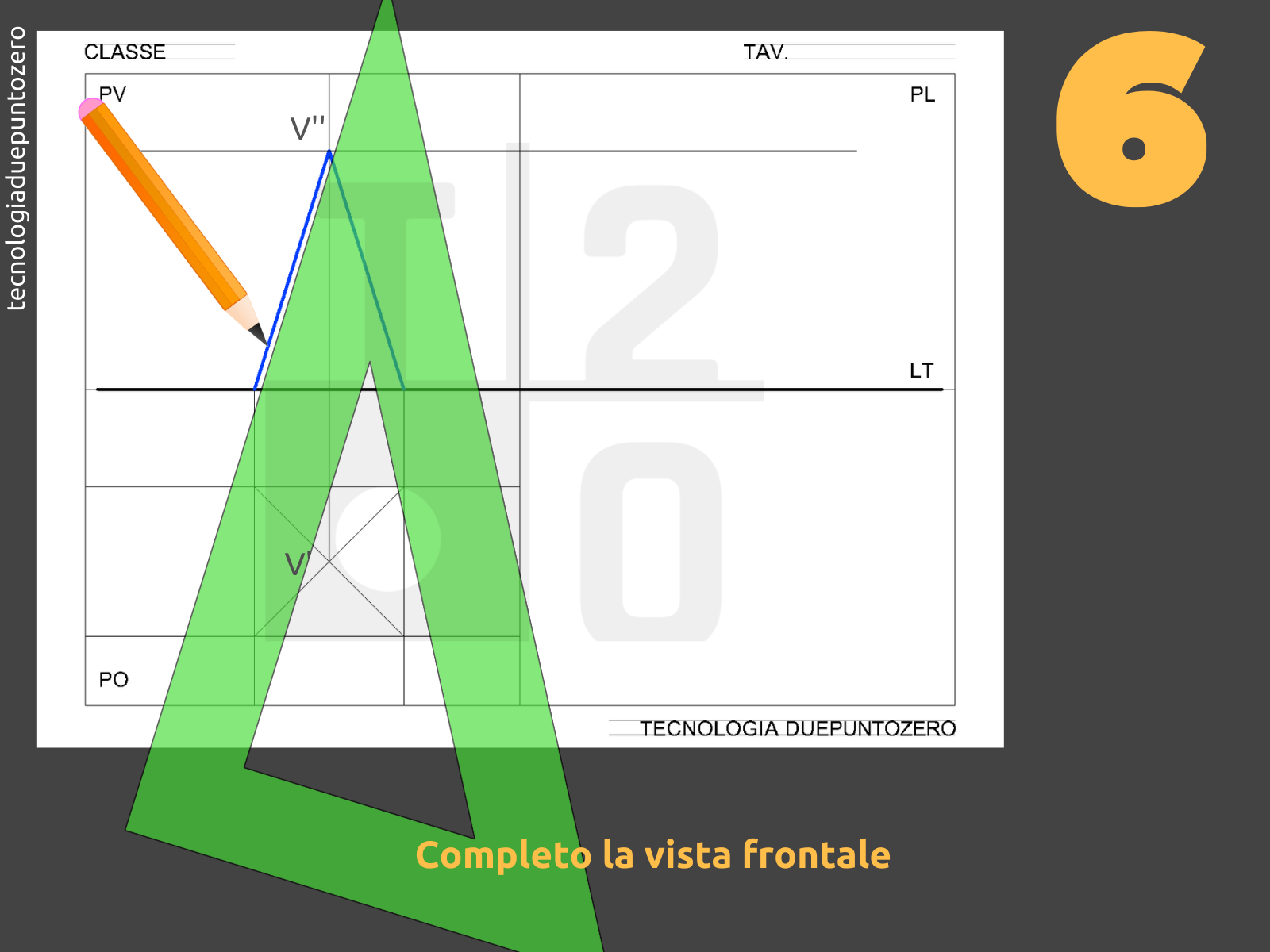
3. Rappresentazione del Prospetto (PV)

Passiamo ora al prospetto, ovvero alla proiezione sul PV. Per farlo, dobbiamo proiettare ortogonalmente i punti della base e il vertice dal PO al PV.

Tracciamo delle linee verticali (dette linee di richiamo) da A', B', C', D' e O' verso l'alto, fino ad incontrare la linea di terra (LT).
Misuriamo l'altezza della piramide.
A partire dalla LT, innalziamo una linea verticale dal punto O' (che ora chiameremo O'') sul PV, pari all'altezza della piramide. Questo punto rappresenta V'', la proiezione del vertice V sul PV.
I punti A', B', C', D' si proietteranno sulla LT e li indicheremo rispettivamente con A'', B'', C'', D''. Poiché abbiamo assunto che un lato della base sia parallelo al PV, due dei vertici (ad esempio A'' e B'') coincideranno sulla linea di terra, mentre gli altri due (C'' e D'') saranno distinti.
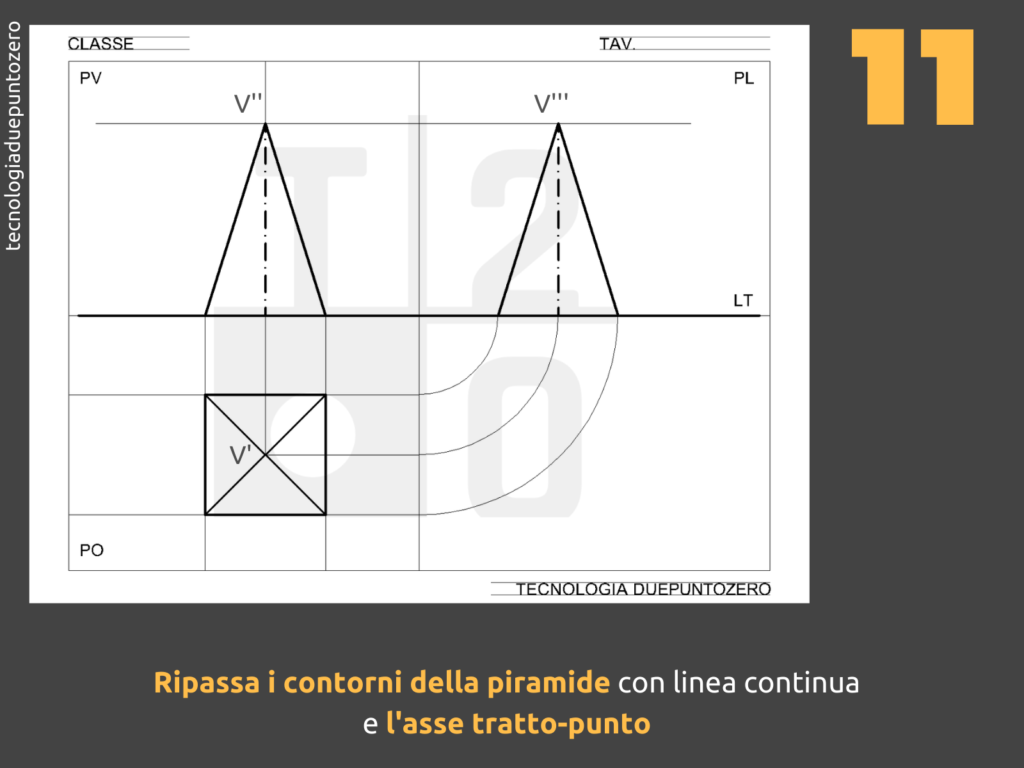
Uniamo V'' con A'', B'', C'' e D''. Questo ci darà la rappresentazione del prospetto della piramide.

Notate che alcune delle linee che rappresentano gli spigoli della piramide potrebbero essere nascoste. Convenzionalmente, le linee nascoste vengono rappresentate con una linea tratteggiata.

4. Rappresentazione del Profilo (PL)

Infine, passiamo al profilo, ovvero alla proiezione sul PL. Anche qui, utilizziamo le linee di richiamo, questa volta dal PO e dal PV al PL. Esistono diverse tecniche per "ribaltare" le misure dal PO al PL, ma una delle più comuni è l'uso del compasso.

Dal punto di intersezione tra LT e il PL, tracciamo un arco di cerchio con raggio pari alla distanza di ogni punto della base (A', B', C', D') dalla LT sul PO. Questi archi intersecheranno il PL.
Da questi punti di intersezione, innalziamo delle linee verticali sul PL.
Tracciamo linee orizzontali dai punti A'', B'', C'', D'' e V'' del prospetto verso il PL.
L'intersezione tra le linee verticali provenienti dal PO e le linee orizzontali provenienti dal PV ci daranno le proiezioni A''', B''', C''', D''' e V''' sul PL.
Uniamo V''' con A''', B''', C''' e D'''. Anche in questo caso, tenete conto delle linee nascoste.

Il profilo ci mostrerà la piramide vista di lato.

Considerazioni Importanti e Variazioni

L'esempio che abbiamo visto è il caso più semplice, con la base appoggiata sul PO e un lato parallelo al PV. Tuttavia, la piramide potrebbe essere posizionata in modi diversi, e questo influenzerebbe le proiezioni.

Piramide con Base Inclinata rispetto al PO: In questo caso, la pianta non sarà più un quadrato perfetto, ma un quadrilatero irregolare. La realizzazione del prospetto e del profilo sarà più complessa, richiedendo una maggiore attenzione alle linee di richiamo e alle misurazioni.
Piramide Ruotata rispetto al PV: Se la base della piramide è ruotata rispetto al PV, la pianta rimarrà un quadrato, ma il prospetto e il profilo saranno diversi.
Tronco di Piramide: Se la piramide viene "tagliata" da un piano parallelo alla base, otteniamo un tronco di piramide. La rappresentazione delle proiezioni di un tronco di piramide segue principi simili a quelli della piramide completa, ma richiede di considerare anche il piano di taglio.

Un altro aspetto importante è la precisione. Le proiezioni ortogonali richiedono precisione nel disegno e nelle misurazioni. L'uso di strumenti adeguati (squadre, compasso, righello) è fondamentale per ottenere un risultato accurato. Inoltre, è importante essere chiari e coerenti nella nomenclatura dei punti e delle linee.

Applicazioni Pratiche

Le proiezioni ortogonali non sono solo un esercizio teorico. Hanno numerose applicazioni pratiche in diversi campi:

Architettura: Gli architetti utilizzano le proiezioni ortogonali per rappresentare i progetti degli edifici, mostrando le piante, i prospetti e le sezioni.
Ingegneria: Gli ingegneri utilizzano le proiezioni ortogonali per rappresentare i progetti di macchinari, strutture e infrastrutture.
Design Industriale: I designer industriali utilizzano le proiezioni ortogonali per rappresentare i progetti di prodotti, mostrando le diverse viste e le dimensioni.
Grafica 3D: Anche se la grafica 3D è diventata sempre più diffusa, la comprensione delle proiezioni ortogonali è ancora utile per capire come gli oggetti tridimensionali vengono rappresentati su uno schermo bidimensionale.

Conclusione: Un Passo Verso la Comprensione dello Spazio

Speriamo che questa guida dettagliata alle proiezioni ortogonali di una piramide a base quadrata vi sia stata utile. Ricordate, la chiave per padroneggiare questo strumento è la pratica. Provate a disegnare le proiezioni ortogonali di diverse piramidi, variando la posizione e le dimensioni. Non abbiate paura di fare errori, perché è attraverso gli errori che si impara! La comprensione delle proiezioni ortogonali non solo vi aiuterà a superare gli esami, ma vi fornirà anche una solida base per comprendere e rappresentare lo spazio tridimensionale, aprendo le porte a un mondo di possibilità creative e tecniche. Buon disegno a tutti!