Proiezioni Ortogonali Di Un Prisma A Base Triangolare

Ciao! Se sei qui, probabilmente ti stai confrontando con le proiezioni ortogonali, in particolare quelle di un prisma a base triangolare. Lo so, all'inizio può sembrare un labirinto di linee e piani, ma ti assicuro che con un po' di pazienza e la giusta guida, tutto diventerà molto più chiaro. Molti studenti faticano a visualizzare queste proiezioni, a capire come un oggetto tridimensionale si traduce in una serie di disegni bidimensionali. La buona notizia è che non sei solo e che, insieme, supereremo questa sfida!

Questo articolo è pensato proprio per te. Cercherò di semplificare il concetto, usando un linguaggio accessibile e focalizzandomi sugli aspetti pratici. Non ti sommergerò di teorie astratte, ma ti fornirò gli strumenti per comprendere e realizzare le proiezioni ortogonali di un prisma a base triangolare.

Perché le Proiezioni Ortogonali Sono Importanti?

Prima di immergerci nel dettaglio, cerchiamo di capire perché le proiezioni ortogonali sono così importanti. Non sono solo un esercizio di disegno tecnico! Sono la base per la rappresentazione di oggetti tridimensionali in ambito architettonico, ingegneristico e del design. Immagina di dover costruire una casa: senza proiezioni ortogonali precise, sarebbe impossibile comunicare le dimensioni e la forma degli elementi costruttivi in modo chiaro ed efficace.

Pensa anche al design di un nuovo prodotto: le proiezioni ortogonali permettono ai designer di visualizzare il prodotto da diverse angolazioni e di comunicare le proprie idee ai produttori. In sostanza, le proiezioni ortogonali sono un linguaggio universale per la rappresentazione tecnica.

L'Impatto Reale: Dalla Teoria alla Pratica

Architettura: Progettazione di edifici, visualizzazione di spazi interni ed esterni.
Ingegneria: Realizzazione di macchinari, ponti, infrastrutture.
Design Industriale: Creazione di prodotti, prototipazione, visualizzazione 3D.
Arredamento: Progettazione di mobili, disposizione degli spazi.

Senza le proiezioni ortogonali, il mondo che ci circonda, così come lo conosciamo, sarebbe molto diverso!

Cosa Sono Esattamente le Proiezioni Ortogonali?

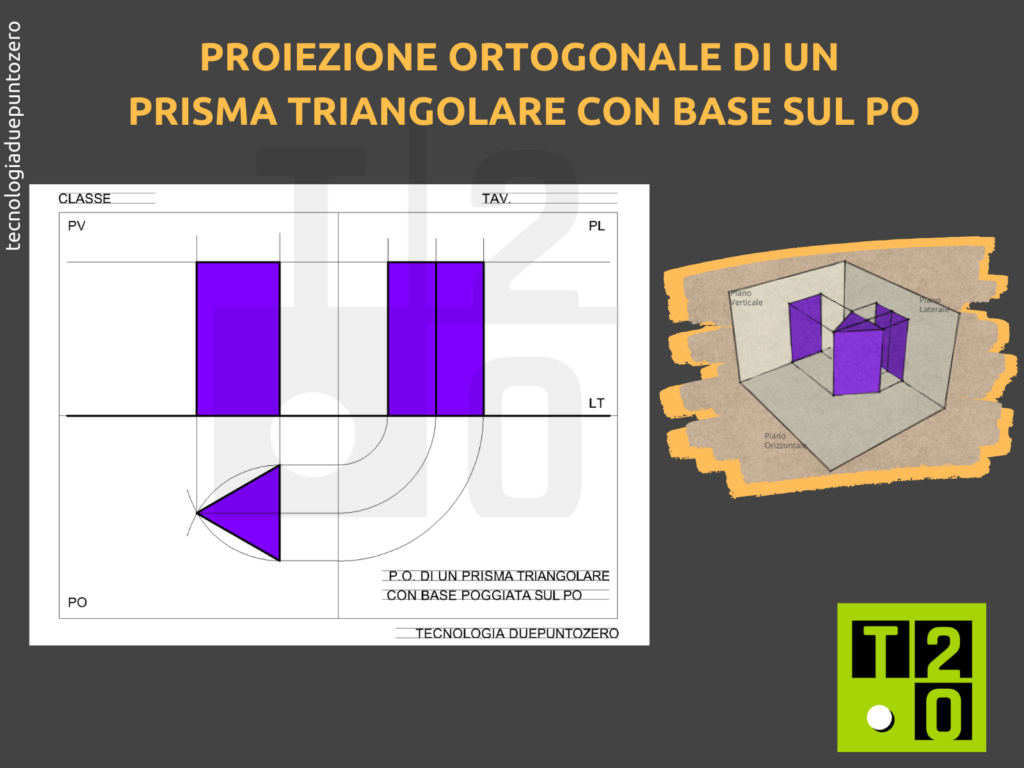
Le proiezioni ortogonali sono un metodo di rappresentazione grafica che permette di descrivere un oggetto tridimensionale su un piano bidimensionale. Si basano su tre piani di proiezione principali, ortogonali tra loro: il Piano Verticale (PV), il Piano Orizzontale (PO) e il Piano Laterale (PL).

Immagina di avere una scatola con tre pareti trasparenti, che rappresentano i piani di proiezione. L'oggetto che vuoi rappresentare è all'interno della scatola. Ora, immagina di proiettare delle linee perpendicolari (ortogonali) dall'oggetto su ciascuna delle pareti. Queste linee definiscono la forma dell'oggetto su ciascun piano.

Una volta ottenute le tre proiezioni, si "apre" la scatola, ruotando il PO verso il basso e il PL verso destra, ottenendo così una rappresentazione bidimensionale completa dell'oggetto.

I Tre Piani Fondamentali

Piano Verticale (PV): Rappresenta la vista frontale dell'oggetto.
Piano Orizzontale (PO): Rappresenta la vista dall'alto dell'oggetto.
Piano Laterale (PL): Rappresenta la vista laterale dell'oggetto.

Il Prisma a Base Triangolare: Un Esempio Pratico

Ora concentriamoci sul nostro protagonista: il prisma a base triangolare. Un prisma è un solido geometrico con due basi identiche e parallele (in questo caso, triangoli) e facce laterali rettangolari che le collegano. La chiave per proiettare correttamente un prisma è visualizzare mentalmente la sua forma e orientamento nello spazio.

Consideriamo un prisma a base triangolare con base equilatera. La sua rappresentazione in proiezioni ortogonali richiederà di disegnare le sue proiezioni sui tre piani (PV, PO e PL) tenendo conto della sua posizione nello spazio.

Passo Dopo Passo: Come Proiettare un Prisma a Base Triangolare

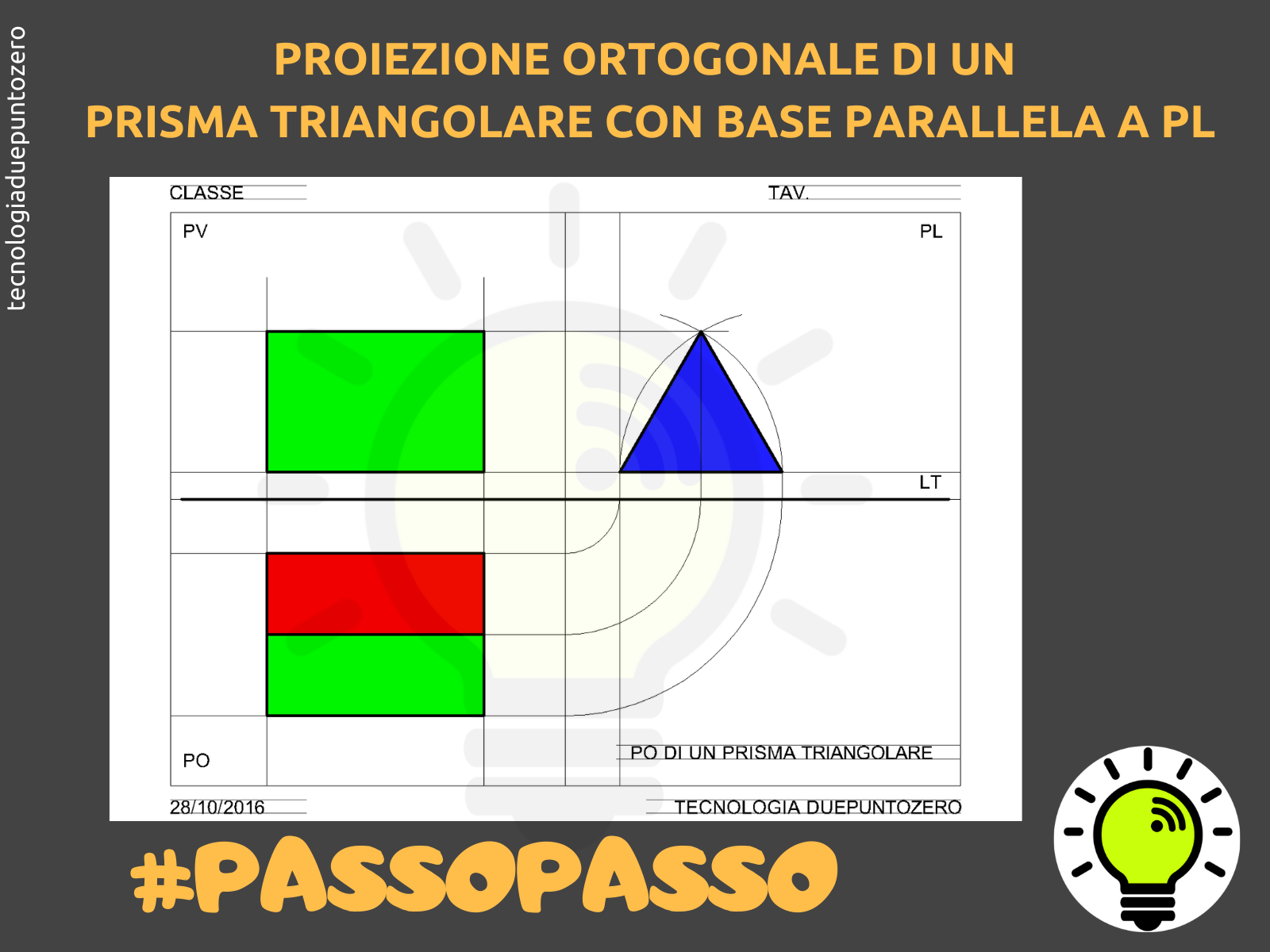
Posizionamento del Prisma: Decidi l'orientamento del prisma rispetto ai piani di proiezione. Ad esempio, puoi posizionare la base triangolare parallela al PO. Questo semplificherà la proiezione sul PO.
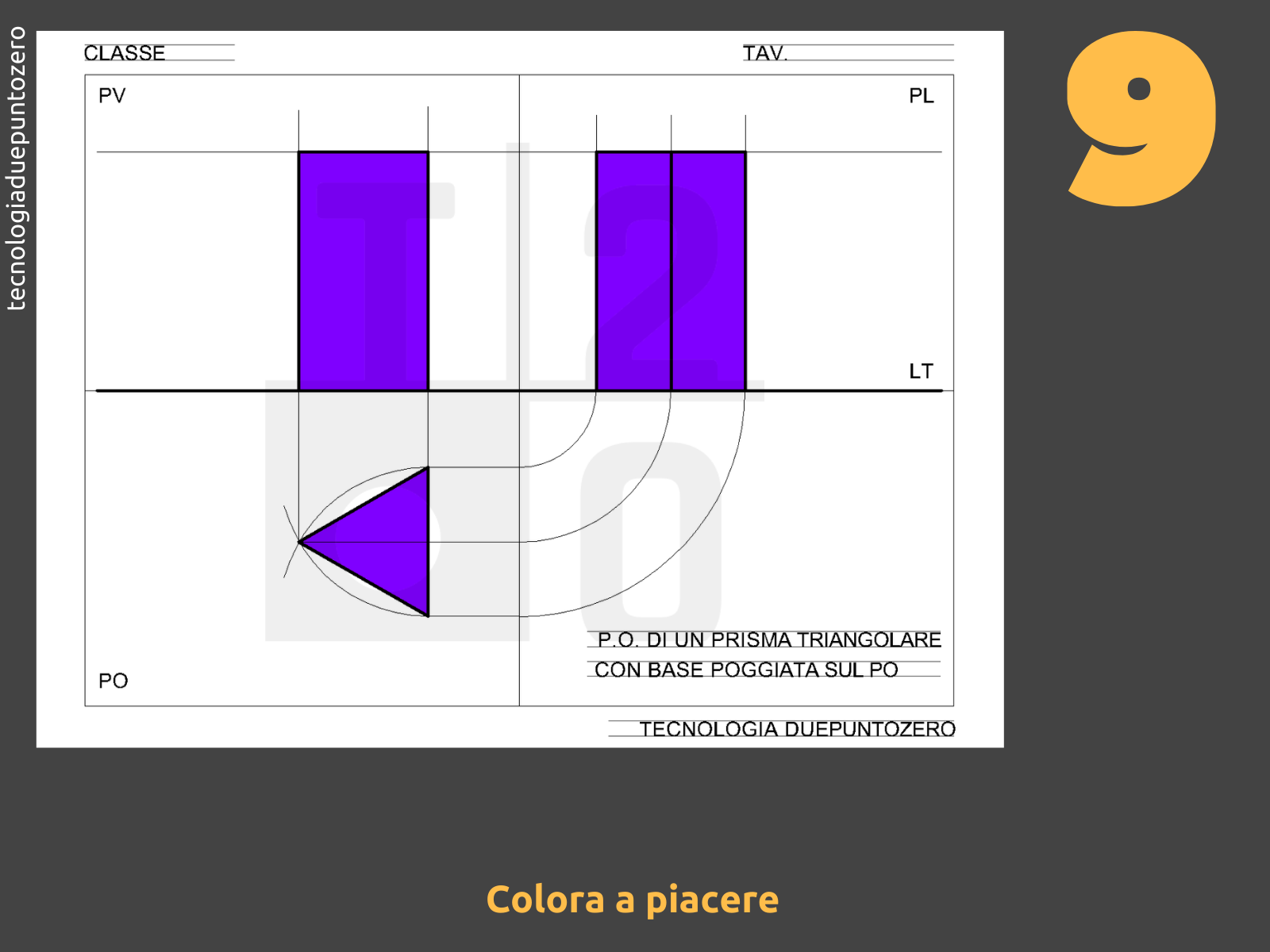
Proiezione sul Piano Orizzontale (PO): La proiezione sul PO mostrerà la vera forma della base triangolare. Disegna un triangolo equilatero (se la base è equilatera) con le dimensioni corrette. Indica i vertici con lettere (A, B, C) e i vertici corrispondenti della base superiore con lettere prime (A', B', C'). Nel PO vedrai anche l'ingombro del prisma.
Proiezione sul Piano Verticale (PV): La proiezione sul PV mostrerà un rettangolo. L'altezza del rettangolo corrisponderà all'altezza del prisma. La base del rettangolo sarà la proiezione di uno dei lati della base triangolare. Proietta i punti della base triangolare (A, B, C, A', B', C') sul PV tracciando linee verticali dal PO al PV.
Proiezione sul Piano Laterale (PL): La proiezione sul PL mostrerà un altro rettangolo, la cui altezza è uguale all'altezza del prisma. La larghezza del rettangolo dipenderà dall'orientamento del prisma. Per proiettare i punti sul PL, puoi utilizzare il metodo del ribaltamento: traccia una linea a 45 gradi dall'origine degli assi sul PO e poi proietta i punti dal PO a questa linea e poi verticalmente sul PL.

Consigli Utili

Utilizza Matite Diverse: Usa una matita più leggera per le linee di costruzione e una matita più scura per il disegno finale.
Sii Preciso: La precisione è fondamentale nelle proiezioni ortogonali. Utilizza righe, squadre e compasso per ottenere un disegno accurato.
Verifica le Proiezioni: Assicurati che le proiezioni siano coerenti tra loro. Ad esempio, l'altezza del prisma deve essere la stessa su PV e PL.
Visualizza lo Spazio: Cerca di visualizzare mentalmente il prisma nello spazio mentre lo proietti. Questo ti aiuterà a capire come le diverse viste si relazionano tra loro.

Affrontare le Difficoltà Comuni

È normale incontrare delle difficoltà quando si imparano le proiezioni ortogonali. Ecco alcuni problemi comuni e come affrontarli:

Difficoltà a Visualizzare lo Spazio: Questo è il problema più comune. Un modo per superarlo è utilizzare modelli tridimensionali, sia fisici che virtuali. Puoi anche esercitarti a disegnare oggetti semplici da diverse angolazioni.
Errori di Precisione: Gli errori di precisione possono portare a proiezioni errate. Utilizza strumenti di disegno di qualità e prenditi il tempo necessario per misurare e tracciare le linee con cura.
Confusione con le Linee di Costruzione: Può essere facile confondersi con le linee di costruzione. Utilizza matite diverse e cancella le linee non necessarie una volta completato il disegno.
Orientamento del Prisma: Scegliere l'orientamento giusto può semplificare notevolmente il processo di proiezione. Sperimenta con diverse posizioni per trovare quella più adatta.

Controventi: Un Approccio Diversificato

Alcuni potrebbero sostenere che con l'avvento del software CAD e della modellazione 3D, le proiezioni ortogonali manuali sono diventate obsolete. È vero che la tecnologia ha trasformato il modo in cui progettiamo e rappresentiamo gli oggetti, ma comprendere i principi delle proiezioni ortogonali è ancora fondamentale. La modellazione 3D si basa su questi principi. Conoscere le proiezioni ortogonali ti aiuta a capire come il software funziona, ad interpretare i risultati e a risolvere eventuali problemi. Inoltre, la capacità di disegnare proiezioni ortogonali a mano è un'abilità preziosa in situazioni in cui il software non è disponibile o quando si desidera schizzare rapidamente un'idea.

Soluzioni e Prossimi Passi

Ora hai una solida base per comprendere le proiezioni ortogonali di un prisma a base triangolare. Ricorda che la pratica è fondamentale. Non scoraggiarti se non riesci subito al primo tentativo. Continua a esercitarti e vedrai che diventerai sempre più bravo. Ecco alcuni spunti per continuare a migliorare:

Esercitati con diversi orientamenti del prisma.
Prova a proiettare prismi con basi diverse (ad esempio, un prisma a base pentagonale).
Utilizza software CAD per confrontare le tue proiezioni manuali con quelle generate dal computer.
Cerca tutorial online e video dimostrativi.
Chiedi aiuto al tuo insegnante o a un compagno di classe.

Le proiezioni ortogonali sono uno strumento potente e versatile. Padroneggiarle ti aprirà le porte a un mondo di possibilità nel campo del design, dell'ingegneria e dell'architettura. Ricorda, la chiave è la pratica e la perseveranza!

Allora, sei pronto a mettere in pratica quello che hai imparato? Quale prisma proietterai per primo?