Proiezioni Ortogonali Di Un Prisma A Base Esagonale

Le proiezioni ortogonali rappresentano uno strumento fondamentale nel disegno tecnico, nell'architettura e nell'ingegneria per la rappresentazione di oggetti tridimensionali su un piano bidimensionale. Questo metodo permette di descrivere con precisione la forma e le dimensioni di un oggetto, rendendolo facilmente comprensibile e utilizzabile per la progettazione e la costruzione. In questo articolo, esploreremo in dettaglio le proiezioni ortogonali di un prisma a base esagonale, analizzando le diverse viste e le loro caratteristiche.

Concetti Fondamentali delle Proiezioni Ortogonali

Prima di addentrarci nello specifico del prisma a base esagonale, è essenziale comprendere alcuni concetti chiave relativi alle proiezioni ortogonali. Il metodo delle proiezioni ortogonali si basa sulla proiezione di un oggetto su tre piani principali, mutuamente perpendicolari: il Piano Orizzontale (PO), il Piano Verticale (PV) e il Piano Laterale (PL). Ogni punto dell'oggetto viene proiettato ortogonalmente (cioè perpendicolarmente) su ciascuno di questi piani, creando tre viste distinte dell'oggetto.

I Piani di Proiezione

Il Piano Orizzontale (PO) rappresenta la vista dall'alto dell'oggetto, mostrando la sua pianta. Il Piano Verticale (PV) rappresenta la vista frontale, mostrando l'alzato. Il Piano Laterale (PL) rappresenta la vista laterale, offrendo una prospettiva da un lato dell'oggetto. La disposizione standard prevede che il PV sia posto di fronte all'osservatore, il PO sotto al PV (come se fosse ribaltato) e il PL a destra del PV (anch'esso ribaltato). Questo sistema di rappresentazione, noto come metodo di Monge, garantisce una visione completa e non ambigua dell'oggetto.

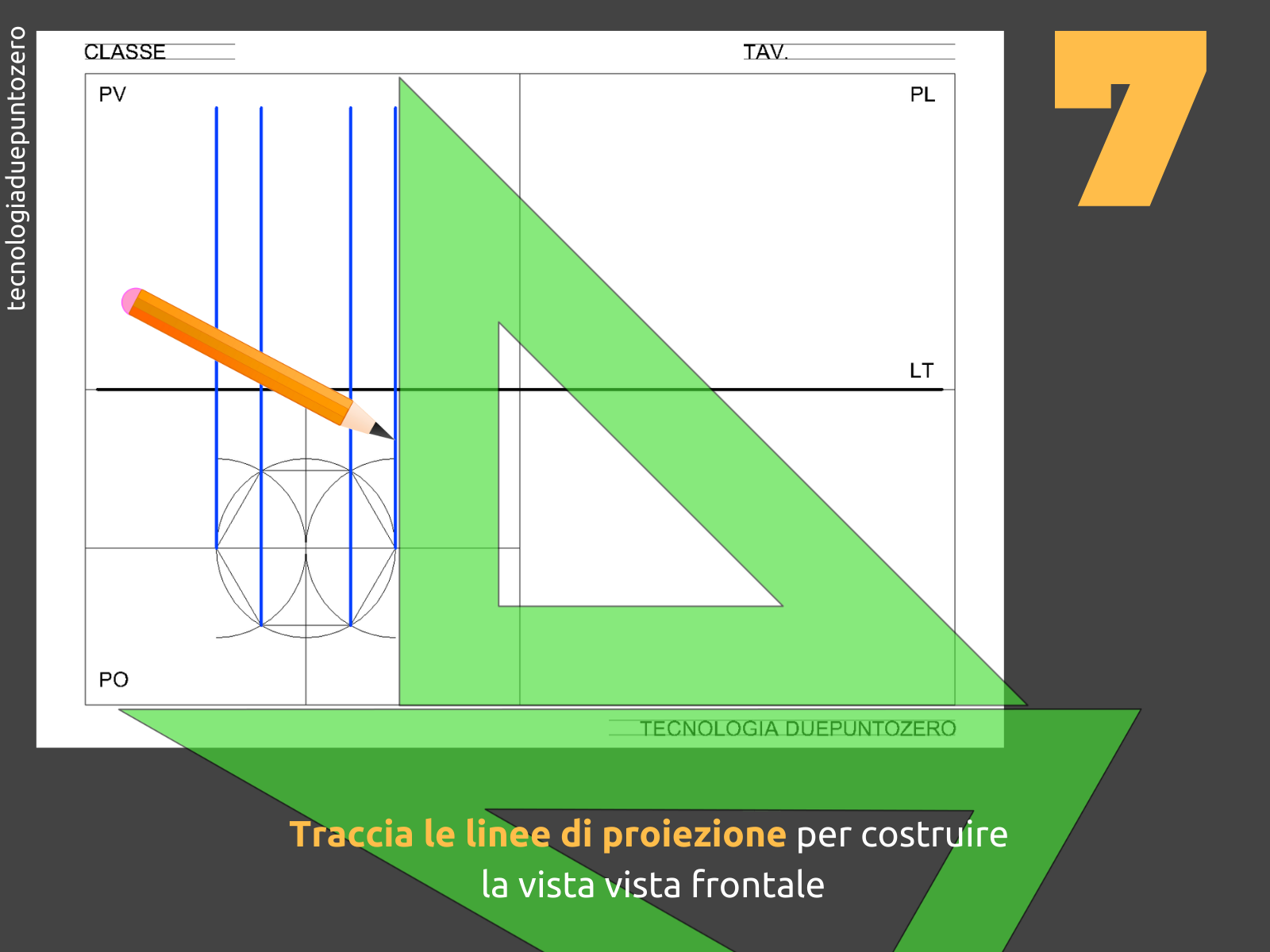
Linee di Proiezione

Le linee di proiezione sono le rette immaginarie che collegano ogni punto dell'oggetto al piano di proiezione. Queste linee sono sempre perpendicolari al piano su cui proiettano il punto. La precisione e l'accuratezza delle proiezioni ortogonali dipendono dalla corretta applicazione di queste linee. Le linee di proiezione definiscono univocamente la posizione del punto proiettato sul piano.

Ribaltamento dei Piani

Per rappresentare le tre viste (PO, PV, PL) sullo stesso foglio di disegno, i piani vengono ribaltati. Il PO viene ribaltato verso il basso, il PL viene ribaltato verso destra, mantenendo il PV come riferimento centrale. Questo processo permette di visualizzare tutte e tre le proiezioni in un'unica rappresentazione bidimensionale, semplificando la comprensione dell'oggetto tridimensionale.

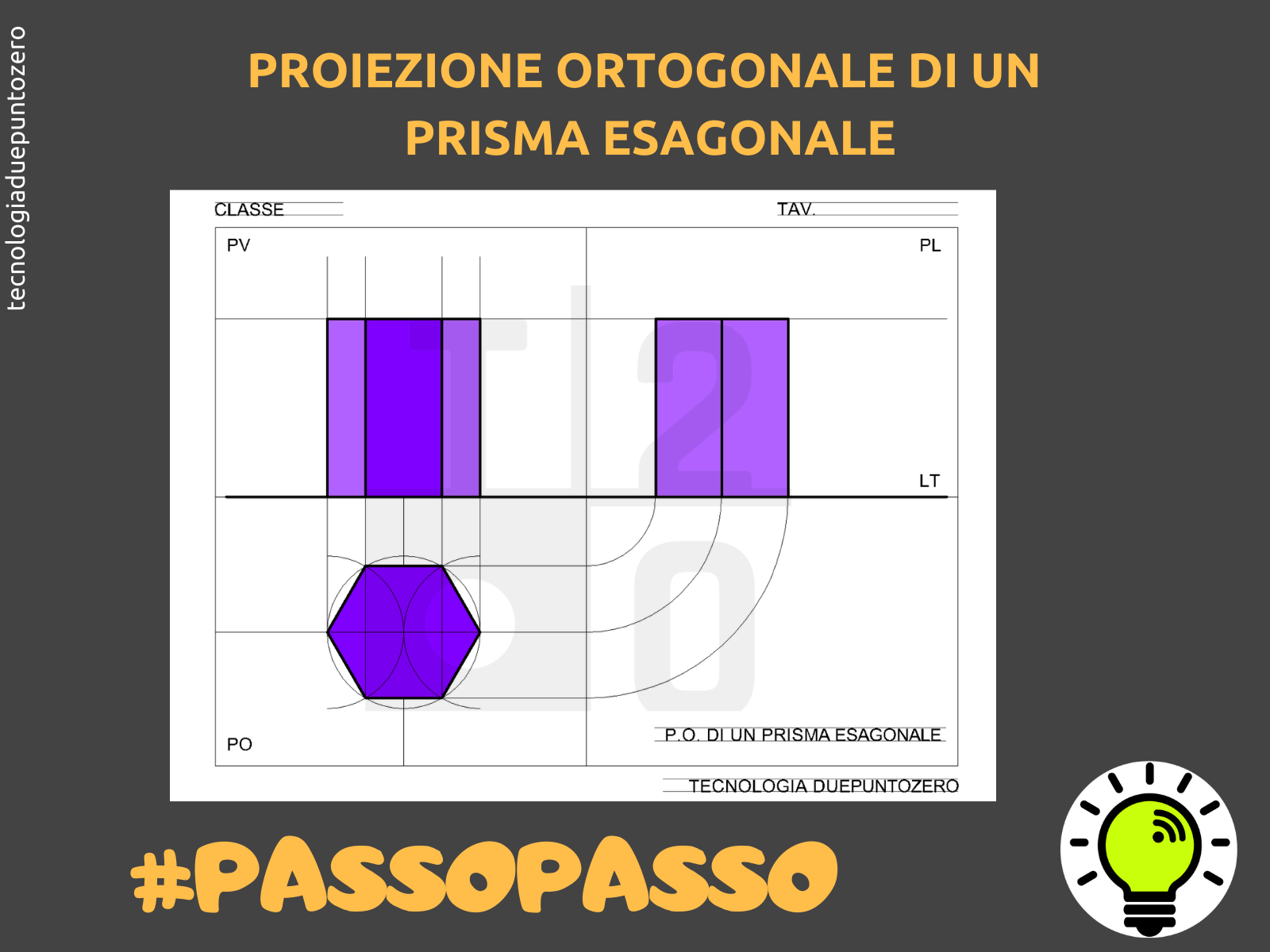
Proiezioni Ortogonali del Prisma a Base Esagonale

Un prisma a base esagonale è un solido geometrico con due basi esagonali parallele e congruenti, collegate da sei facce rettangolari. La sua rappresentazione in proiezioni ortogonali richiede una comprensione chiara della sua geometria e delle relazioni tra le sue diverse parti.

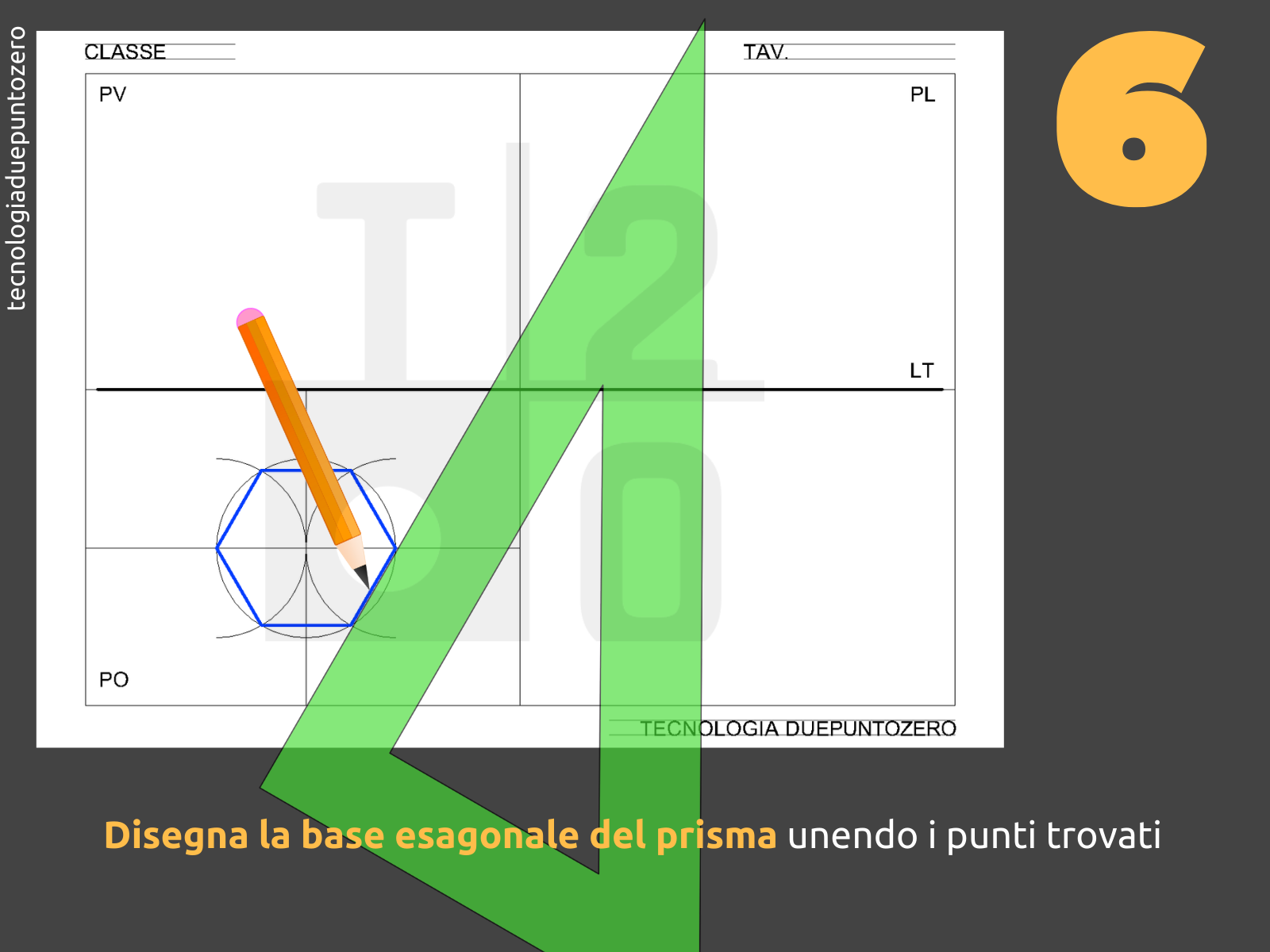
Proiezione sul Piano Orizzontale (PO)

La proiezione sul Piano Orizzontale (PO) mostra la pianta del prisma. In questo caso, si vedrà un esagono regolare. Se il prisma è posizionato con una delle sue facce esagonali parallela al PO, l'esagono sarà rappresentato nella sua vera forma e dimensione. Se, invece, il prisma è inclinato rispetto al PO, l'esagono apparirà deformato, ma le relazioni tra i suoi vertici e lati saranno comunque mantenute.

È importante disegnare l'esagono con precisione, indicando chiaramente i suoi vertici. Da ciascun vertice dell'esagono, si proietteranno delle linee verticali verso il Piano Verticale (PV), per definire la larghezza del prisma nell'alzato.

Proiezione sul Piano Verticale (PV)

La proiezione sul Piano Verticale (PV) mostra l'alzato del prisma. Se il prisma è posizionato con una delle sue facce rettangolari parallela al PV, si vedrà un rettangolo la cui base corrisponde al lato dell'esagono e l'altezza corrisponde all'altezza del prisma. Se il prisma è ruotato rispetto al PV, si vedranno due rettangoli affiancati, rappresentando due facce laterali del prisma. L'altezza del rettangolo corrisponde sempre all'altezza del prisma. Sarà necessario tracciare le linee di proiezione dai vertici dell'esagono sul PO per determinare l'esatta posizione dei vertici del rettangolo sul PV.

Nel PV, saranno visibili anche le linee di proiezione che provengono dai vertici nascosti dell'esagono, rappresentate come linee tratteggiate. Queste linee indicano le parti dell'oggetto che non sono visibili direttamente dall'osservatore.

Proiezione sul Piano Laterale (PL)

La proiezione sul Piano Laterale (PL) mostra la vista laterale del prisma. Analogamente al PV, se il prisma è posizionato con una delle sue facce rettangolari parallela al PL, si vedrà un rettangolo. Se il prisma è ruotato rispetto al PL, si vedranno due rettangoli affiancati, rappresentando due facce laterali del prisma. La larghezza di questo rettangolo (o dei due rettangoli) dipenderà dall'orientamento del prisma rispetto al PL. Anche in questo caso, l'altezza del rettangolo corrisponde all'altezza del prisma e le linee di proiezione provenienti dal PO e dal PV sono cruciali per definire correttamente la vista laterale.

Come nel PV, le linee di proiezione che provengono dai vertici nascosti dell'esagono saranno rappresentate come linee tratteggiate.

Applicazioni Pratiche e Real-World Examples

Le proiezioni ortogonali di un prisma a base esagonale trovano numerose applicazioni pratiche in diversi settori.

• Architettura: Nella progettazione di edifici, le proiezioni ortogonali vengono utilizzate per rappresentare con precisione la forma e le dimensioni di elementi architettonici come torri esagonali, lucernari a forma di prisma esagonale o dettagli decorativi.
• Ingegneria Meccanica: Nella progettazione di macchinari e componenti meccanici, i prismi a base esagonale possono essere utilizzati come elementi di collegamento, supporti o parti strutturali. Le proiezioni ortogonali sono essenziali per definire con precisione le dimensioni e le tolleranze di questi componenti. Ad esempio, i bulloni e le viti con testa esagonale sono comunemente rappresentati utilizzando proiezioni ortogonali per specificare le loro dimensioni esatte.
• Design Industriale: Nel design di prodotti, i prismi a base esagonale possono essere utilizzati per creare oggetti con forme uniche e accattivanti. Le proiezioni ortogonali sono utilizzate per visualizzare e comunicare il design del prodotto a produttori e clienti. Pensiamo a un packaging di profumo a forma di prisma esagonale: la sua rappresentazione tecnica necessiterebbe di proiezioni ortogonali per la sua corretta produzione.
• Geometria Descrittiva: L'apprendimento delle proiezioni ortogonali è fondamentale nello studio della geometria descrittiva, una disciplina che si occupa della rappresentazione di oggetti tridimensionali su un piano bidimensionale. La comprensione delle proiezioni ortogonali è essenziale per la risoluzione di problemi geometrici e la visualizzazione di oggetti complessi.

Considerazioni Aggiuntive

È importante ricordare che la precisione e l'accuratezza sono fondamentali nella realizzazione delle proiezioni ortogonali. L'utilizzo di strumenti di disegno adeguati, come squadrette, compassi e righe, è essenziale per garantire la correttezza delle proiezioni. Inoltre, è importante prestare attenzione alla disposizione dei piani di proiezione e alla corretta applicazione delle linee di proiezione. La chiarezza nella rappresentazione è un altro aspetto cruciale. Le linee devono essere nitide e distinte, e le parti nascoste devono essere chiaramente indicate con linee tratteggiate. L'utilizzo di convenzioni grafiche standardizzate facilita la comprensione delle proiezioni da parte di altri disegnatori e progettisti.

Un ulteriore aspetto da considerare è la scelta dell'orientamento del prisma rispetto ai piani di proiezione. La scelta dell'orientamento può influenzare la complessità delle proiezioni e la facilità di comprensione della forma dell'oggetto. In generale, è consigliabile scegliere un orientamento che permetta di visualizzare il maggior numero possibile di dettagli e di ridurre il numero di linee tratteggiate.

Conclusione

Le proiezioni ortogonali di un prisma a base esagonale rappresentano un esempio concreto dell'applicazione di questo fondamentale strumento di rappresentazione grafica. Attraverso la comprensione dei concetti fondamentali e la pratica nella realizzazione delle proiezioni, è possibile acquisire le competenze necessarie per rappresentare con precisione e chiarezza oggetti tridimensionali su un piano bidimensionale. Questo skill è essenziale per chiunque lavori nel campo del disegno tecnico, dell'architettura, dell'ingegneria e del design. Continua ad esercitarti con diverse forme e orientamenti per perfezionare la tua tecnica e ampliare la tua capacità di visualizzazione spaziale! Considera di approfondire lo studio della geometria descrittiva per una comprensione ancora più completa delle proiezioni ortogonali e delle loro applicazioni.