Proiezione Ortogonale Di Un Prisma A Base Triangolare

La proiezione ortogonale è un metodo fondamentale nel disegno tecnico e nella geometria descrittiva. Permette di rappresentare oggetti tridimensionali su un piano bidimensionale, fornendo informazioni precise sulle loro dimensioni e forma. In questo articolo, esploreremo in dettaglio la proiezione ortogonale di un prisma a base triangolare, illustrandone i principi fondamentali e le applicazioni pratiche.
Fondamenti della Proiezione Ortogonale
La proiezione ortogonale si basa sull'idea di proiettare un oggetto da un punto di vista infinitamente distante su un piano di proiezione. Le linee di proiezione, o raggi proiettanti, sono perpendicolari al piano di proiezione. Questo garantisce che le dimensioni e le forme dell'oggetto siano rappresentate in modo fedele, senza distorsioni prospettiche.
I Piani di Proiezione
Nel sistema di proiezione ortogonale, si utilizzano tipicamente tre piani di proiezione principali:
- Piano Orizzontale (PO): Rappresenta la vista dall'alto dell'oggetto.
- Piano Verticale (PV): Rappresenta la vista frontale dell'oggetto.
- Piano Laterale (PL): Rappresenta la vista laterale dell'oggetto.
Questi piani sono mutuamente perpendicolari e si intersecano lungo le linee di terra. La linea di terra è l'intersezione tra il PO e il PV, e svolge un ruolo cruciale nell'allineamento delle proiezioni.
La Rappresentazione di un Punto
La proiezione di un punto nello spazio su ciascun piano di proiezione determina le sue coordinate. Queste coordinate sono solitamente denominate quota (distanza dal PO), aggetto (distanza dal PV) e lontananza (distanza dal PL). La combinazione di queste coordinate permette di ricostruire la posizione del punto nello spazio tridimensionale.
Proiezione Ortogonale di un Prisma a Base Triangolare
Un prisma a base triangolare è un solido geometrico composto da due triangoli congruenti e paralleli (le basi) e tre facce rettangolari che collegano i lati corrispondenti dei triangoli. La sua proiezione ortogonale richiede la rappresentazione delle sue basi triangolari e delle sue facce laterali sui tre piani di proiezione.
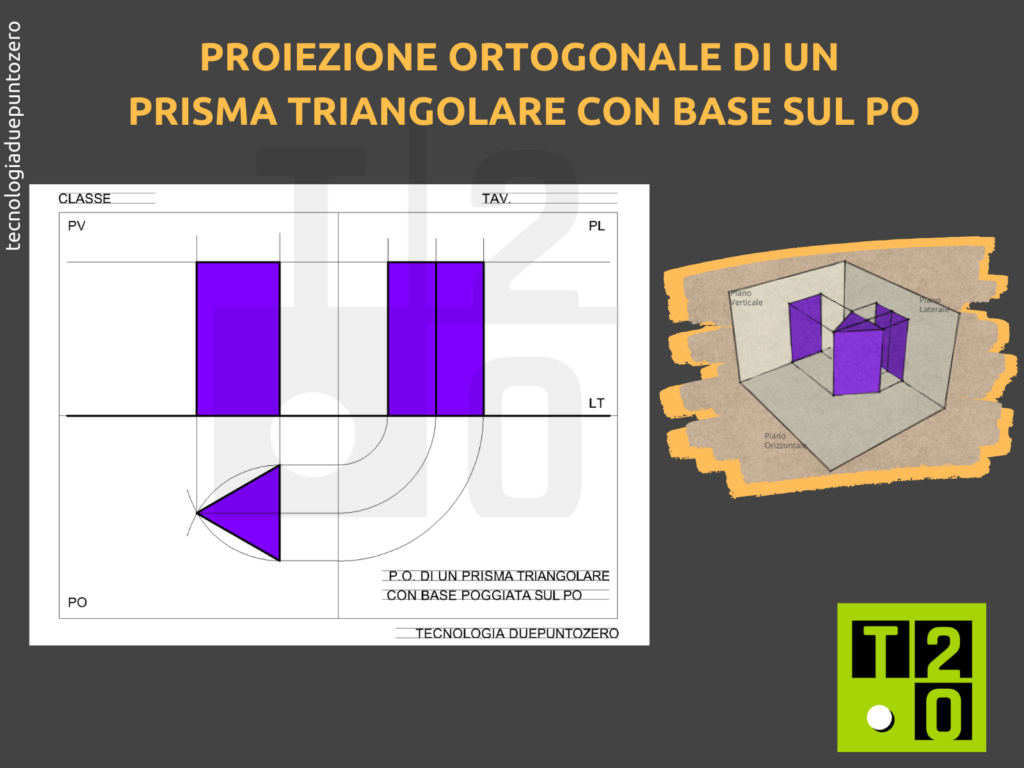
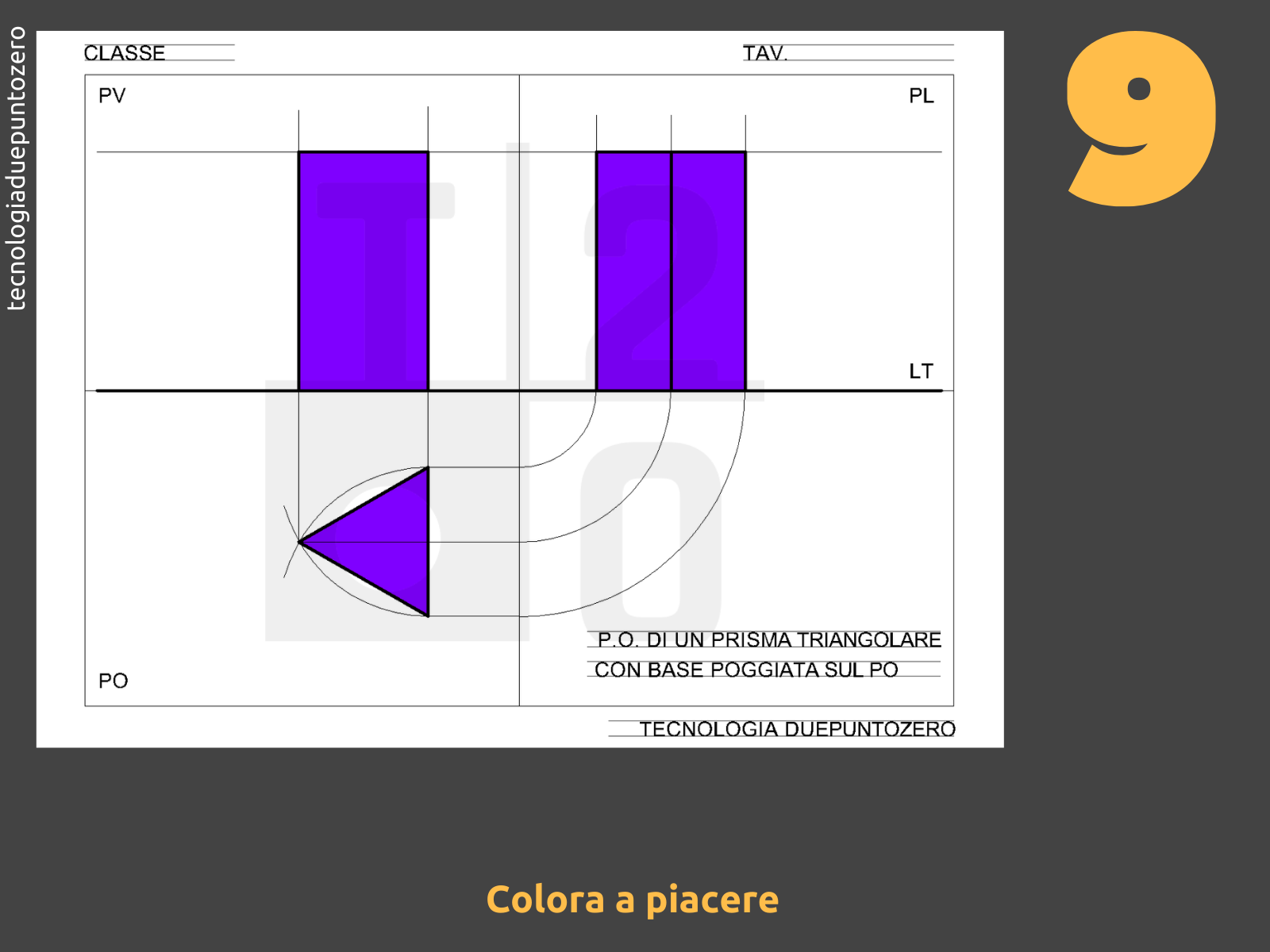
Proiezione sul Piano Orizzontale (PO)
La proiezione sul PO mostra la vista dall'alto del prisma. La base triangolare apparirà come un triangolo, a meno che una delle sue facce non sia parallela al PO. In quel caso, la proiezione potrebbe degenerare in una linea. Se il prisma è posizionato con la sua base parallela al PO, il triangolo proiettato manterrà le sue vere dimensioni e forma. Le facce laterali appariranno come rettangoli, la cui larghezza corrisponderà alla lunghezza dei lati del triangolo di base e la cui lunghezza sarà pari all'altezza del prisma.
Importante: Nel PO, si rappresentano anche le altezze relative dei vertici del prisma, utilizzando linee di richiamo che collegano la proiezione sul PO con le proiezioni sugli altri piani.
Proiezione sul Piano Verticale (PV)
La proiezione sul PV mostra la vista frontale del prisma. Se il prisma è posizionato con una delle sue facce rettangolari parallela al PV, questa faccia apparirà come un rettangolo in vera forma e dimensione. Le basi triangolari, a meno che non siano perpendicolari al PV, appariranno come linee. Se una delle basi è perpendicolare al PV, si proietterà come un segmento di retta.
La proiezione sul PV è fondamentale per determinare l'altezza del prisma. L'altezza sarà la dimensione verticale del rettangolo che rappresenta una delle facce laterali, se questa è parallela al PV.
Proiezione sul Piano Laterale (PL)
La proiezione sul PL mostra la vista laterale del prisma. La rappresentazione sul PL è simile a quella sul PV, ma offre una prospettiva diversa. Se una delle facce laterali è parallela al PL, essa apparirà come un rettangolo in vera forma e dimensione. Come per il PV, le basi triangolari appariranno come linee, a meno che non siano perpendicolari al PL.
La proiezione sul PL fornisce informazioni aggiuntive sulla profondità del prisma e sulle relazioni tra le sue diverse facce.
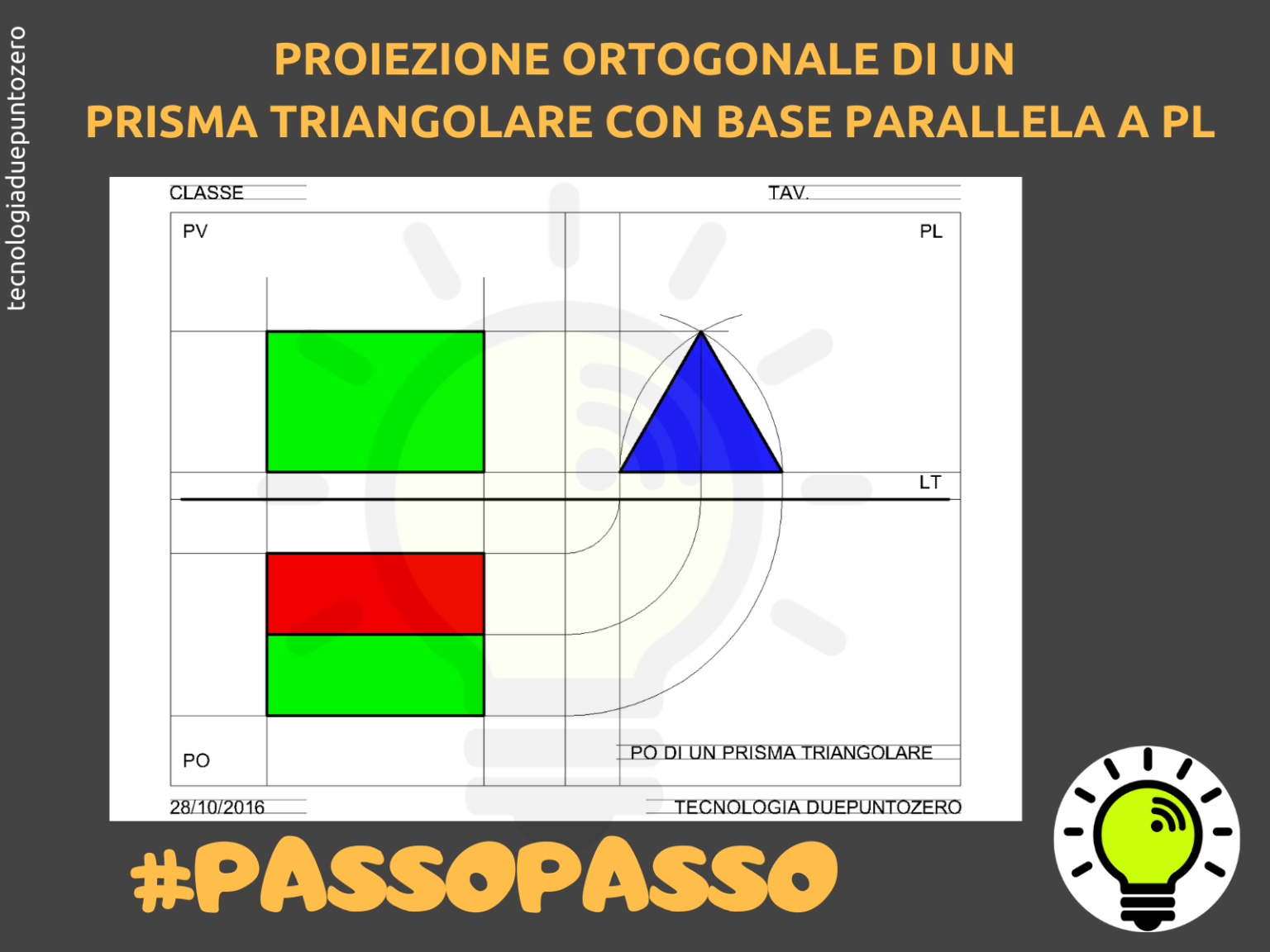
Esempio Pratico: Un Prisma con Base Triangolare Equilatera
Consideriamo un prisma a base triangolare equilatera, con lato di base di 5 cm e altezza di 10 cm. Supponiamo che il prisma sia posizionato con una delle sue facce laterali parallela al PV e con la sua base parallela al PO.
- PO: La proiezione sarà un triangolo equilatero di 5 cm di lato.
- PV: La proiezione sarà un rettangolo di 5 cm di larghezza e 10 cm di altezza.
- PL: La proiezione sarà un rettangolo di altezza 10 cm e larghezza pari all'altezza del triangolo equilatero (circa 4.33 cm).
Attraverso le linee di richiamo, possiamo collegare le proiezioni sui diversi piani, assicurando che le informazioni siano coerenti e accurate.
Applicazioni Pratiche
La proiezione ortogonale di un prisma a base triangolare, e in generale la proiezione ortogonale di solidi geometrici, trova numerose applicazioni in diversi campi:
- Architettura: Nella progettazione di edifici, la proiezione ortogonale è utilizzata per creare piante, prospetti e sezioni che rappresentano le dimensioni e le forme degli elementi architettonici.
- Ingegneria Meccanica: Nella progettazione di macchinari e componenti meccanici, la proiezione ortogonale è utilizzata per creare disegni tecnici che specificano le dimensioni, le tolleranze e le caratteristiche dei pezzi.
- Design Industriale: Nella progettazione di prodotti, la proiezione ortogonale è utilizzata per creare modelli tridimensionali che possono essere visualizzati e valutati da diversi punti di vista.
- Grafica Computerizzata: Sebbene i moderni software utilizzino rendering 3D, la comprensione dei principi di proiezione ortogonale è fondamentale per controllare le viste e generare disegni tecnici.
Ad esempio, la progettazione di un elemento strutturale come una trave a forma di prisma triangolare per un ponte richiede l'uso di proiezioni ortogonali per definire le sue dimensioni e angolazioni, garantendo la sua stabilità e resistenza.
Oltre la Teoria: Consigli Pratici
Ecco alcuni consigli pratici per realizzare proiezioni ortogonali accurate:
- Utilizzare strumenti di disegno di precisione: Squadre, compassi e righelli graduati sono essenziali per garantire l'accuratezza delle proiezioni.
- Comprendere le convenzioni di disegno tecnico: Familiarizzarsi con le norme e le convenzioni relative alla rappresentazione di linee, quote e simboli.
- Praticare regolarmente: La pratica è fondamentale per sviluppare la capacità di visualizzare oggetti tridimensionali e rappresentarli accuratamente su un piano bidimensionale.
- Utilizzare software CAD: I software di Computer-Aided Design (CAD) semplificano il processo di creazione di proiezioni ortogonali, automatizzando molti passaggi e riducendo il rischio di errori. Anche se si usa CAD, la comprensione dei principi alla base è *cruciale*.
- Controllare le proiezioni: Verificare sempre la coerenza tra le proiezioni sui diversi piani. Errori in una proiezione si rifletteranno anche nelle altre.
La chiave per una proiezione ortogonale efficace è la comprensione profonda dei concetti geometrici e l'applicazione rigorosa delle tecniche di disegno.
Conclusione
La proiezione ortogonale di un prisma a base triangolare è un esercizio fondamentale nel disegno tecnico e nella geometria descrittiva. Comprendendo i principi fondamentali della proiezione ortogonale e applicando le tecniche corrette, è possibile rappresentare accuratamente oggetti tridimensionali su un piano bidimensionale, fornendo informazioni precise sulle loro dimensioni, forma e posizione. Questa capacità è essenziale per professionisti in diversi campi, tra cui architettura, ingegneria meccanica, design industriale e grafica computerizzata.
Invitiamo i lettori a esercitarsi nella realizzazione di proiezioni ortogonali di diversi solidi geometrici, sperimentando con diverse posizioni e orientamenti. La pratica costante è la chiave per padroneggiare questa tecnica e sfruttare appieno il suo potenziale.