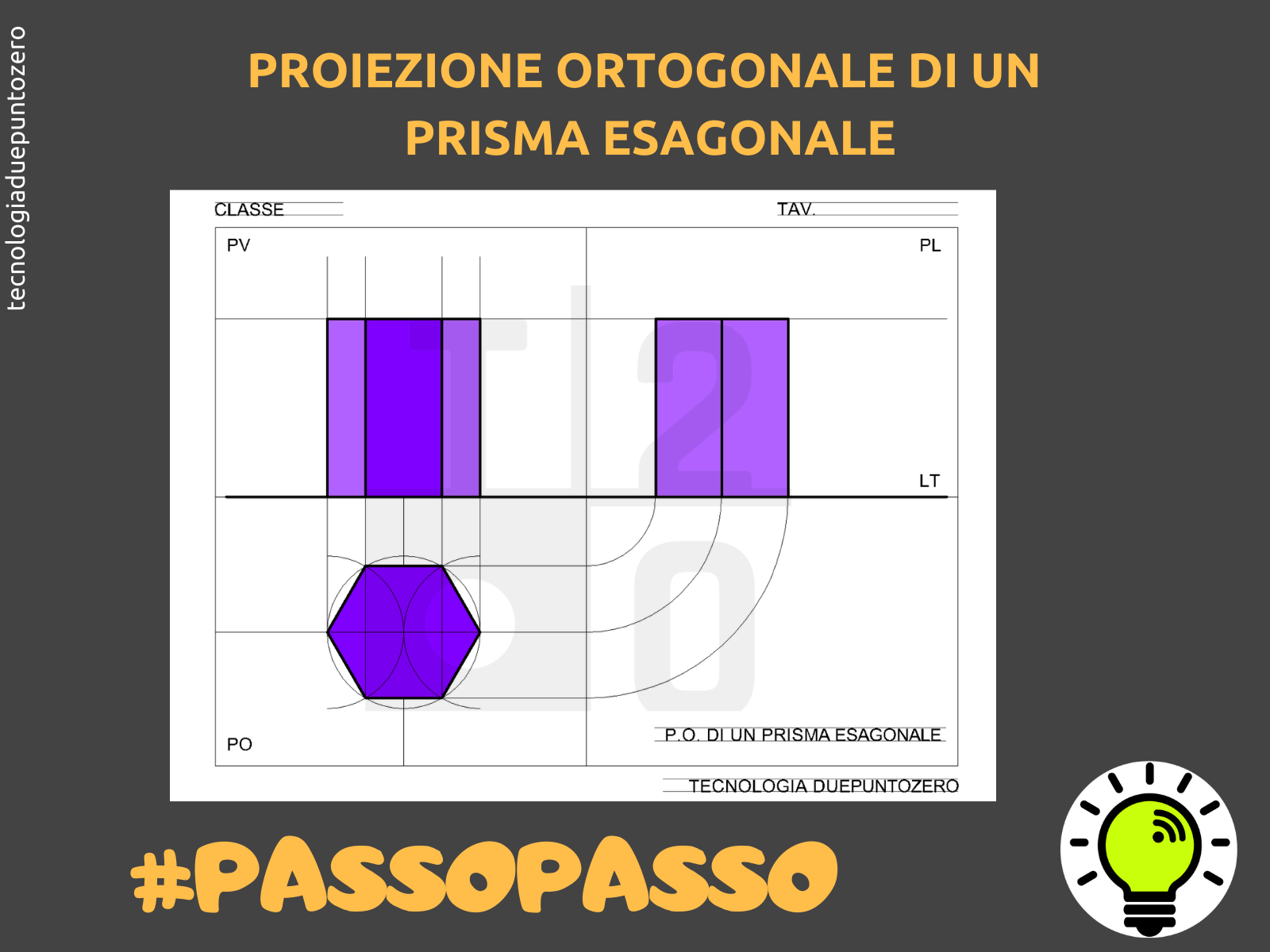
Proiezione Ortogonale Di Un Prisma A Base Quadrata

Immagina di voler costruire un modellino di un edificio, un cubo di Rubik, o anche semplicemente di dover descrivere un oggetto tridimensionale a qualcuno che lo deve ricostruire a partire da un disegno. Come faresti a rappresentare con precisione le sue forme e dimensioni su un foglio di carta, che è bidimensionale? Ecco dove entra in gioco la proiezione ortogonale, un potente strumento della geometria descrittiva.

Questo articolo è pensato per studenti di scuole medie superiori, appassionati di disegno tecnico e chiunque voglia comprendere come rappresentare oggetti tridimensionali in modo preciso e univoco. Cercheremo di rendere il concetto della proiezione ortogonale di un prisma a base quadrata il più chiaro e comprensibile possibile, utilizzando esempi pratici e un linguaggio accessibile.

Cos'è la Proiezione Ortogonale?

La proiezione ortogonale è un metodo di rappresentazione grafica che permette di descrivere un oggetto tridimensionale su un piano bidimensionale attraverso proiezioni perpendicolari. In altre parole, immaginiamo di illuminare l'oggetto con raggi di luce paralleli tra loro e perpendicolari al piano di proiezione. L'ombra che l'oggetto proietta sul piano è la sua proiezione ortogonale.

Il termine "ortogonale" deriva dal greco "orthos" (retto) e "gonia" (angolo), sottolineando che i raggi proiettanti formano un angolo retto con il piano di proiezione. Questo garantisce che la proiezione mantenga le proporzioni dell'oggetto nella direzione parallela al piano.

I Piani di Proiezione

Per rappresentare completamente un oggetto tridimensionale, si utilizzano generalmente tre piani di proiezione, disposti ortogonalmente tra loro:

• Piano Orizzontale (PO): Rappresenta la vista dall'alto (pianta) dell'oggetto.
• Piano Verticale (PV): Rappresenta la vista frontale (prospetto) dell'oggetto.
• Piano Laterale (PL): Rappresenta la vista laterale (fianco) dell'oggetto.

Questi tre piani, una volta "aperti" e disposti su un unico foglio, ci permettono di avere una rappresentazione completa dell'oggetto, mostrando le sue dimensioni in tutte e tre le direzioni spaziali.

Il Prisma a Base Quadrata: Un Esempio Pratico

Concentriamoci ora sul prisma a base quadrata. Un prisma è un solido geometrico delimitato da due basi poligonali congruenti e parallele, e da facce laterali che sono parallelogrammi. Nel nostro caso, le basi sono due quadrati e le facce laterali sono rettangoli. Questo solido è perfetto per illustrare il concetto di proiezione ortogonale per la sua semplicità geometrica e la chiarezza con cui si possono visualizzare le sue proiezioni.

Proiezione Ortogonale del Prisma

Vediamo ora come proiettare ortogonalmente il nostro prisma sui tre piani di proiezione:

1. Proiezione sul Piano Orizzontale (PO):

Immagina di guardare il prisma dall'alto. Cosa vedresti? Vedresti il quadrato che forma la base superiore del prisma. Questo quadrato sarà la proiezione del prisma sul Piano Orizzontale. La posizione del quadrato sul PO dipenderà da come il prisma è orientato nello spazio rispetto ai piani di proiezione. Se una delle facce laterali del prisma è parallela al PV, allora il quadrato sul PO avrà i lati paralleli e perpendicolari alla linea di terra (la linea di intersezione tra PO e PV).

Ricorda: la proiezione sul PO ci fornisce informazioni sulla forma della base e sulla posizione del prisma rispetto al piano orizzontale.

2. Proiezione sul Piano Verticale (PV):

Ora immagina di guardare il prisma frontalmente. Vedresti un rettangolo. L'altezza di questo rettangolo corrisponde all'altezza del prisma, mentre la base del rettangolo corrisponde alla lunghezza del lato del quadrato di base. La posizione del rettangolo sul PV dipenderà, come detto prima, dall'orientamento del prisma. Se una faccia laterale è parallela al PV, allora il rettangolo avrà la base parallela alla linea di terra.

La proiezione sul PV ci fornisce informazioni sull'altezza del prisma e sulla sua posizione rispetto al piano verticale.

3. Proiezione sul Piano Laterale (PL):

Infine, immagina di guardare il prisma di lato. Anche in questo caso, vedresti un rettangolo. Le dimensioni di questo rettangolo saranno identiche a quelle del rettangolo proiettato sul PV. Questo perché il prisma a base quadrata ha le facce laterali uguali.

La proiezione sul PL ci fornisce una vista laterale del prisma e conferma le informazioni sull'altezza e sulla forma della base.

Disegno delle Proiezioni

Dopo aver immaginato le proiezioni, è necessario disegnarle. Ecco alcuni consigli per un disegno corretto:

• Linea di Terra (LT): Disegna una linea orizzontale, che rappresenta l'intersezione tra PO e PV. Questa linea è fondamentale per allineare le proiezioni.
• Allineamento: Le proiezioni sui tre piani devono essere allineate tra loro. Ad esempio, i punti che rappresentano i vertici del prisma devono essere proiettati verticalmente dal PO al PV e orizzontalmente dal PV al PL.
• Convenzioni: Utilizza linee continue per i contorni visibili e linee tratteggiate per i contorni nascosti. Questo aiuta a distinguere le parti dell'oggetto che sono visibili da quelle che non lo sono in ciascuna proiezione.
• Quote: Aggiungi le quote (indicazioni delle misure) per specificare le dimensioni del prisma. Questo è fondamentale per una rappresentazione completa e precisa.

Esempio Pratico Passo-Passo

Consideriamo un prisma a base quadrata con lato di base di 3 cm e altezza di 5 cm. Supponiamo che il prisma sia posizionato con una faccia laterale parallela al PV e con la base appoggiata sul PO.

1. PO (Pianta): Disegna un quadrato di 3 cm di lato. I lati del quadrato saranno paralleli e perpendicolari alla LT.
2. PV (Prospetto): Traccia una linea verticale dalla LT fino a 5 cm di altezza. Disegna un rettangolo con base di 3 cm (uguale al lato del quadrato) e altezza di 5 cm. La base del rettangolo coinciderà con la LT.
3. PL (Fianco): Trasporta l'altezza del rettangolo dal PV al PL. Disegna un altro rettangolo con la stessa base e altezza del rettangolo sul PV.
4. Allineamento: Assicurati che i vertici corrispondenti sui tre piani siano allineati verticalmente e orizzontalmente.
5. Quote: Aggiungi le quote per indicare il lato del quadrato (3 cm) e l'altezza del prisma (5 cm).

Perché la Proiezione Ortogonale è Importante?

La proiezione ortogonale è uno strumento fondamentale in diversi campi, tra cui:

• Disegno Tecnico: Utilizzata per la rappresentazione di progetti architettonici, meccanici ed elettronici.
• Architettura: Essenziale per la progettazione e la visualizzazione di edifici.
• Ingegneria: Utilizzata per la progettazione di macchinari, infrastrutture e componenti elettronici.
• Design: Utilizzata per la progettazione di prodotti industriali e di interni.
• Grafica 3D: I principi della proiezione ortogonale sono alla base della creazione di modelli 3D e della visualizzazione di oggetti virtuali.

Comprendere la proiezione ortogonale ti permette di interpretare correttamente disegni tecnici, comunicare efficacemente le tue idee progettuali e sviluppare una solida base per lo studio di discipline tecniche e artistiche.

Consigli Aggiuntivi

• Pratica: Il miglior modo per padroneggiare la proiezione ortogonale è la pratica. Prova a proiettare diversi oggetti, variando la loro posizione e orientamento rispetto ai piani di proiezione.
• Software CAD: Esplora l'uso di software CAD (Computer-Aided Design) per creare e visualizzare proiezioni ortogonali in modo più efficiente.
• Risorse Online: Approfitta delle numerose risorse online disponibili, come tutorial, video e esercizi interattivi.
• Libri di Testo: Consulta libri di testo di disegno tecnico e geometria descrittiva per approfondire la teoria e la pratica della proiezione ortogonale.

Conclusione

La proiezione ortogonale del prisma a base quadrata è un esempio semplice ma potente di come sia possibile rappresentare oggetti tridimensionali su un piano bidimensionale. Comprendere questo concetto fondamentale apre le porte a un mondo di possibilità nel campo del disegno tecnico, dell'architettura, dell'ingegneria e del design. Speriamo che questo articolo ti abbia fornito una solida base per iniziare il tuo percorso di apprendimento e ti abbia ispirato ad esplorare ulteriormente le meraviglie della geometria descrittiva. Ricorda: la precisione e la chiarezza sono fondamentali per una corretta rappresentazione. Buono studio!