Problemi Con Le Frazioni Scuola Primaria Con Soluzioni

Le frazioni rappresentano un concetto fondamentale nella matematica elementare, e la loro comprensione è cruciale per il successo negli studi successivi. Tuttavia, molti bambini delle scuole primarie incontrano difficoltà nell'apprendimento delle frazioni. Questo articolo esplorerà le ragioni comuni di queste difficoltà, fornirà esempi concreti e offrirà soluzioni pratiche per aiutare i bambini a superare questi ostacoli.
Perché le Frazioni Sono Difficili?
Diversi fattori possono contribuire alle difficoltà che i bambini incontrano con le frazioni. Comprendere queste ragioni è il primo passo per affrontare il problema.
Rappresentazione Astratta
Una delle principali sfide è la natura astratta delle frazioni. I bambini sono abituati a manipolare oggetti interi, mentre le frazioni rappresentano parti di un intero. Questa differenza può essere difficile da concettualizzare. Ad esempio, capire che 1/2 di una torta è diversa da 1/2 di un biscotto richiede un certo livello di astrazione.
Comprensione del Concetto di Intero
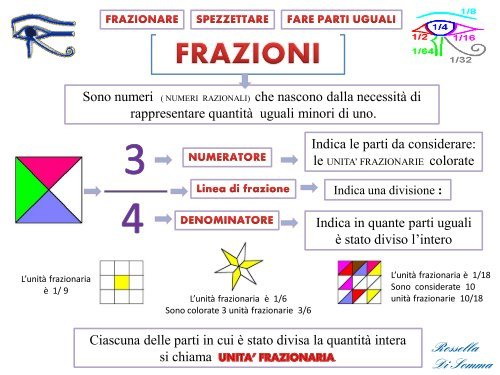
La comprensione del concetto di "intero" è essenziale per capire le frazioni. Se un bambino non comprende che una frazione rappresenta una parte di un intero definito, avrà difficoltà a capire il significato della frazione stessa. L'intero può essere un oggetto singolo (una pizza, una barretta di cioccolato) o un insieme di oggetti (un gruppo di caramelle, una scatola di pastelli).
Vocabolario e Simbologia Specifica
Le frazioni introducono un nuovo vocabolario e una nuova simbologia. I termini "numeratore," "denominatore," "frazione propria," "frazione impropria" e il simbolo "/" possono confondere i bambini. La comprensione di questi termini e simboli è fondamentale per la manipolazione e la risoluzione dei problemi con le frazioni.
Operazioni con le Frazioni
Le operazioni con le frazioni (addizione, sottrazione, moltiplicazione e divisione) richiedono regole specifiche che possono sembrare controintuitive rispetto alle operazioni con i numeri interi. Ad esempio, per sommare due frazioni, è necessario trovare un denominatore comune, un concetto che può essere difficile da afferrare per i bambini più piccoli.
Strategie per Superare le Difficoltà
Esistono diverse strategie che gli insegnanti e i genitori possono utilizzare per aiutare i bambini a superare le difficoltà con le frazioni. Queste strategie si concentrano sull'uso di materiali concreti, sulla visualizzazione e sulla connessione con il mondo reale.
Utilizzo di Materiali Manipolativi
L'uso di materiali manipolativi come blocchi frazionari, cerchi frazionari, regoli e frazioni di carta può rendere il concetto di frazione più tangibile e comprensibile. Questi materiali permettono ai bambini di visualizzare e manipolare le frazioni, facilitando la comprensione del loro significato e delle loro relazioni. Ad esempio, utilizzando i blocchi frazionari, un bambino può facilmente vedere che due blocchi da 1/4 equivalgono a un blocco da 1/2.
Rappresentazioni Visive
Le rappresentazioni visive, come diagrammi a torta, linee numeriche e rettangoli divisi, possono aiutare i bambini a visualizzare le frazioni e a confrontarle. Disegnare e colorare le frazioni può rendere il processo di apprendimento più coinvolgente e memorabile. Ad esempio, una linea numerica può essere utilizzata per confrontare 1/2, 1/4 e 3/4 e per visualizzare la loro posizione relativa.
Connessioni con il Mondo Reale
Collegare le frazioni al mondo reale può rendere il concetto più significativo e rilevante per i bambini. Esempi di situazioni quotidiane in cui le frazioni sono utilizzate includono la divisione di una pizza tra amici, la misurazione degli ingredienti in una ricetta, la lettura dell'ora (un quarto d'ora, mezz'ora) e la condivisione di giocattoli tra fratelli. Questi esempi concreti aiutano i bambini a capire che le frazioni non sono solo un concetto astratto, ma sono utilizzate nella vita di tutti i giorni.
Giochi ed Attività Interattive
L'apprendimento attraverso il gioco è un modo efficace per coinvolgere i bambini e rendere l'apprendimento più divertente. Esistono numerosi giochi e attività interattive che possono aiutare i bambini a praticare le frazioni, come giochi da tavolo, carte frazionarie e app educative. Questi giochi possono aiutare i bambini a sviluppare una comprensione più profonda delle frazioni mentre si divertono.
Focus sulla Comprensione Concettuale, Non sulla Memorizzazione Meccanica
È importante che i bambini comprendano il perché le frazioni funzionano in un determinato modo, piuttosto che semplicemente memorizzare le regole. Incoraggiare i bambini a spiegare il loro ragionamento e a giustificare le loro risposte può aiutarli a sviluppare una comprensione più profonda delle frazioni. Ad esempio, invece di dire semplicemente "per sommare le frazioni devi trovare un denominatore comune," spiegare perché è necessario fare questo può aiutare i bambini a capire il concetto.
Esempi Pratici e Soluzioni
Ecco alcuni esempi specifici di problemi comuni con le frazioni e le possibili soluzioni:
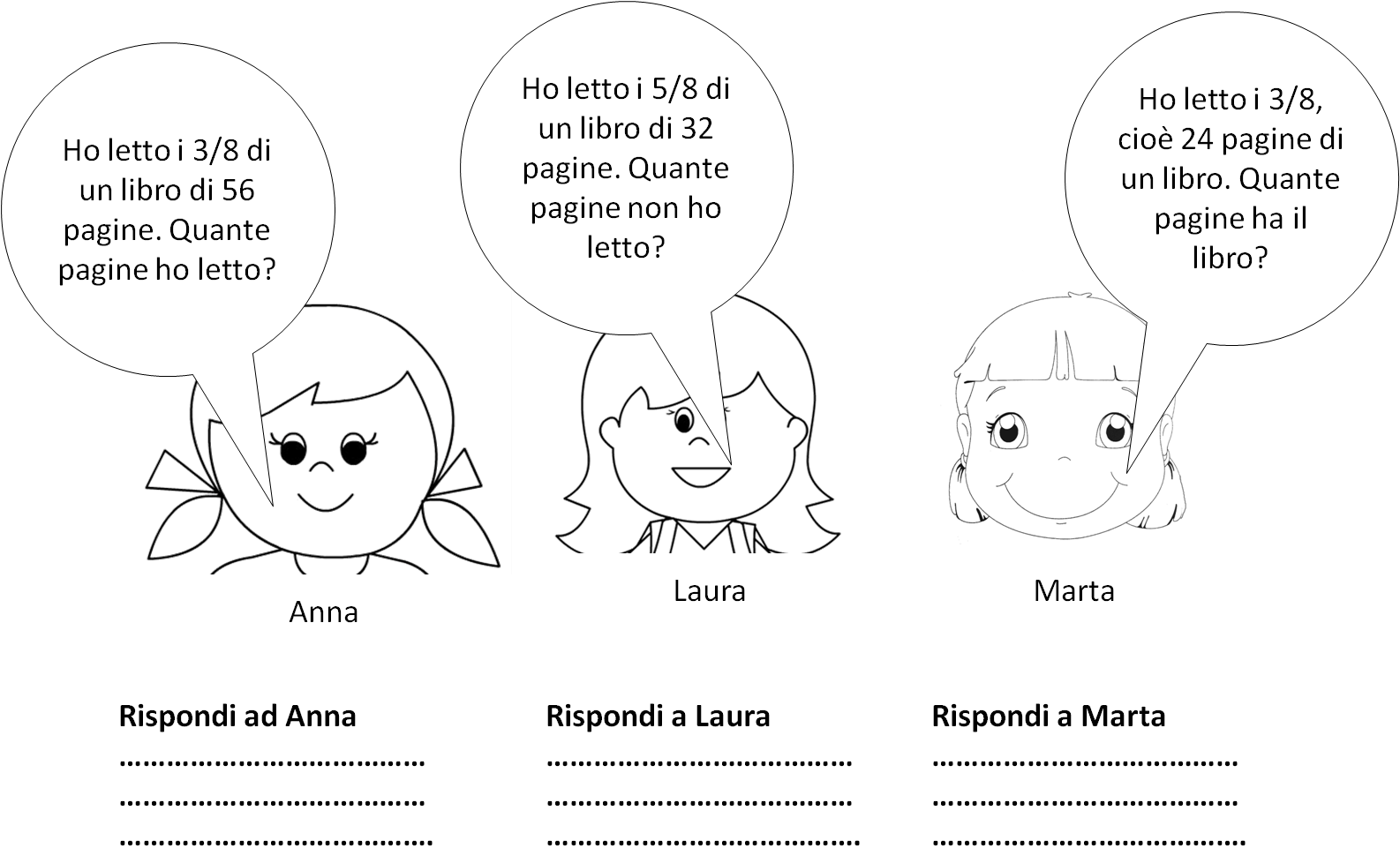
Problema: Confrontare Frazioni con Denominatori Diversi
Un bambino ha difficoltà a confrontare 1/3 e 1/4. Non riesce a capire quale frazione è più grande.
Soluzione: Utilizzare blocchi frazionari o diagrammi a torta. Mostrare visivamente che una parte di un intero diviso in tre parti è più grande di una parte dello stesso intero diviso in quattro parti. In alternativa, introdurre il concetto di denominatore comune. Trasformare 1/3 in 4/12 e 1/4 in 3/12. A questo punto, diventa evidente che 4/12 è maggiore di 3/12.
Problema: Sommare Frazioni con Denominatori Diversi
Un bambino non sa come sommare 1/2 e 1/4.
Soluzione: Utilizzare frazioni di carta. Mostrare che 1/2 è equivalente a 2/4. A questo punto, la somma diventa 2/4 + 1/4 = 3/4. In alternativa, spiegare il concetto di denominatore comune (in questo caso, 4). Trasformare 1/2 in 2/4 e quindi sommare 2/4 + 1/4 = 3/4.
Problema: Comprendere le Frazioni Improprie e i Numeri Misti
Un bambino ha difficoltà a capire cosa significa 5/4.
Soluzione: Utilizzare pizze o torte. Mostrare che 5/4 significa avere una pizza intera (4/4) e un quarto di un'altra pizza (1/4). Spiegare che 5/4 è una frazione impropria e che può essere espressa come un numero misto: 1 1/4.
Problema: Applicare le Frazioni a Problemi Pratici
Un bambino non riesce a risolvere problemi come "Se ho una torta e ne mangio 1/3, quanta torta mi rimane?".
Soluzione: Utilizzare oggetti reali (o disegni). Dividere la torta in tre parti uguali. Togliere una parte (1/3). Chiedere al bambino quante parti rimangono (2/3). Enfatizzare che l'intero è sempre rappresentato da 1 (o 3/3 in questo caso).
Utilizzo di Dati ed Esempi del Mondo Reale
Incorporare dati ed esempi del mondo reale può rendere l'apprendimento delle frazioni più interessante e significativo. Ad esempio:
- Ricette di Cucina: Utilizzare ricette per mostrare come le frazioni sono utilizzate per misurare gli ingredienti. Ad esempio, una ricetta potrebbe richiedere 1/2 tazza di farina, 1/4 cucchiaino di sale e 3/4 tazza di zucchero.
- Sport: Discutere le statistiche sportive che utilizzano le frazioni, come la percentuale di successo nei tiri liberi nel basket (ad esempio, un giocatore che realizza 3/4 dei suoi tiri liberi ha una percentuale di successo del 75%).
- Musica: Spiegare come le frazioni sono utilizzate in musica per rappresentare la durata delle note (ad esempio, una semibreve dura 4/4 di un battito, una minima dura 2/4 di un battito, una semiminima dura 1/4 di un battito).
- Costruzioni: Discutere come le frazioni sono utilizzate in edilizia per misurare i materiali da costruzione (ad esempio, un pezzo di legno potrebbe essere lungo 3 e 1/2 metri).
Questi esempi concreti aiutano i bambini a capire che le frazioni sono uno strumento utile e rilevante nella vita di tutti i giorni.
Conclusione
Le difficoltà con le frazioni sono comuni nella scuola primaria, ma con l'approccio giusto, i bambini possono superare questi ostacoli e sviluppare una solida comprensione di questo concetto fondamentale. L'uso di materiali manipolativi, rappresentazioni visive, connessioni con il mondo reale e giochi interattivi può rendere l'apprendimento delle frazioni più coinvolgente e significativo. È importante concentrarsi sulla comprensione concettuale piuttosto che sulla memorizzazione meccanica e fornire ai bambini l'opportunità di praticare le frazioni in contesti diversi. Incoraggiare la discussione e la spiegazione del ragionamento aiuta a sviluppare una comprensione più profonda e duratura. Se i bambini ricevono il supporto e le risorse di cui hanno bisogno, possono affrontare le frazioni con sicurezza e successo. Incoraggiamo genitori ed educatori a implementare queste strategie per supportare gli studenti nel loro percorso di apprendimento delle frazioni.