Primo Criterio Di Congruenza Dei Triangoli

Ti sei mai chiesto come fanno i geometri a sapere se due triangoli sono esattamente identici senza doverli sovrapporre fisicamente? La risposta si trova spesso in un principio fondamentale della geometria: il primo criterio di congruenza dei triangoli. Immagina di dover costruire un ponte. La precisione è fondamentale, e sapere che le strutture di supporto sono esattamente uguali è cruciale per la stabilità. Questo criterio ci fornisce proprio questa certezza, un metodo infallibile per verificare la congruenza.

Questo articolo è pensato per te, che magari ti sei imbattuto in questo concetto a scuola o semplicemente sei curioso di saperne di più. Cercheremo di spiegarlo in modo chiaro, pratico e senza inutili complicazioni.

Cosa significa congruenza?

Prima di addentrarci nel primo criterio, chiariamo cosa intendiamo per congruenza. Due figure geometriche sono congruenti se hanno esattamente la stessa forma e le stesse dimensioni. In altre parole, puoi immaginarle come due ritagli di carta identici. Se prendessi uno dei due e lo sovrapponessi all'altro, combacerebbero perfettamente. Questa definizione è cruciale per capire l'importanza dei criteri di congruenza.

Nel caso specifico dei triangoli, la congruenza implica che tutti e tre i lati e tutti e tre gli angoli corrispondenti siano uguali.

Il Primo Criterio: Lati e Angolo Compreso

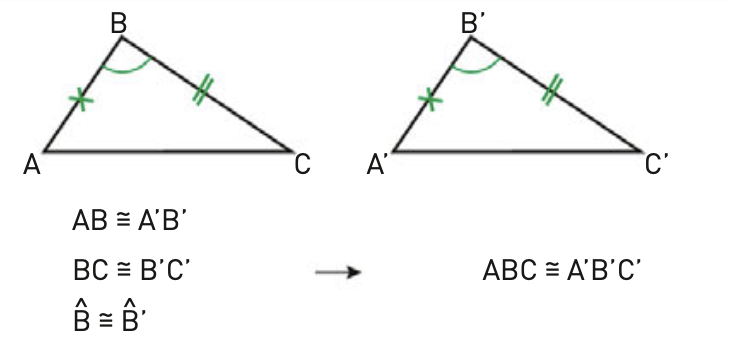
Eccoci al cuore dell'argomento. Il primo criterio di congruenza (detto anche criterio Lato-Angolo-Lato o LAL) afferma che:

Se due triangoli hanno due lati rispettivamente congruenti e l'angolo tra essi compreso congruente, allora i due triangoli sono congruenti.

Cerchiamo di scomporre questa affermazione:

* **Due lati rispettivamente congruenti:** Significa che c'è una coppia di lati nel primo triangolo che ha la stessa lunghezza di una coppia di lati nel secondo triangolo. * **Angolo tra essi compreso congruente:** Significa che l'angolo formato dai due lati congruenti nel primo triangolo è esattamente uguale all'angolo formato dai due lati congruenti nel secondo triangolo.

Se queste condizioni sono soddisfatte, allora possiamo concludere, senza ombra di dubbio, che i due triangoli sono identici e congruenti.

Un Esempio Pratico

Immagina due triangoli, ABC e DEF. Supponiamo che:

* AB = DE (il lato AB del triangolo ABC è uguale al lato DE del triangolo DEF) * AC = DF (il lato AC del triangolo ABC è uguale al lato DF del triangolo DEF) * L'angolo BAC = l'angolo EDF (l'angolo formato dai lati AB e AC è uguale all'angolo formato dai lati DE e DF)

In base al primo criterio di congruenza, possiamo affermare con certezza che il triangolo ABC è congruente al triangolo DEF.

Perché Funziona? Una Dimostrazione Intuitiva

Potresti chiederti: perché questo criterio è valido? Proviamo a visualizzarlo.

Immagina di avere due bastoncini di lunghezza fissa (i due lati congruenti) e di unirli ad una estremità formando un angolo (l'angolo compreso congruente). La lunghezza dei bastoncini e l'ampiezza dell'angolo sono le stesse per entrambi i triangoli. Se ora colleghi le estremità libere dei due bastoncini per formare il terzo lato del triangolo, la lunghezza di questo lato sarà univocamente determinata. Non ci sono altre possibilità! Poiché tutti e tre i lati sono uguali, i triangoli sono congruenti.

Come Applicare il Primo Criterio

L'applicazione del primo criterio è relativamente semplice. Ecco alcuni passaggi:

1. Identifica i triangoli: Assicurati di avere due triangoli distinti da confrontare. 2. Verifica i lati congruenti: Cerca due coppie di lati che abbiano la stessa lunghezza. Questo può essere dato direttamente nel problema o dedotto da altre informazioni. 3. Verifica l'angolo compreso congruente: Assicurati che l'angolo formato dai due lati congruenti sia lo stesso in entrambi i triangoli. Anche in questo caso, potrebbe essere dato direttamente o dedotto. 4. Concludi: Se tutte e tre le condizioni sono soddisfatte, allora puoi affermare con sicurezza che i due triangoli sono congruenti.

Esempi di Applicazione

Esempio 1:

Considera due triangoli, PQR e STU, tali che PQ = ST = 5 cm, PR = SU = 7 cm e l'angolo QPR = l'angolo TSU = 60°. Possiamo concludere che i triangoli PQR e STU sono congruenti per il primo criterio di congruenza.

Esempio 2:

Immagina di avere un triangolo isoscele ABC con base BC. Traccia l'altezza AH relativa alla base. L'altezza divide il triangolo ABC in due triangoli rettangoli, ABH e ACH. Abbiamo:

* AH = AH (lato in comune) * AB = AC (perché ABC è isoscele) * L'angolo AHB = l'angolo AHC = 90° (perché AH è un'altezza)

Quindi, i triangoli ABH e ACH sono congruenti per il primo criterio. Questo ci permette di dimostrare che l'altezza in un triangolo isoscele è anche mediana e bisettrice.

L'Importanza del Primo Criterio

Il primo criterio di congruenza è un mattone fondamentale nella geometria. Non solo ti permette di dimostrare la congruenza di triangoli, ma è anche alla base di molte altre dimostrazioni e teoremi. È uno strumento essenziale per risolvere problemi geometrici e per comprendere le relazioni tra diverse figure.

Ad esempio, è utilizzato frequentemente nella dimostrazione di proprietà di figure più complesse, come parallelogrammi, trapezi e poligoni regolari. La sua applicazione permette di semplificare l'analisi di queste figure, scomponendole in triangoli più semplici e gestibili.

Errori Comuni da Evitare

Anche se il primo criterio sembra semplice, è facile commettere errori se non si presta attenzione. Ecco alcuni errori comuni da evitare:

* Confondere l'ordine: Ricorda, è *lato-angolo-lato*. Non puoi usare questo criterio se hai due lati congruenti e un angolo congruente *non* compreso tra quei lati. * Assumere la congruenza senza prove: Non dare per scontato che i lati o gli angoli siano congruenti solo perché sembrano uguali nel disegno. Devi avere una prova esplicita (data nel problema o dedotta da altre informazioni). * Non verificare tutte le condizioni: Assicurati di aver verificato la congruenza di entrambi i lati e dell'angolo compreso. Mancare una sola condizione invalida l'applicazione del criterio.

Conclusione

Il primo criterio di congruenza dei triangoli è uno strumento potente e versatile. Con una comprensione chiara dei suoi principi e un po' di pratica, potrai utilizzarlo con sicurezza per risolvere problemi geometrici e per approfondire la tua conoscenza della geometria. Ricorda: lato-angolo-lato! La precisione è fondamentale, e questo criterio ti offre la certezza che cerchi nella geometria.

Spero che questo articolo ti sia stato utile. Ora, prova ad applicare il primo criterio a diversi problemi e vedrai come la geometria può diventare più chiara e intuitiva!