Potenza Con Stessa Base E Stesso Esponente

Comprendere le potenze è fondamentale in matematica e in molte discipline scientifiche. Una situazione particolare, ma molto interessante, si verifica quando abbiamo a che fare con potenze aventi la stessa base e lo stesso esponente. Sebbene possa sembrare un caso limitato, analizzarlo a fondo rivela principi importanti e applicazioni pratiche inaspettate.

Potenze con Base ed Esponente Uguali: Concetti Chiave

Definizione Fondamentale

Una potenza è un'espressione matematica che indica la moltiplicazione di un numero (la base) per se stesso un certo numero di volte (l'esponente). Formalmente, aⁿ significa moltiplicare a per se stesso n volte. Quando la base a è uguale all'esponente n, otteniamo una potenza nella forma a^a. Questa semplice condizione apre le porte a considerazioni più approfondite.

Comportamento Crescente

Una delle caratteristiche più evidenti delle potenze a^a è la loro crescita estremamente rapida. Anche con valori piccoli di a, il risultato cresce in modo vertiginoso. Ad esempio:

2² = 4
3³ = 27
4⁴ = 256
5⁵ = 3125

Questa crescita esponenziale ha implicazioni significative in vari campi, dall'informatica alla biologia.

Rappresentazione Grafica

Se rappresentiamo graficamente la funzione f(x) = x^x, otteniamo una curva che cresce esponenzialmente per x > 1. È importante notare che la funzione non è definita per x = 0 nel dominio dei numeri reali, poiché 0⁰ è una forma indeterminata (anche se in alcuni contesti può essere definita come 1). Per x < 0, la funzione è definita solo per valori interi negativi pari di x, dando risultati positivi. I valori negativi dispari di x danno risultati negativi.

Operazioni e Manipolazioni

Sebbene le potenze con base ed esponente uguali non abbiano proprietà algebriche specifiche che le distinguano da altre potenze, è cruciale ricordare le regole generali delle potenze. Ad esempio:

(a^a)^b = a^a*b (Potenza di una potenza)
a^a * a^a = a^2a (Prodotto di potenze con la stessa base)

È fondamentale non confondere a^a * a^a con (a*a)^a*a = (a²)^a², che sono espressioni completamente diverse.

Considerazioni sui Numeri Complessi

L'analisi delle potenze a^a si complica quando si considerano i numeri complessi. La funzione z^z, dove z è un numero complesso, è una funzione multivalore a causa della natura del logaritmo complesso. Questo significa che per ogni valore di z, ci sono infiniti possibili valori per z^z. Questo è legato alla periodicità della funzione esponenziale complessa (e^ix ha periodo 2π). Esplorare le proprietà di z^z nel piano complesso richiede una conoscenza approfondita dell'analisi complessa.

Esempi Pratici e Applicazioni

Informatica: Complessità Algoritmica

La crescita esponenziale delle potenze a^a trova un riscontro diretto nell'analisi della complessità algoritmica. Alcuni algoritmi, sebbene rari, possono avere una complessità temporale dell'ordine di nⁿ, dove n rappresenta la dimensione dell'input. Questo significa che il tempo di esecuzione dell'algoritmo cresce in modo catastrofico all'aumentare di n, rendendolo impraticabile per input anche di modeste dimensioni. Fortunatamente, algoritmi con tale complessità sono rarissimi e generalmente evitati nella pratica.

Biologia: Crescita Popolazionale Teorica

In modelli semplificati di crescita popolazionale, si può immaginare una situazione in cui ogni individuo si riproduce producendo un numero di figli pari al numero totale di individui presenti. Sebbene irrealistico, questo scenario porta a una crescita descritta da una potenza del tipo a^a, dove a rappresenta la popolazione iniziale. Chiaramente, in contesti reali, fattori limitanti come la disponibilità di risorse e la competizione interspecifica impediscono una crescita così esplosiva.

Matematica Ricreativa: Giochi e Puzzle

Le potenze a^a possono comparire in giochi e puzzle matematici. Ad esempio, si potrebbe chiedere di trovare il più piccolo intero positivo n tale che nⁿ sia maggiore di un certo numero dato. Questi problemi stimolano il ragionamento logico e la comprensione delle proprietà delle potenze.

Analisi dei Dati: Crescita di Internet

Anche se non esattamente nella forma a^a, la crescita di Internet e dei social media presenta analogie con la crescita esponenziale. Il numero di utenti, il traffico dati e la capacità di calcolo tendono a crescere in modo rapido, anche se non indefinitamente. Analizzare questi dati e modellarne la crescita richiede l'uso di funzioni esponenziali e logaritmiche, che sono strettamente legate al concetto di potenza.

Limitazioni e Considerazioni Avanzate

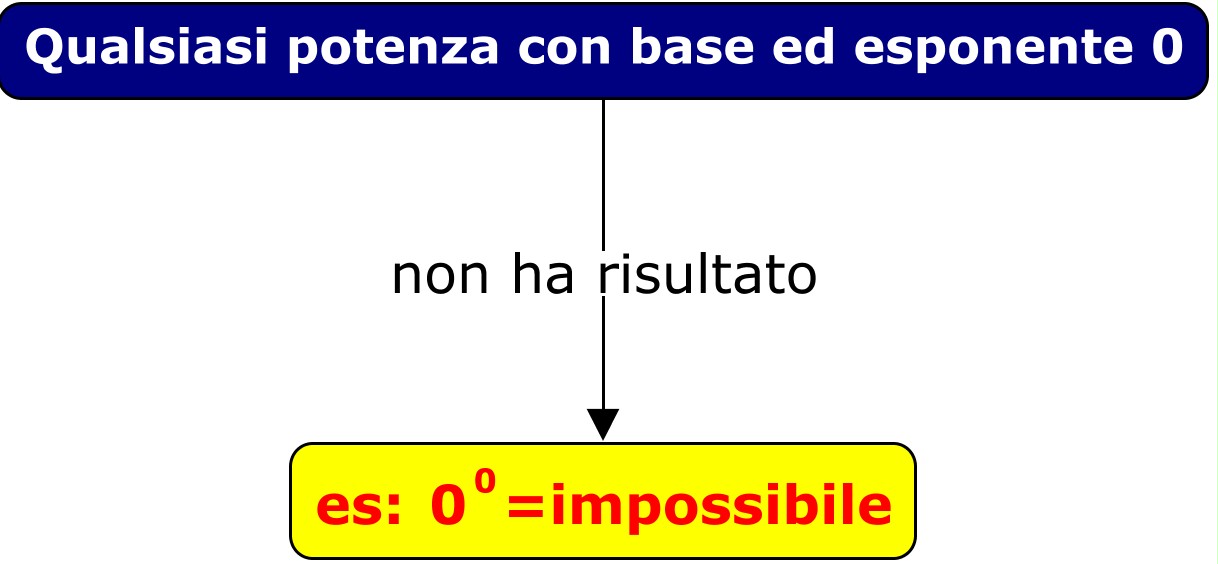
Forme Indeterminate: 0⁰

Come accennato, la forma 0⁰ è una forma indeterminata. Questo significa che il suo valore non può essere determinato semplicemente sostituendo 0 nell'espressione. Il valore di 0⁰ dipende dal contesto specifico. In alcuni contesti, come nella teoria degli insiemi o nel calcolo combinatorio, è conveniente definire 0⁰ = 1. In altri contesti, come nel calcolo infinitesimale, 0⁰ è considerata indefinita.

Generalizzazioni: Iterazione di Funzioni

Il concetto di a^a può essere generalizzato all'iterazione di funzioni. Ad esempio, si può definire una funzione f(x) = x^x e iterarla più volte: f(f(x)), f(f(f(x))), e così via. Questo porta a strutture matematiche complesse e interessanti, studiate nell'ambito della dinamica non lineare e della teoria del caos. Un esempio ben noto è la torre di potenze, come 2^{2^2²}, dove l'elevamento a potenza viene applicato ripetutamente.

Approssimazioni Asintotiche

Per valori grandi di a, calcolare a^a direttamente può diventare computazionalmente costoso. In questi casi, si possono utilizzare approssimazioni asintotiche basate sulla formula di Stirling o altre tecniche di analisi asintotica. Queste approssimazioni forniscono stime accurate del valore di a^a senza la necessità di calcolare l'intera espressione.

Conclusioni

Le potenze con la stessa base e lo stesso esponente, pur apparendo come un caso specifico, rappresentano un punto di partenza interessante per esplorare concetti fondamentali della matematica e le loro applicazioni in diversi campi. Dalla rapida crescita esponenziale alla complessità algoritmica, passando per le forme indeterminate e le generalizzazioni, a^a ci invita a riflettere sulla potenza del concetto di potenza e sulla sua onnipresenza nel mondo che ci circonda. Continuare ad esplorare le proprietà e le applicazioni di queste potenze può portare a nuove scoperte e a una comprensione più profonda del linguaggio della matematica.