Piramide Retta Con Base Triangolo Isoscele

Immagina di tenere tra le mani un cristallo sfaccettato, una piccola piramide. Ma questa non è una piramide qualsiasi. La sua base è un triangolo isoscele, due lati uguali che le conferiscono un equilibrio particolare. In questo articolo, esploreremo in dettaglio le caratteristiche, le proprietà e i calcoli relativi a questa affascinante forma geometrica: la piramide retta con base triangolo isoscele. Che tu sia uno studente alle prese con la geometria solida, un appassionato di matematica o semplicemente curioso di saperne di più, questa guida ti fornirà una comprensione chiara e completa.

Cos'è una Piramide Retta con Base Triangolo Isoscele?

Per capire a fondo di cosa stiamo parlando, definiamo i termini chiave:

• Piramide: Un solido geometrico formato collegando tutti i punti di un poligono (la base) a un singolo punto, chiamato vertice.
• Piramide Retta: Una piramide in cui l'altezza (la linea perpendicolare dalla base al vertice) interseca la base nel suo centro geometrico. Nel nostro caso, l'altezza incontrerà la base triangolare isoscele nel punto di intersezione delle mediane, altezze e bisettrici relative alla base.
• Triangolo Isoscele: Un triangolo con almeno due lati di uguale lunghezza. Questo implica anche che gli angoli opposti a questi lati uguali siano anch'essi uguali.

Quindi, una piramide retta con base triangolo isoscele è una figura solida in cui un triangolo isoscele costituisce la base e il vertice della piramide è posizionato direttamente sopra il centro di questa base, in modo che la linea che li connette (l'altezza) sia perpendicolare alla base stessa. Questa definizione ci permette di visualizzare la forma e capire la sua simmetria.

Caratteristiche Chiave

Le caratteristiche principali di questa piramide derivano direttamente dalle proprietà del triangolo isoscele e dalla condizione di piramide retta:

• Base: Un triangolo isoscele con due lati uguali (chiamiamoli l) e un lato diverso (la base del triangolo, che chiameremo b).
• Altezza della Piramide (h): La distanza perpendicolare dal vertice della piramide al piano della base.
• Altezza del Triangolo Isoscele (h_t): La distanza perpendicolare dalla base del triangolo al vertice opposto. Questa altezza divide il triangolo isoscele in due triangoli rettangoli congruenti.
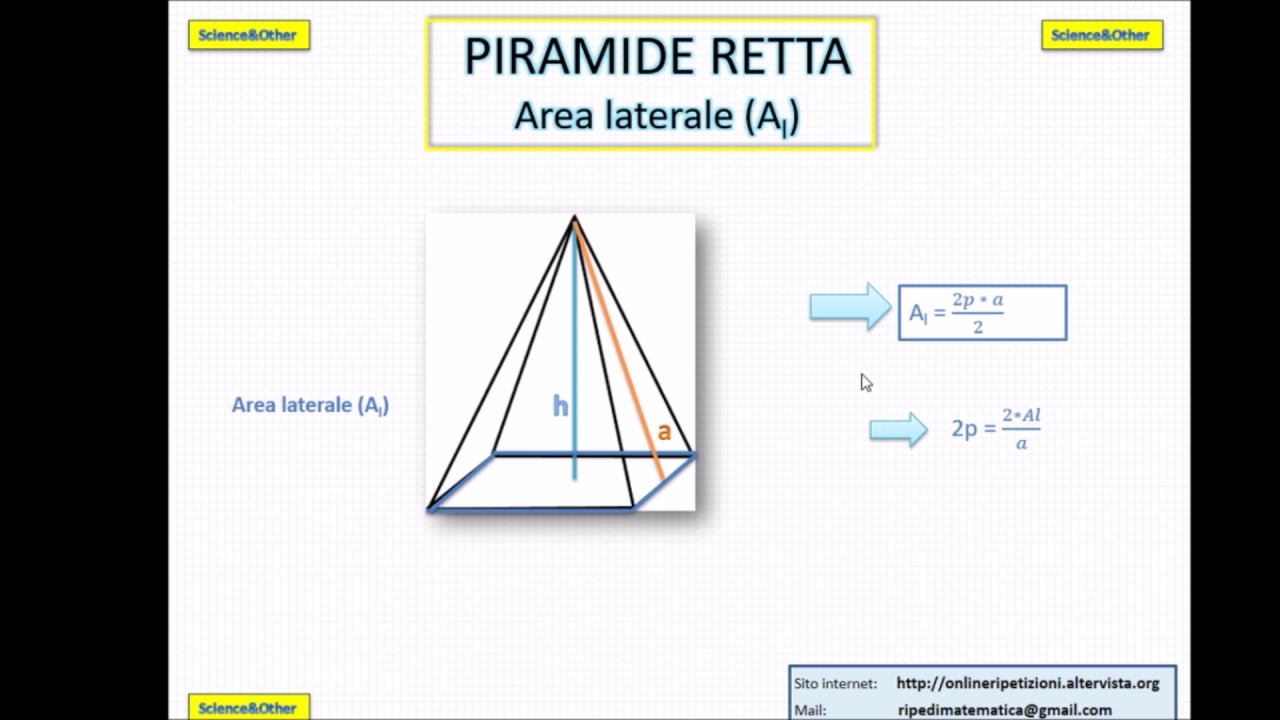
• Apotema della Piramide (a): L'altezza di una faccia laterale della piramide, misurata dal vertice della piramide al lato della base triangolare. Ci saranno tre apotemi differenti, uno per ogni faccia laterale. Due di questi apotemi saranno uguali perché i due lati uguali del triangolo isoscele produrranno due facce laterali congruenti.
• Facce Laterali: Tre triangoli che si incontrano al vertice della piramide. Due di questi triangoli saranno congruenti a causa dei lati uguali del triangolo isoscele di base.

Calcoli Importanti: Area e Volume

Comprendere come calcolare l'area e il volume di una piramide retta con base triangolo isoscele è fondamentale. Vediamo nel dettaglio le formule e i passaggi necessari:

Area Totale

L'area totale della piramide è la somma dell'area della base (il triangolo isoscele) e l'area delle tre facce laterali (triangoli).

1. Area della Base (A_b): L'area di un triangolo isoscele è data da:
   A_b = (1/2) * b * h_t
   Dove b è la lunghezza della base del triangolo isoscele e h_t è la sua altezza. Se non conosciamo direttamente l'altezza, possiamo calcolarla usando il teorema di Pitagora, sapendo che l'altezza divide il triangolo isoscele in due triangoli rettangoli:
   h_t = √(l² - (b/2)²)
   Dove l è la lunghezza dei lati uguali del triangolo isoscele.
2. Area Laterale (A_l): L'area laterale è la somma delle aree delle tre facce triangolari. Come menzionato prima, due di queste facce avranno la stessa area. Calcoliamo quindi l'area di una delle facce uguali e l'area della terza faccia:
   • Area di una faccia laterale uguale: (1/2) * l * a_l, dove a_l è l'apotema relativa al lato l.
   • Area della faccia laterale disuguale: (1/2) * b * a_b, dove a_b è l'apotema relativa alla base b.
   A_l = (l * a_l) + (1/2) * b * a_b
3. Area Totale (A_t): La somma dell'area della base e dell'area laterale:
   A_t = A_b + A_l
   A_t = (1/2) * b * h_t + (l * a_l) + (1/2) * b * a_b

Per calcolare gli apotemi (a_l e a_b), avremo bisogno dell'altezza della piramide (h) e delle distanze dal centro della base ai lati del triangolo isoscele. Queste distanze possono essere calcolate usando le proprietà del triangolo isoscele e il teorema di Pitagora. Per esempio, se consideriamo il triangolo rettangolo formato dall'altezza della piramide (h), dalla distanza dal centro della base al lato *l* (che chiameremo *d_l*) e dall'apotema *a_l*, possiamo scrivere: *a_l* = √(h² + *d_l*²). Analogamente, *a_b* = √(h² + *d_b*²), dove *d_b* è la distanza dal centro della base alla base *b* del triangolo isoscele.

Volume

Il volume di una piramide è dato da:

Dove A_b è l'area della base (il triangolo isoscele) e h è l'altezza della piramide. Sostituendo l'espressione per l'area del triangolo isoscele, otteniamo:

Esempio Pratico

Consideriamo una piramide retta con base triangolo isoscele dove i lati uguali del triangolo (l) misurano 5 cm, la base del triangolo (b) misura 6 cm e l'altezza della piramide (h) è di 4 cm.

1. Calcolo dell'altezza del triangolo isoscele (h_t):
   h_t = √(5² - (6/2)²) = √(25 - 9) = √16 = 4 cm
2. Calcolo dell'area della base (A_b):
   A_b = (1/2) * 6 * 4 = 12 cm²
3. Calcolo del volume (V):
   V = (1/3) * 12 * 4 = 16 cm³

Calcolare gli apotemi e l'area totale è un po' più complesso e richiederebbe calcolare le distanze *d_l* e *d_b* dal centro della base ai lati del triangolo, cosa che non è immediata e dipende dalla posizione del centro rispetto al triangolo isoscele. In generale, il centro della base di una piramide retta è il punto di intersezione delle mediane del triangolo isoscele. Trovare queste distanze richiede un po' più di trigonometria e geometria analitica, ma il principio rimane lo stesso: utilizzare il teorema di Pitagora per calcolare gli apotemi e poi sommare le aree delle facce laterali.

Applicazioni Reali

Anche se può sembrare un concetto puramente teorico, la piramide retta con base triangolo isoscele trova applicazioni in diversi campi:

• Architettura: Elementi decorativi, tetti di piccole strutture, design di facciate.
• Ingegneria: Progettazione di strutture di supporto, analisi di carichi e stabilità.
• Cristallografia: Studio delle forme cristalline di alcuni minerali.
• Design: Creazione di oggetti tridimensionali, packaging, gioielleria.

Conclusione

La piramide retta con base triangolo isoscele è una figura geometrica affascinante che combina le proprietà del triangolo isoscele e della piramide retta. Comprendere le sue caratteristiche, come calcolare la sua area e il suo volume, e conoscere le sue applicazioni pratiche ci permette di apprezzare la bellezza e l'utilità della geometria. Spero che questa guida ti abbia fornito una solida base per approfondire ulteriormente questo argomento e che tu possa utilizzare queste conoscenze per risolvere problemi e creare nuove soluzioni. Continua ad esplorare il mondo della geometria!