Piano Cartesiano Prima X O Y

Il piano cartesiano, un concetto fondamentale della matematica e della geometria analitica, offre un metodo potente per rappresentare graficamente equazioni e relazioni, e per analizzare dati in uno spazio bidimensionale. È uno strumento essenziale per la comprensione di molte discipline scientifiche e ingegneristiche.
Fondamenti del Piano Cartesiano
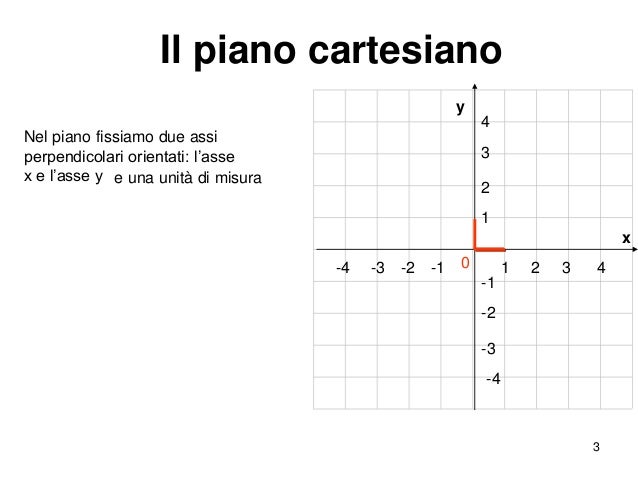
Il piano cartesiano è definito da due rette perpendicolari, chiamate assi cartesiani. L'asse orizzontale è denominato asse delle ascisse, o asse X, mentre l'asse verticale è denominato asse delle ordinate, o asse Y. Il punto in cui i due assi si intersecano è chiamato origine, ed è rappresentato dalle coordinate (0, 0).
Coordinate di un Punto
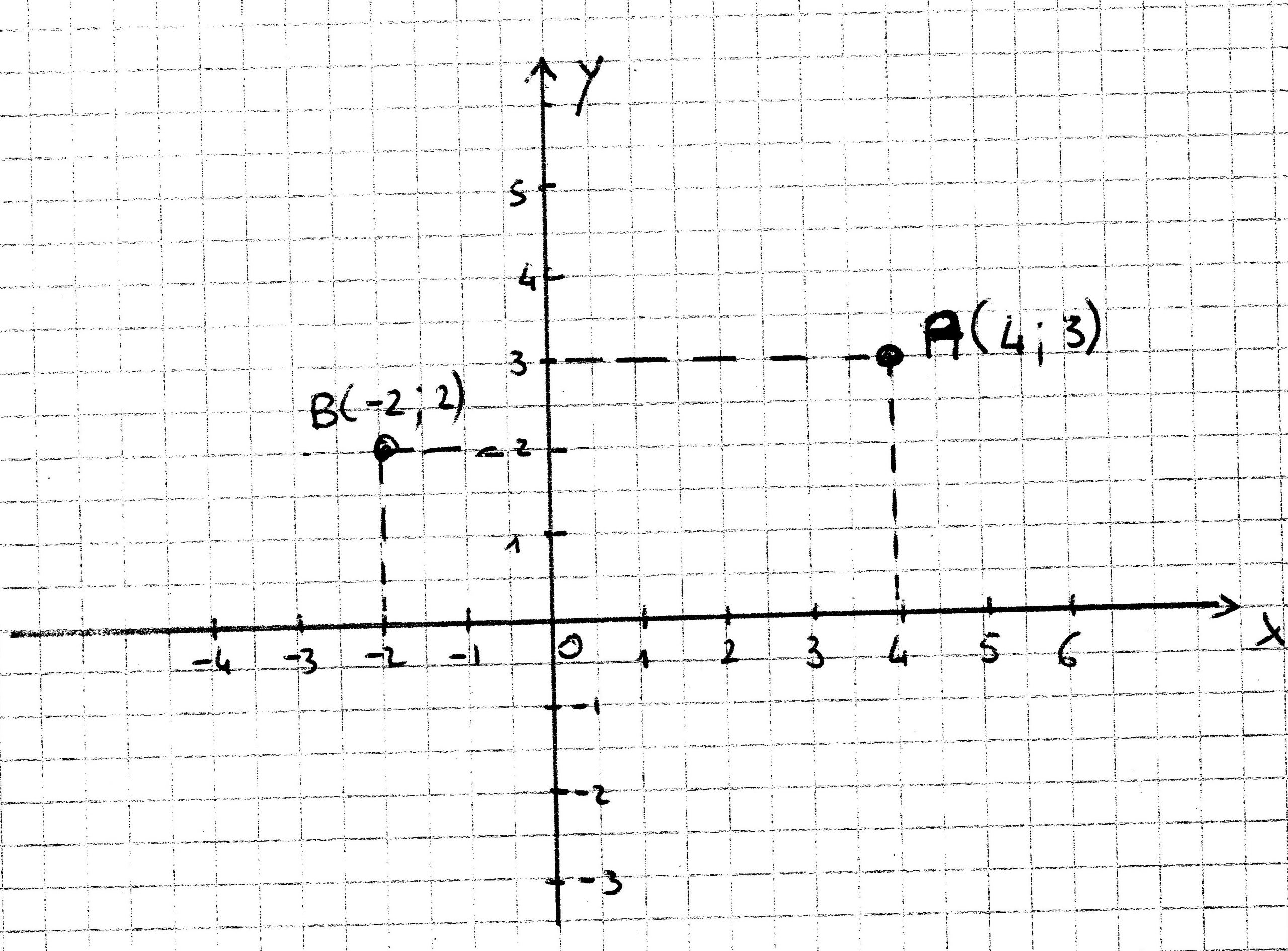
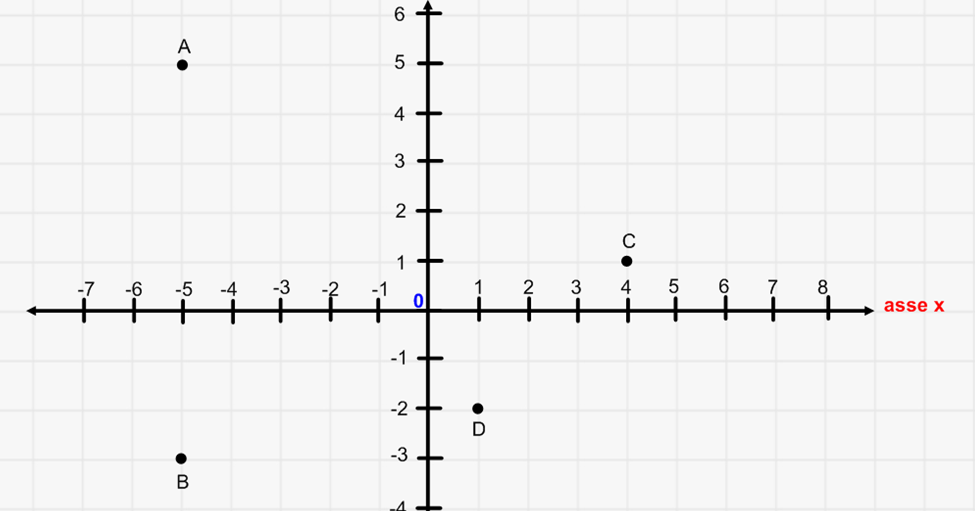
Ogni punto nel piano cartesiano è identificato da una coppia ordinata di numeri, chiamate coordinate. La prima coordinata, x, rappresenta la distanza orizzontale del punto dall'asse Y, mentre la seconda coordinata, y, rappresenta la distanza verticale del punto dall'asse X. Ad esempio, il punto (3, 2) si trova a 3 unità a destra dell'asse Y e a 2 unità sopra l'asse X.
Le coordinate sono scritte all'interno di parentesi tonde e separate da una virgola, seguendo la convenzione (x, y). L'ordine è fondamentale; (3, 2) è un punto diverso da (2, 3).
I Quadranti
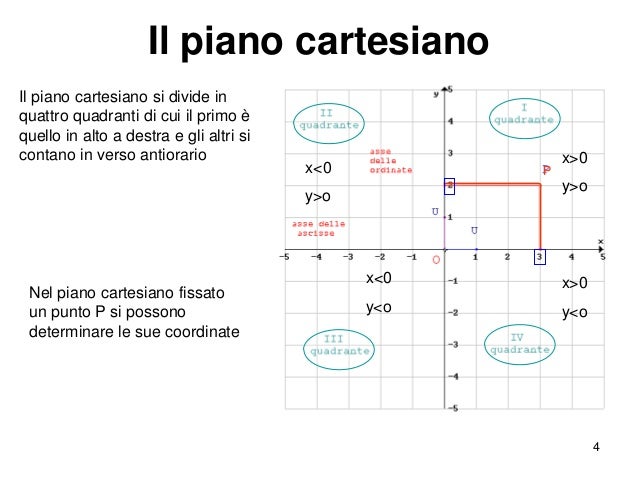
Gli assi cartesiani dividono il piano in quattro regioni chiamate quadranti:
- Primo quadrante: x > 0, y > 0 (entrambe le coordinate positive)
- Secondo quadrante: x < 0, y > 0 (ascissa negativa, ordinata positiva)
- Terzo quadrante: x < 0, y < 0 (entrambe le coordinate negative)
- Quarto quadrante: x > 0, y < 0 (ascissa positiva, ordinata negativa)
La conoscenza del quadrante in cui si trova un punto fornisce informazioni preliminari sul segno delle sue coordinate.
Applicazioni del Piano Cartesiano
Il piano cartesiano trova innumerevoli applicazioni in vari campi. Eccone alcuni esempi:
Geometria Analitica
In geometria analitica, il piano cartesiano permette di rappresentare figure geometriche (rette, curve, poligoni, ecc.) tramite equazioni algebriche. Ad esempio, una retta può essere rappresentata dall'equazione y = mx + q, dove m è il coefficiente angolare (la pendenza) e q è l'intercetta (il punto in cui la retta interseca l'asse Y).
La possibilità di associare equazioni a figure geometriche permette di risolvere problemi geometrici usando strumenti algebrici e viceversa.
Grafici di Funzioni
Il piano cartesiano è essenziale per visualizzare il grafico di una funzione. Se una funzione è definita come y = f(x), dove x è la variabile indipendente e y è la variabile dipendente, il grafico della funzione è l'insieme di tutti i punti (x, f(x)) nel piano cartesiano. Questo permette di visualizzare il comportamento della funzione, come la sua crescita, decrescita, punti di massimo e minimo, e periodicità.
Ad esempio, il grafico della funzione y = x2 è una parabola con il vertice nell'origine.
Analisi dei Dati
Nel campo dell'analisi dei dati, il piano cartesiano è utilizzato per visualizzare relazioni tra due variabili. Ad esempio, si possono rappresentare dati relativi al peso e all'altezza di un gruppo di persone, con il peso sull'asse X e l'altezza sull'asse Y. La visualizzazione dei dati nel piano cartesiano permette di identificare pattern, correlazioni e outlier.
Un diagramma di dispersione (scatter plot) è un esempio comune di utilizzo del piano cartesiano per l'analisi dei dati. Permette di visualizzare la distribuzione dei dati e di valutare la presenza di una correlazione tra le variabili.
Cartografia e Sistemi di Posizionamento Globale (GPS)
La cartografia utilizza sistemi di coordinate per rappresentare la superficie terrestre su una mappa. Sebbene la superficie terrestre sia tridimensionale, le mappe sono spesso bidimensionali e si basano su proiezioni che trasformano le coordinate geografiche (latitudine e longitudine) in coordinate piane, utilizzabili in un sistema cartesiano.
I sistemi di posizionamento globale (GPS) utilizzano satelliti per determinare la posizione di un ricevitore sulla superficie terrestre. Le coordinate GPS sono espresse in termini di latitudine e longitudine, che possono poi essere convertite in coordinate piane utilizzando proiezioni cartografiche basate sul piano cartesiano.
Videogiochi e Grafica Computerizzata
Nei videogiochi e nella grafica computerizzata, il piano cartesiano è utilizzato per definire la posizione e il movimento degli oggetti sullo schermo. Un oggetto può essere rappresentato come un insieme di punti (vertici) le cui coordinate sono definite nel piano cartesiano. Le trasformazioni geometriche (rotazione, traslazione, scalatura) possono essere implementate tramite operazioni matematiche sulle coordinate dei vertici.
Ad esempio, per spostare un oggetto di una certa distanza, si aggiungono le corrispondenti coordinate di traslazione alle coordinate di tutti i suoi vertici.
Limitazioni e Considerazioni
Nonostante la sua utilità, il piano cartesiano ha delle limitazioni. Principalmente, esso rappresenta solo uno spazio bidimensionale. Per rappresentare oggetti e fenomeni tridimensionali, è necessario estendere il concetto a uno spazio cartesiano tridimensionale, con l'aggiunta di un terzo asse, l'asse Z. Tuttavia, molti concetti e tecniche utilizzati nel piano cartesiano bidimensionale si estendono naturalmente allo spazio tridimensionale.
Inoltre, la scelta dell'unità di misura sugli assi può influenzare la visualizzazione dei dati. È importante scegliere un'unità di misura appropriata per evitare distorsioni e per facilitare l'interpretazione dei risultati.
Conclusioni
Il piano cartesiano è uno strumento fondamentale per la matematica, la scienza e l'ingegneria. La sua capacità di rappresentare graficamente equazioni e relazioni, di analizzare dati e di modellare fenomeni fisici lo rende uno strumento indispensabile per studenti, ricercatori e professionisti. Comprendere i principi del piano cartesiano è il primo passo verso la comprensione di concetti più avanzati in matematica e nelle sue applicazioni.
Invitiamo tutti a esplorare le diverse applicazioni del piano cartesiano e a sperimentare con la rappresentazione di funzioni e dati. La pratica e l'esplorazione sono la chiave per padroneggiare questo importante strumento.