Periodo E Antiperiodo Di Un Numero Decimale

Ti sei mai chiesto perché alcuni numeri decimali sembrano non finire mai, ripetendo all'infinito certe cifre? Capita a tutti di trovarsi di fronte a un numero come 3,3333... o 1,272727... e sentirsi un po' confusi. Non preoccuparti, non sei solo! Comprendere il periodo e l'antiperiodo di un numero decimale è più semplice di quanto sembri, e ti aprirà le porte a una migliore comprensione dei numeri razionali e delle frazioni.

In questo articolo, esploreremo insieme questi concetti, rendendoli chiari e accessibili. Dimentica i libri di matematica pieni di formule incomprensibili! Useremo esempi pratici e un linguaggio semplice per aiutarti a padroneggiare l'argomento. Che tu sia uno studente alle prese con le frazioni, un genitore che aiuta i propri figli con i compiti, o semplicemente una persona curiosa, questo articolo fa per te.

Cosa sono i Numeri Decimali? Un Ripasso Veloce

Prima di tuffarci nel periodo e nell'antiperiodo, facciamo un breve ripasso dei numeri decimali. Un numero decimale è un numero che ha una parte intera (a sinistra della virgola) e una parte frazionaria (a destra della virgola) separata da una virgola. Ad esempio, in 3,14, 3 è la parte intera e 14 è la parte frazionaria.

Esistono diversi tipi di numeri decimali:

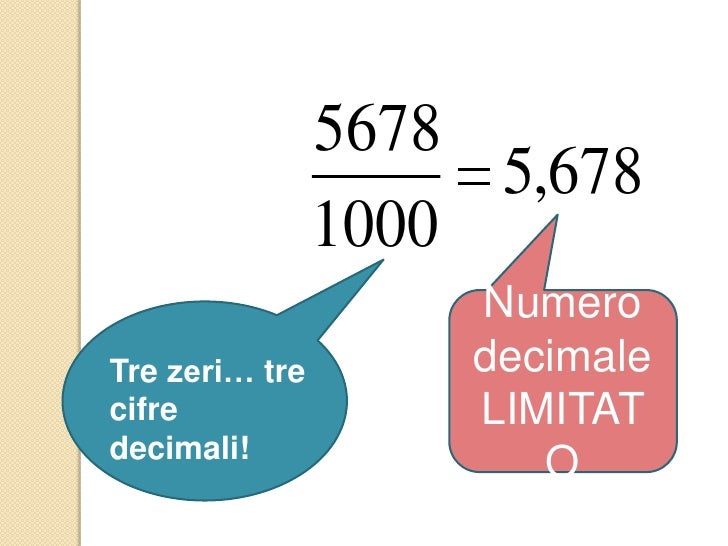
• Decimali finiti: Hanno un numero finito di cifre dopo la virgola. Esempio: 2,5 (si può scrivere anche come 2,5000... ma si ferma al 5).
• Decimali infiniti periodici: Hanno un numero infinito di cifre dopo la virgola, ma un gruppo di cifre (il periodo) si ripete all'infinito. Esempio: 1,3333... oppure 0,123123123...
• Decimali infiniti non periodici: Hanno un numero infinito di cifre dopo la virgola, ma non c'è un gruppo di cifre che si ripete. Questi numeri sono irrazionali. Esempio: π (pi greco) ≈ 3,14159265...

Noi ci concentreremo sui decimali infiniti periodici, perché è lì che entrano in gioco il periodo e l'antiperiodo.

Il Periodo: Il Ritmo Ripetitivo del Decimale

Il periodo è la sequenza di cifre che si ripete all'infinito dopo la virgola in un numero decimale periodico. È come il ritornello di una canzone, che continua a ripetersi. Per identificare il periodo, basta osservare la sequenza di cifre che si ripete. Ad esempio:

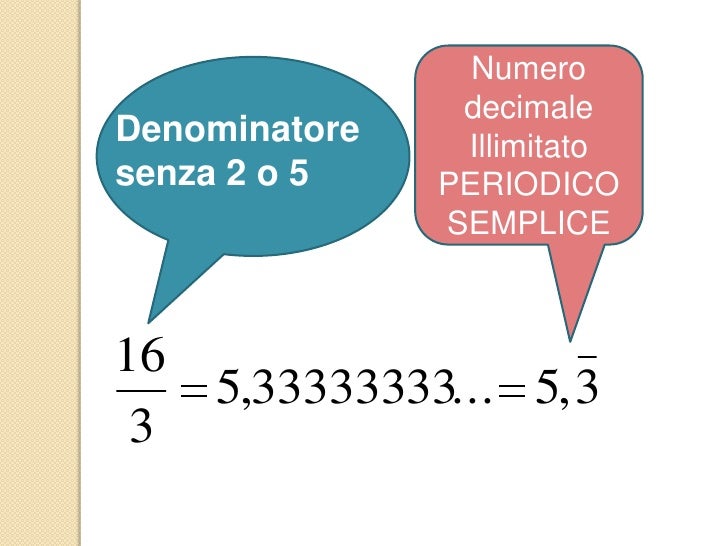
• Nel numero 3,3333..., il periodo è "3".
• Nel numero 1,272727..., il periodo è "27".
• Nel numero 0,123451234512345..., il periodo è "12345".

Per indicare che un numero è periodico, spesso si usa una barra sopra il periodo. Ad esempio, 3,3 per indicare 3,3333... oppure 1,27 per indicare 1,272727....

L'Antiperiodo: La Parte Che Viene Prima del Ritmo

L'antiperiodo è la sequenza di cifre che si trova tra la virgola e l'inizio del periodo. Non tutti i numeri decimali periodici hanno un antiperiodo. Se non c'è un antiperiodo, si dice che il numero è un periodico semplice. Se c'è, si dice che il numero è un periodico misto. Pensa all'antiperiodo come all'introduzione di una canzone, che precede il ritornello.

Ecco alcuni esempi per chiarire il concetto:

• Nel numero 0,3, non c'è antiperiodo. È un decimale periodico semplice.
• Nel numero 1,27, non c'è antiperiodo. È un decimale periodico semplice.
• Nel numero 0,53, l'antiperiodo è "5" e il periodo è "3". È un decimale periodico misto.
• Nel numero 2,1234, l'antiperiodo è "12" e il periodo è "34". È un decimale periodico misto.

Come puoi vedere, l'antiperiodo è cruciale per distinguere i numeri periodici semplici dai numeri periodici misti.

Come Trovare Periodo e Antiperiodo? Esempi Pratici

Ora che conosciamo le definizioni, vediamo come trovare il periodo e l'antiperiodo in pratica. Segui questi semplici passaggi:

1. Osserva il numero decimale: Individua la parte frazionaria (le cifre dopo la virgola).
2. Cerca una sequenza ripetuta: Cerca un gruppo di cifre che si ripete all'infinito. Questa è il periodo.
3. Identifica l'antiperiodo (se presente): Se ci sono cifre tra la virgola e l'inizio del periodo, quelle sono l'antiperiodo.

Vediamo alcuni esempi:

Esempio 1: 5,232323...

La parte frazionaria è "232323...". La sequenza "23" si ripete all'infinito. Quindi, il periodo è "23". Non ci sono cifre tra la virgola e l'inizio del periodo. Quindi, non c'è antiperiodo. Questo è un decimale periodico semplice.

Esempio 2: 0,166666...

La parte frazionaria è "166666...". La sequenza "6" si ripete all'infinito. Quindi, il periodo è "6". C'è una cifra ("1") tra la virgola e l'inizio del periodo. Quindi, l'antiperiodo è "1". Questo è un decimale periodico misto.

Esempio 3: 1,457777...

La parte frazionaria è "457777...". La sequenza "7" si ripete all'infinito. Quindi, il periodo è "7". Ci sono due cifre ("45") tra la virgola e l'inizio del periodo. Quindi, l'antiperiodo è "45". Questo è un decimale periodico misto.

Perché Periodo e Antiperiodo sono Importanti? La Relazione con le Frazioni

La comprensione del periodo e dell'antiperiodo non è solo un esercizio teorico. Ha un'importanza pratica perché ogni numero decimale periodico può essere espresso come una frazione. Questa è una delle proprietà fondamentali dei numeri razionali (i numeri che possono essere espressi come una frazione di due numeri interi).

Esiste una formula per convertire un numero decimale periodico in una frazione, che coinvolge il periodo e l'antiperiodo. Anche se non entreremo nei dettagli della formula in questo articolo (potrebbe essere un argomento per un articolo futuro!), è importante sapere che questa conversione è possibile.

Ad esempio, il numero 0,3333... può essere espresso come la frazione 1/3. Il numero 0,16666... può essere espresso come la frazione 1/6.

Questa relazione tra numeri decimali periodici e frazioni è fondamentale per comprendere la struttura dei numeri razionali e le operazioni che si possono eseguire con essi.

Errori Comuni e Come Evitarli

Quando si lavora con periodo e antiperiodo, è facile commettere alcuni errori comuni. Ecco alcuni suggerimenti per evitarli:

• Confondere periodo e antiperiodo: Ricorda, il periodo è la sequenza che si ripete, mentre l'antiperiodo è la sequenza che precede il periodo.
• Non riconoscere il periodo: A volte, il periodo può essere più lungo e più difficile da individuare. Osserva attentamente la sequenza di cifre.
• Ignorare l'antiperiodo: Non dimenticare di controllare se c'è un antiperiodo. Se lo ignori, potresti classificare erroneamente un numero come periodico semplice invece che misto.
• Confondere numeri periodici con non periodici: Un numero decimale periodico ha un *pattern* ripetitivo. Un numero decimale *non* periodico continua all'infinito *senza* un pattern ripetitivo.

La pratica rende perfetti! Più esercizi farai, più facile sarà individuare il periodo e l'antiperiodo.

Conclusione: Un Nuovo Modo di Vedere i Numeri Decimali

Spero che questo articolo ti abbia aiutato a comprendere meglio il periodo e l'antiperiodo dei numeri decimali. Ora hai gli strumenti per identificare questi elementi e per apprezzare la profonda connessione tra numeri decimali periodici e frazioni.

Ricorda, la matematica non è solo un insieme di formule astratte, ma un modo per comprendere il mondo che ci circonda. Ogni volta che ti imbatterai in un numero decimale periodico, pensa al ritmo del periodo e all'introduzione dell'antiperiodo. Questa nuova prospettiva ti renderà un matematico più consapevole e confidente.

Continua a esplorare, a sperimentare e a porre domande. Il mondo dei numeri è vasto e affascinante, e c'è sempre qualcosa di nuovo da imparare!