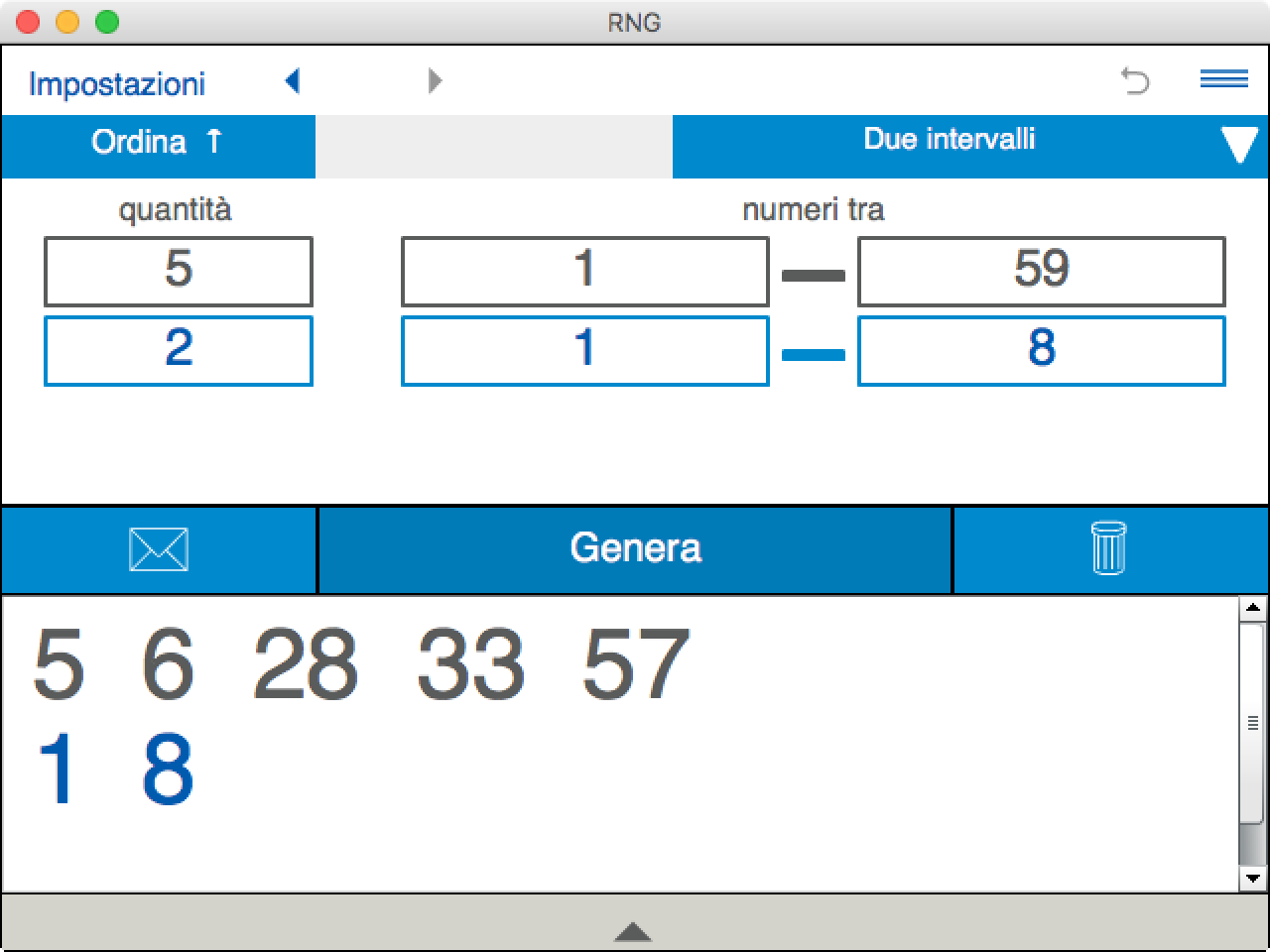
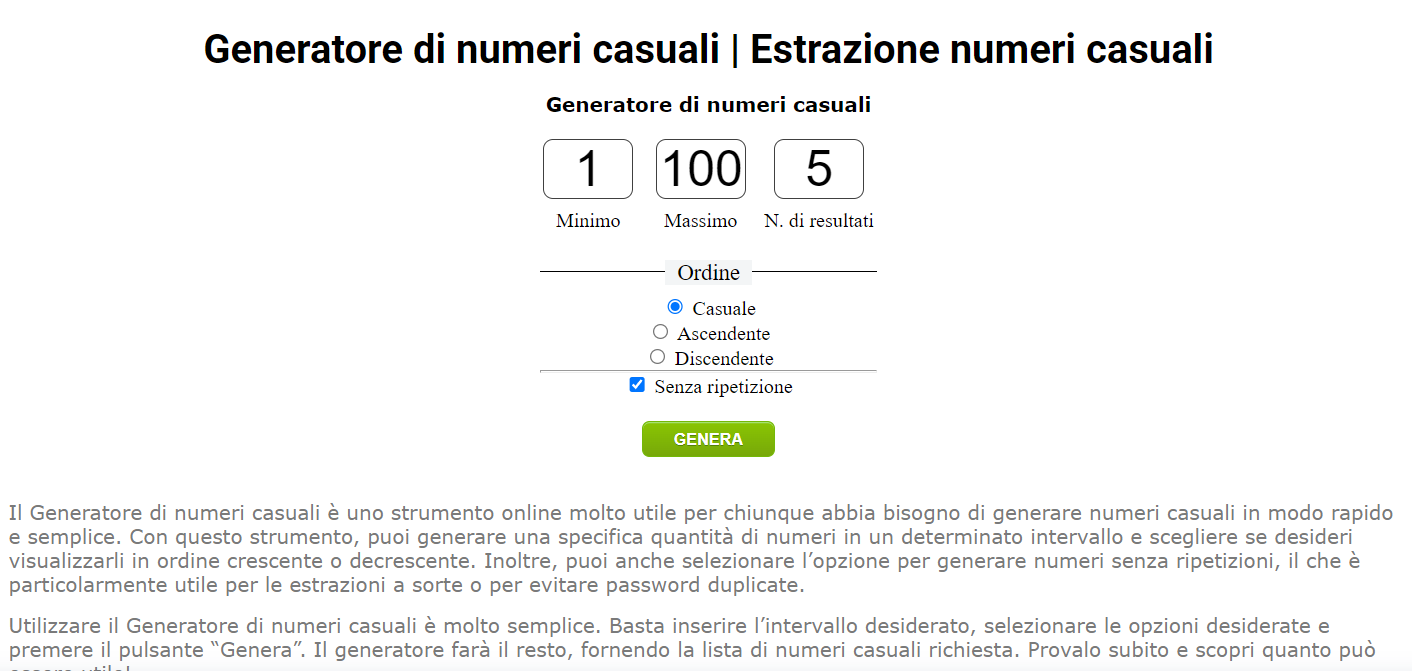
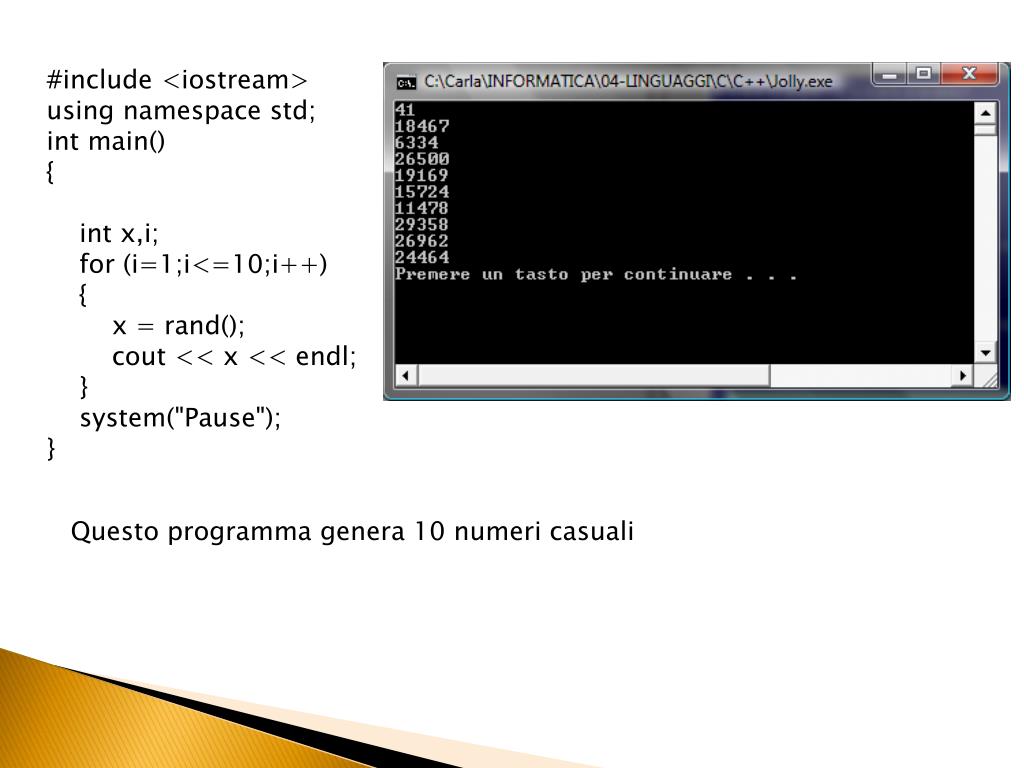
Numero Casuale Da 1 A 2

L'esigenza di generare un numero casuale compreso tra 1 e 1 è sorprendentemente comune in diversi ambiti, dalla programmazione al gaming, dalle simulazioni statistiche alla crittografia. Sebbene possa sembrare un compito banale, la generazione di numeri casuali, anche in un intervallo ristretto come questo, richiede una comprensione dei principi sottostanti e delle diverse tecniche disponibili.

La Definizione di "Casuale"

Prima di tutto, è fondamentale definire cosa intendiamo per "casuale". In termini rigorosi, un numero casuale ideale dovrebbe soddisfare alcune proprietà chiave: uniformità (ogni numero nell'intervallo ha la stessa probabilità di essere generato), indipendenza (ogni numero generato è indipendente dai precedenti) e imprevedibilità (non si può predire il numero successivo). Tuttavia, i generatori di numeri casuali (RNG) che utilizziamo nella pratica sono spesso pseudo-casuali. Ciò significa che generano sequenze di numeri che *sembrano* casuali ma sono in realtà determinate da un algoritmo e da un valore iniziale (seed).

Pseudo-casualità vs. Vera Casualità

I generatori di numeri pseudo-casuali (PRNG) sono molto più efficienti dal punto di vista computazionale rispetto ai generatori di numeri casuali veri (TRNG). I TRNG si basano su fenomeni fisici, come il decadimento radioattivo o il rumore atmosferico, per produrre numeri veramente imprevedibili. Mentre i PRNG sono deterministici, se si conosce l'algoritmo e il seed, è possibile riprodurre la stessa sequenza di numeri. Per questo motivo, i TRNG sono preferiti per applicazioni di sicurezza critiche come la crittografia. Tuttavia, per molte applicazioni non critiche, i PRNG sono sufficientemente buoni.

Metodi per Generare un Numero Casuale Tra 1 e 1

A questo punto, concentriamoci sull'intervallo specifico richiesto: da 1 a 1. Si noti che l'intervallo contiene *solo* il numero 1. Questo semplifica enormemente il compito! A differenza della generazione di numeri casuali in intervalli più ampi, qui il risultato è predeterminato. Tuttavia, è utile esplorare come diversi linguaggi di programmazione o sistemi gestirebbero questa richiesta, per comprendere meglio i concetti sottostanti.

Implementazioni in Diversi Linguaggi di Programmazione

Anche se il risultato è sempre 1, analizziamo come si potrebbe teoricamente implementare una funzione di generazione di numeri casuali tra 1 e 1 in diversi linguaggi:

* Python: ```python import random def numero_casuale_tra_1_e_1(): """Restituisce sempre 1.""" return 1 # oppure, per simulare un processo di "generazione": def numero_casuale_tra_1_e_1_simulato(): return int(random.random() + 1) #Questo restituirà sempre 1, ma usa un PRNG. ``` Anche usando `random.random()`, il risultato finale, dopo aver aggiunto 1 e troncato con `int()`, sarà sempre 1. * Java: ```java import java.util.Random; public class RandomNumber { public static int numeroCasualeTra1e1() { return 1; } //Simulazione public static int numeroCasualeTra1e1Simulato(){ Random random = new Random(); return 1; //anche usando il random, restituiremo sempre 1 } } ``` * JavaScript: ```javascript function numeroCasualeTra1e1() { return 1; } //Simulazione: function numeroCasualeTra1e1Simulato(){ return Math.floor(Math.random() + 1); //Restituisce sempre 1. } ```

Come si può notare, in tutti questi esempi, la funzione più semplice è quella che restituisce direttamente 1. Anche usando le funzioni `random()` fornite dai linguaggi, il risultato, dopo le necessarie trasformazioni (se applicate), sarà sempre 1. L'utilizzo di `random()` in questo contesto è computazionalmente inefficiente ma serve a illustrare il concetto.

Ottimizzazione e Considerazioni sulle Performance

In questo caso specifico, l'ottimizzazione è banale. La soluzione più efficiente è quella di evitare qualsiasi calcolo e restituire semplicemente il valore 1. Non ci sono algoritmi più veloci o più precisi per generare un numero casuale tra 1 e 1, perché il risultato è intrinsecamente determinato.

Casi d'Uso (anche se limitati)

Anche se la generazione di un numero casuale tra 1 e 1 sembra inutile, si possono immaginare scenari in cui una funzione che fa questo rientra in un contesto più ampio:

* Test Unitari: Potrebbe essere parte di un test unitario per verificare che una funzione gestisca correttamente un intervallo limitato. Anche se la funzione testata dovrebbe restituire sempre 1, il test verifica che non ci siano errori o eccezioni quando l'intervallo è ristretto. * Astrazione: In un sistema complesso, potrebbe esistere un'interfaccia per generare numeri casuali in intervalli diversi. La funzione che genera "un numero casuale tra 1 e 1" sarebbe un'implementazione specifica di questa interfaccia. * Debug: Durante il debug di un algoritmo che genera numeri casuali in intervalli più ampi, si potrebbe voler forzare un intervallo molto piccolo (come 1-1) per semplificare il debugging e isolare potenziali problemi. * Esempio Didattico: Proprio come questo articolo, può essere un esempio didattico per spiegare i concetti di base della generazione di numeri casuali e i limiti dei generatori pseudo-casuali.

Un Esempio Reale (Stilizzato)

Immaginiamo un gioco in cui un personaggio deve raccogliere un oggetto. La probabilità di trovare l'oggetto è determinata da un generatore di numeri casuali. Se la probabilità di trovare l'oggetto è impostata al 100%, l'algoritmo potrebbe utilizzare una funzione che restituisce sempre 1, simulando così la certezza di trovare l'oggetto.

Sicurezza e Implicazioni

In questo caso specifico, non ci sono implicazioni di sicurezza significative. La funzione restituisce sempre 1, quindi non c'è rischio di prevedibilità o vulnerabilità sfruttabili. Tuttavia, è importante ricordare che la sicurezza della generazione di numeri casuali diventa cruciale in applicazioni come la crittografia, la generazione di chiavi, e i giochi d'azzardo online. In questi contesti, è fondamentale utilizzare generatori di numeri casuali veri o generatori pseudo-casuali robusti e ben testati.

L'utilizzo di PRNG deboli in contesti di sicurezza può portare a gravi conseguenze. Ad esempio, se un attaccante è in grado di predire la sequenza di numeri generata da un PRNG, può rompere la crittografia, falsificare transazioni o manipolare il gioco.

Conclusioni

Sebbene generare un "numero casuale" tra 1 e 1 possa sembrare un esercizio triviale, ci permette di riflettere sui concetti fondamentali della generazione di numeri casuali, sulla differenza tra vera casualità e pseudo-casualità, e sull'importanza di scegliere l'algoritmo appropriato per l'applicazione desiderata. Ricorda: La soluzione più semplice ed efficiente in questo caso è sempre quella corretta: restituire direttamente 1. Anche simulare la "casualità" con un PRNG è computazionalmente inefficiente, ma può servire a fini didattici o di testing.

Se hai trovato questo articolo utile, sperimenta con diversi intervalli e linguaggi di programmazione per approfondire la tua comprensione della generazione di numeri casuali! Esplora librerie di generazione di numeri casuali più complesse e prova a implementare i tuoi algoritmi. La pratica è il modo migliore per imparare!