Numeri Primi Da 1 A 1000

Benvenuti in questo viaggio alla scoperta dei numeri primi compresi tra 1 e 1000. Un argomento affascinante che, pur essendo radicato nella matematica pura, trova applicazioni sorprendenti nella vita di tutti i giorni, in particolare nel campo della crittografia e della sicurezza informatica. In questo articolo, esploreremo cosa sono i numeri primi, come identificarli, e vedremo alcuni esempi concreti della loro importanza.

Cosa Sono i Numeri Primi?

Un numero primo è un numero naturale maggiore di 1 che ammette solamente due divisori: 1 e se stesso. In altre parole, non può essere diviso esattamente per nessun altro numero intero positivo al di fuori di 1 e del numero stesso. Il numero 1, per convenzione, non è considerato un numero primo.

Alcuni esempi semplici di numeri primi sono: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, e così via.

Per contro, un numero che ha più di due divisori è chiamato numero composto. Ad esempio, 4 è un numero composto perché è divisibile per 1, 2 e 4.

Perché il Numero 1 Non è Primo?

La definizione di numero primo, come abbiamo visto, richiede esattamente due divisori distinti. Il numero 1 ha solo un divisore (se stesso). Se includessimo 1 come numero primo, molte teoremi fondamentali dell'aritmetica, come il teorema fondamentale dell'aritmetica, diventerebbero più complessi da formulare e dimostrare. Quest'ultimo afferma che ogni numero intero maggiore di 1 può essere espresso in modo univoco come prodotto di numeri primi (a meno dell'ordine dei fattori).

Come Trovare i Numeri Primi tra 1 e 1000

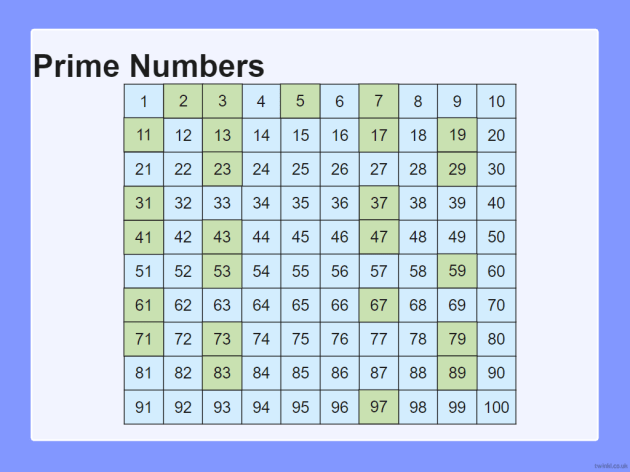
Trovare i numeri primi entro un determinato intervallo richiede un metodo sistematico. Il metodo più antico e famoso è il Crivello di Eratostene.

Il Crivello di Eratostene

Il Crivello di Eratostene è un algoritmo semplice ed efficiente per trovare tutti i numeri primi fino a un dato limite. Ecco come funziona:

1. Si crea una lista di tutti i numeri interi da 2 fino al limite desiderato (nel nostro caso, 1000).
2. Si inizia con il primo numero della lista, che è 2. 2 è un numero primo.
3. Si cancellano dalla lista tutti i multipli di 2 (4, 6, 8, 10, ecc.).
4. Si passa al numero successivo non cancellato nella lista, che è 3. 3 è un numero primo.
5. Si cancellano dalla lista tutti i multipli di 3 (9, 12, 15, 18, ecc.).
6. Si continua questo processo, trovando il numero successivo non cancellato (che sarà sempre un numero primo) e cancellando tutti i suoi multipli.
7. Si ferma quando il quadrato del numero corrente è maggiore del limite desiderato (nel nostro caso, 1000).
8. Tutti i numeri rimasti nella lista sono numeri primi.

Questo metodo è relativamente semplice da implementare sia manualmente che con un programma per computer.

Lista dei Numeri Primi tra 1 e 1000 (Parziale)

Ecco un elenco parziale dei numeri primi tra 1 e 1000 per darvi un'idea. L'elenco completo è abbastanza lungo!

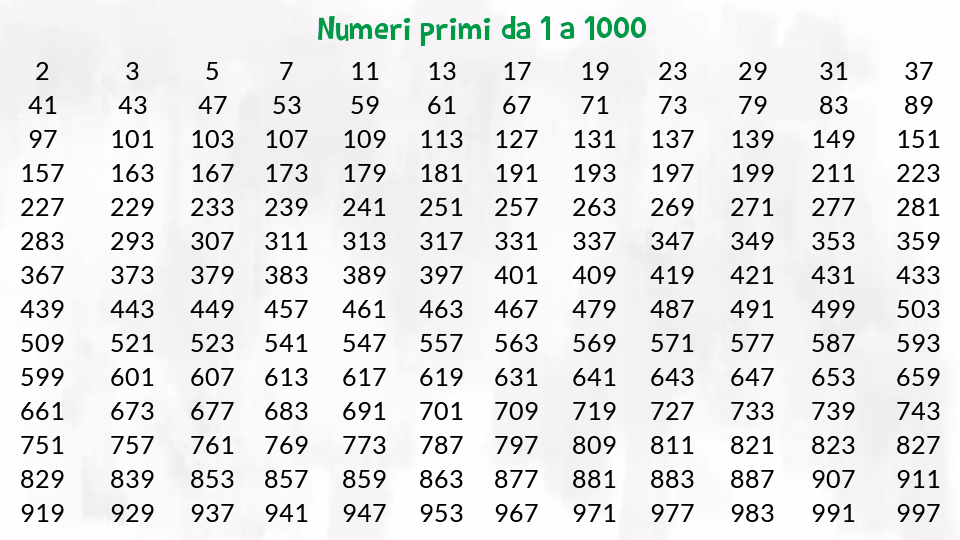
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997.

Ci sono 168 numeri primi tra 1 e 1000.

Applicazioni Pratiche dei Numeri Primi

I numeri primi non sono solo un'astrazione matematica. Hanno applicazioni cruciali nel mondo reale, in particolare nel campo della crittografia.

Crittografia a Chiave Pubblica (RSA)

Uno degli algoritmi di crittografia più utilizzati al mondo, l'RSA (Rivest-Shamir-Adleman), si basa pesantemente sulla difficoltà di fattorizzare numeri molto grandi in numeri primi. In sostanza, l'algoritmo funziona così:

1. Si scelgono due numeri primi grandi, p e q.
2. Si calcola il loro prodotto, n = p * q. n è la chiave pubblica.
3. Si calcola la funzione di Eulero, φ(n) = (p-1) * (q-1).
4. Si sceglie un numero e tale che 1 < e < φ(n) e che e sia coprimo con φ(n) (cioè, il loro massimo comun divisore è 1). e fa parte della chiave pubblica.
5. Si calcola l'inverso moltiplicativo di e modulo φ(n), chiamato d. d è la chiave privata.

Per crittografare un messaggio, si utilizza la chiave pubblica (n ed e). Per decrittografare il messaggio, si utilizza la chiave privata (d). La sicurezza dell'RSA si basa sul fatto che è estremamente difficile fattorizzare n in p e q se p e q sono numeri primi sufficientemente grandi (centinaia o migliaia di cifre). Un attacco per "rompere" la crittografia RSA richiederebbe una potenza di calcolo enorme e molto tempo.

Altri Usi della Crittografia

La crittografia basata su numeri primi è utilizzata per proteggere le nostre comunicazioni online, le transazioni bancarie, e-commerce, firme digitali, e molto altro. Ogni volta che vedete il simbolo del lucchetto nel vostro browser, è probabile che la crittografia basata su numeri primi stia proteggendo la vostra connessione.

Conclusione

I numeri primi, pur essendo concetti matematici apparentemente astratti, hanno un impatto significativo sulla nostra vita quotidiana. La loro importanza nella crittografia e nella sicurezza informatica è innegabile. Senza di essi, il mondo digitale come lo conosciamo non sarebbe possibile.

Se siete interessati ad approfondire l'argomento, vi invito a esplorare ulteriormente il mondo dei numeri primi, le loro proprietà, e le loro applicazioni in vari campi della scienza e della tecnologia. Potreste scoprire che la matematica, apparentemente distante dalla vita di tutti i giorni, è in realtà fondamentale per il funzionamento del mondo moderno.