Numeri Primi Da 1 A 100

Capita a tutti, prima o poi, di imbattersi nei numeri primi. Magari a scuola, studiando matematica, o forse in qualche puzzle logico. Ma cosa sono esattamente? E perché sono così importanti? Se ti sei mai posto queste domande, sei nel posto giusto. Cercheremo di demistificare questo concetto, rendendolo accessibile e interessante, anche se la matematica non è il tuo forte. Sentiamo spesso dire che qualcosa è "fondamentale", e nel caso dei numeri primi, la parola è azzeccata. Sono i *mattoni* con cui si costruiscono tutti gli altri numeri. E l'elenco dei numeri primi da 1 a 100 è un ottimo punto di partenza per capirne il funzionamento.

Cosa sono i numeri primi?

Un numero primo è un numero intero maggiore di 1 che ha solo due divisori: 1 e se stesso. In altre parole, non può essere diviso esattamente per nessun altro numero a parte 1 e lui stesso. Ad esempio, 7 è un numero primo perché può essere diviso solo per 1 e per 7. Il numero 4, invece, non è primo perché può essere diviso per 1, 2 e 4. Quindi, 4 è un numero composto.

Può sembrare un concetto semplice, ma i numeri primi hanno implicazioni profonde in diversi campi, dalla crittografia alla fisica. Pensaci: la sicurezza delle nostre transazioni online, in gran parte, dipende dalla difficoltà di fattorizzare numeri molto grandi in numeri primi!

Perché 1 non è considerato un numero primo?

Questa è una domanda che sorge spontanea. Il motivo è legato al Teorema Fondamentale dell'Aritmetica. Questo teorema afferma che ogni numero intero maggiore di 1 può essere espresso in modo univoco come prodotto di numeri primi (a meno dell'ordine dei fattori). Se includessimo 1 come numero primo, questa unicità verrebbe meno. Ad esempio, 12 potrebbe essere scritto come 2 x 2 x 3, ma anche come 1 x 2 x 2 x 3, 1 x 1 x 2 x 2 x 3, e così via. Escludendo 1, manteniamo l'eleganza e l'utilità del teorema.

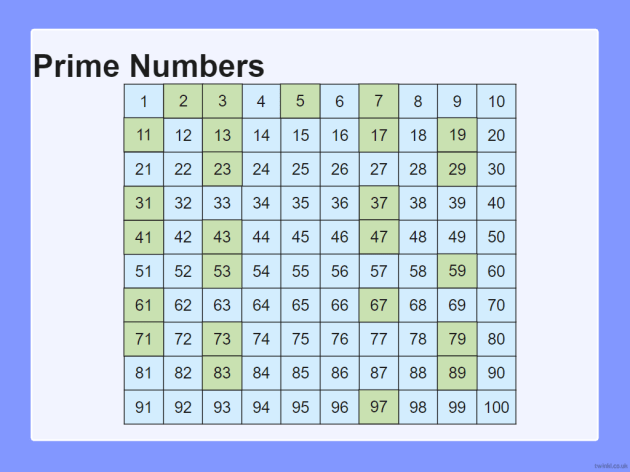
I numeri primi da 1 a 100: un elenco

Ecco l'elenco dei numeri primi compresi tra 1 e 100:

• 2
• 3
• 5
• 7
• 11
• 13
• 17
• 19
• 23
• 29
• 31
• 37
• 41
• 43
• 47
• 53
• 59
• 61
• 67
• 71
• 73
• 79
• 83
• 89
• 97

Sono 25 in totale. Nota come diventano meno frequenti man mano che si sale con i numeri. Questo è un fenomeno noto e studiato dai matematici. Non esiste una formula semplice per generare tutti i numeri primi, il che li rende ancora più affascinanti.

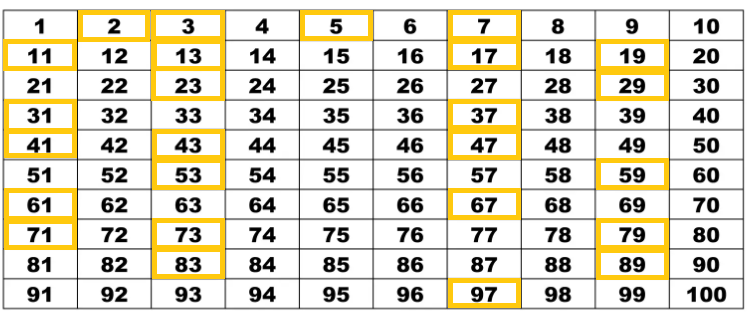
Come trovare i numeri primi: il crivello di Eratostene

Esiste un metodo antico, ma ancora valido, per identificare i numeri primi: il crivello di Eratostene. Immagina di scrivere tutti i numeri da 2 a 100 in una tabella. Poi:

• Inizia con il primo numero primo, 2. Cerchia 2.
• Cancella tutti i multipli di 2 (4, 6, 8, ecc.).
• Passa al numero successivo non cancellato, che è 3. Cerchia 3.
• Cancella tutti i multipli di 3 (6, 9, 12, ecc.). Nota che alcuni di questi, come 6, sono già stati cancellati.
• Continua così, passando al numero successivo non cancellato, cerchiandolo e cancellando tutti i suoi multipli.
• Quando hai finito, tutti i numeri cerchiati sono i numeri primi.

Il crivello di Eratostene è un algoritmo semplice ed efficace per trovare i numeri primi entro un certo intervallo. È un ottimo esempio di come un'idea brillante possa risolvere un problema complesso in modo elegante.

Applicazioni reali dei numeri primi

Come accennato in precedenza, i numeri primi sono fondamentali per la crittografia. Molti algoritmi di crittografia, come l'RSA, si basano sulla difficoltà di fattorizzare numeri molto grandi in numeri primi. Più grandi sono i numeri primi utilizzati, più sicura è la crittografia. Quando fai acquisti online o accedi al tuo conto bancario, stai usando, senza saperlo, la matematica dei numeri primi per proteggere le tue informazioni.

Ma non solo crittografia! I numeri primi trovano applicazioni anche in:

• Informatica: nella generazione di numeri casuali e nella creazione di tabelle hash efficienti.
• Fisica: in alcune teorie sulla distribuzione dei numeri primi e la loro relazione con i sistemi caotici.
• Musica: Alcuni compositori hanno esplorato l'uso di sequenze di numeri primi nella composizione musicale.

Controversie e Curiosità

Esiste una controversia aperta sui numeri primi gemelli (coppie di numeri primi che differiscono di 2, come 3 e 5, 5 e 7, 11 e 13). L'ipotesi dei numeri primi gemelli afferma che ci sono infiniti numeri primi gemelli, ma nessuno è ancora riuscito a dimostrarlo definitivamente. Questa è solo una delle tante domande irrisolte sui numeri primi che continuano a sfidare i matematici di tutto il mondo.

Un'altra curiosità è che la distribuzione dei numeri primi sembra essere abbastanza casuale, ma allo stesso tempo segue schemi statistici ben definiti. Questa dualità affascina i matematici da secoli e ha portato a importanti scoperte nella teoria dei numeri.

Oltre i primi 100: la ricerca continua

Abbiamo visto i numeri primi da 1 a 100, ma i numeri primi sono infiniti. Trovare numeri primi sempre più grandi è una sfida continua per i matematici e gli informatici. Esistono progetti di calcolo distribuito, come il Great Internet Mersenne Prime Search (GIMPS), in cui volontari di tutto il mondo contribuiscono con la potenza di calcolo dei loro computer per cercare nuovi numeri primi di Mersenne (numeri primi della forma 2ⁿ - 1). Questi numeri primi, per via della loro forma specifica, sono più facili da testare e spesso detengono il record di numero primo più grande conosciuto.

L'importanza di questa ricerca non è solo teorica. Numeri primi sempre più grandi significano crittografie più sicure e progressi nella comprensione della struttura dei numeri. La ricerca dei numeri primi è una finestra aperta sull'infinito e sulla bellezza nascosta della matematica.

Numeri Primi: Difficoltà di calcolo e sicurezza informatica

La vera potenza dei numeri primi, in termini di sicurezza informatica, risiede nella difficoltà intrinseca di fattorizzare numeri molto grandi. Fattorizzare un numero significa trovare i numeri primi che, moltiplicati tra loro, danno quel numero. Ad esempio, fattorizzare 15 è semplice: 3 x 5. Ma fattorizzare un numero di centinaia di cifre richiede una quantità di calcolo che è proibitiva anche per i computer più potenti.

Questo concetto è alla base di algoritmi come RSA. Quando si genera una chiave RSA, si scelgono due numeri primi molto grandi, p e q, e si calcola il loro prodotto n = p x q. Il numero n viene reso pubblico (è la chiave pubblica), mentre i numeri primi p e q vengono mantenuti segreti (sono la chiave privata). Chiunque può usare la chiave pubblica per criptare un messaggio, ma solo chi conosce la chiave privata (p e q) può decriptarlo. Questo perché, per decriptare il messaggio, è necessario fattorizzare n, e come abbiamo detto, questa operazione è estremamente difficile.

L'emergere dei computer quantistici rappresenta una potenziale minaccia per la crittografia basata sui numeri primi. Gli algoritmi quantistici, come l'algoritmo di Shor, sono in grado di fattorizzare numeri molto grandi in tempi significativamente inferiori rispetto agli algoritmi classici. Tuttavia, la tecnologia dei computer quantistici è ancora in fase di sviluppo, e ci sono sforzi significativi in corso per sviluppare algoritmi di crittografia resistenti agli attacchi quantistici (crittografia post-quantistica). Questa è una corsa agli armamenti continua tra i crittografi e i potenziali attaccanti.

In sintesi: cosa ci portiamo a casa

I numeri primi, pur essendo un concetto matematico apparentemente semplice, sono alla base di molte tecnologie che utilizziamo quotidianamente. Dalla sicurezza delle nostre transazioni online alla ricerca di nuovi algoritmi di crittografia, i numeri primi continuano a giocare un ruolo cruciale nel mondo moderno. La loro natura misteriosa e la loro distribuzione apparentemente casuale continuano a sfidare i matematici e ad affascinare chiunque si avvicini a questo argomento.

Ricordati:

• Un numero primo è divisibile solo per 1 e per se stesso.
• I numeri primi da 1 a 100 sono: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
• Il crivello di Eratostene è un metodo semplice per trovare i numeri primi.
• I numeri primi sono fondamentali per la crittografia.

Spero che questa introduzione ai numeri primi ti sia stata utile. Ora che hai una conoscenza di base, sei pronto per esplorare argomenti più avanzati, come la teoria dei numeri o la crittografia. Oppure, semplicemente, puoi provare a risolvere qualche puzzle logico che coinvolge i numeri primi. Le possibilità sono infinite!

Qual è la cosa più interessante che hai imparato sui numeri primi? Ti incuriosisce il loro ruolo nella crittografia, la loro distribuzione misteriosa o la difficoltà di trovarne di sempre più grandi?