Numeri Dispari Da 1 A 100

Quante volte ci siamo trovati di fronte a un problema apparentemente semplice, ma che nasconde una miriade di sfumature? Pensiamo, ad esempio, all'insieme dei numeri dispari da 1 a 100. A prima vista, un elenco. Ma scavando più a fondo, scopriamo pattern, applicazioni pratiche e persino una connessione inaspettata con la matematica e la vita di tutti i giorni. Capire i numeri dispari non è solo un esercizio matematico, è affinare la nostra capacità di osservazione e problem-solving.

Immagina di dover dividere un gruppo di 99 persone in coppie per un ballo di gruppo. Avrai sempre una persona che rimane fuori. Quel "rimanere fuori" è l'essenza di un numero dispari. Forse hai un progetto in cui devi assegnare delle risorse in modo equo, ma hai un budget che termina con un numero dispari. Come fai a gestire quella singola unità in più? Questi scenari quotidiani, che spesso trascuriamo, sono permeati dalla natura stessa dei numeri dispari.

Cosa sono i Numeri Dispari?

Fondamentalmente, un numero dispari è qualsiasi numero intero che non è divisibile per 2 senza lasciare un resto. In altre parole, se provi a dividerlo a metà, avrai sempre "qualcosa" in più. I numeri pari, al contrario, si dividono perfettamente a metà. Questa semplice definizione è la chiave per comprendere la loro peculiarità.

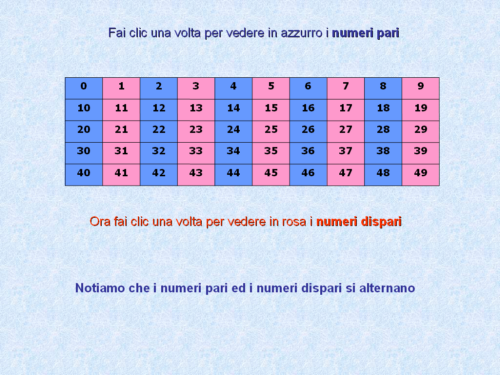
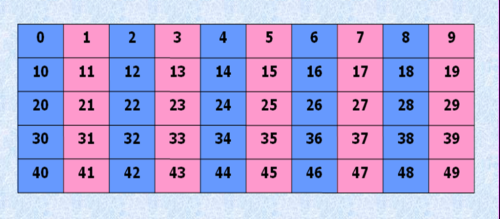
L'Elenco dei Numeri Dispari da 1 a 100

Ecco l'elenco completo dei numeri dispari da 1 a 100:

1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97, 99

Un'osservazione immediata è che ogni numero dispari è seguito da un numero pari, e viceversa. Questo crea un'alternanza costante, un ritmo prevedibile che li rende facili da identificare.

Applicazioni Pratiche dei Numeri Dispari

I numeri dispari non sono solo concetti astratti; hanno applicazioni concrete in diversi campi:

Informatica: Gli indirizzi di memoria possono spesso essere organizzati in modo che certi dati siano memorizzati solo in posizioni di memoria dispari.
Matematica: Molti teoremi e concetti matematici si basano sulla distinzione tra numeri pari e dispari, ad esempio nella teoria dei numeri.
Scienze: In fisica, le proprietà delle onde possono essere descritte usando numeri dispari, come nel caso degli armonici dispari.
Vita Quotidiana: Come accennato all'inizio, dividere oggetti o persone in gruppi equamente spesso si scontra con la realtà dei numeri dispari, richiedendo soluzioni creative. Pensate all'assegnazione dei posti a sedere ad un matrimonio con un numero dispari di invitati!

Controargomentazioni: Perché Alcuni Sottovalutano i Numeri Dispari

Alcuni potrebbero sostenere che la distinzione tra pari e dispari è banale, un semplice artificio matematico senza grande importanza. Potrebbero dire che concentrarsi su di essi è una perdita di tempo, dato che esistono concetti matematici molto più complessi e rilevanti. Tuttavia, questa visione è miope. La semplicità di un concetto non ne diminuisce il valore. Anzi, spesso sono i concetti più semplici a costituire le fondamenta per idee più complesse. Senza comprendere la differenza tra pari e dispari, sarebbe difficile affrontare problemi di divisibilità, congruenze e molti altri argomenti avanzati.

Inoltre, la loro onnipresenza nella vita quotidiana rende la loro comprensione fondamentale per un approccio pratico alla risoluzione dei problemi.

Pattern e Proprietà Interessanti

I numeri dispari nascondono pattern affascinanti. Ad esempio:

La somma dei primi n numeri dispari è uguale a n². (1 = 1², 1 + 3 = 4 = 2², 1 + 3 + 5 = 9 = 3², e così via). Questa è una proprietà notevole che collega direttamente i numeri dispari ai quadrati perfetti.
La differenza tra due numeri dispari consecutivi è sempre 2. Questa costanza rende la loro sequenza prevedibile e facile da generare.
Un numero dispari elevato a qualsiasi potenza positiva rimane sempre dispari. Questo contrasta con i numeri pari, che elevati a qualsiasi potenza positiva rimangono pari.

Questi pattern non sono solo curiosità matematiche; sono strumenti che possono essere utilizzati per semplificare calcoli e risolvere problemi in modo più efficiente.

Analogia: I Gradini di una Scala

Immagina una scala dove ogni gradino rappresenta un numero intero. I gradini pari sono lisci e regolari, permettendo di salire in modo uniforme. I gradini dispari, invece, hanno una piccola sporgenza, una sorta di "ostacolo" che impedisce un movimento completamente fluido. Questa sporgenza rappresenta il "resto" che rimane quando un numero dispari viene diviso per 2. Proprio come la sporgenza rende i gradini dispari un po' diversi, così il "resto" distingue i numeri dispari dai numeri pari.

Come Sfruttare la Conoscenza dei Numeri Dispari

Ora che abbiamo esplorato la natura e le applicazioni dei numeri dispari, vediamo come possiamo sfruttare questa conoscenza:

Problem-solving: Quando affronti un problema che coinvolge la divisibilità, considera se i numeri in questione sono pari o dispari. Questo può aiutarti a semplificare il problema e a trovare una soluzione più rapidamente.
Ottimizzazione: In informatica, comprendere come i dati vengono memorizzati in posizioni di memoria pari o dispari può aiutarti a ottimizzare il codice e a migliorare le prestazioni.
Creatività: Non aver paura di utilizzare i numeri dispari in modo creativo. Sperimenta con i pattern e le proprietà che abbiamo discusso per trovare nuove soluzioni a problemi complessi.

Ricorda: la matematica non è solo un insieme di regole e formule; è uno strumento potente per comprendere il mondo che ci circonda. E anche i concetti apparentemente più semplici, come i numeri dispari, possono rivelarsi sorprendentemente utili.

Un Esempio Pratico

Supponiamo di dover disporre 55 sedie in file, in modo che ogni fila abbia lo stesso numero di sedie. Potremmo provare a dividere 55 per diversi numeri, ma sapere che 55 è dispari ci restringe immediatamente le possibilità. Sappiamo che non può essere diviso per 2, 4, 6, ecc. Questo ci fa risparmiare tempo e fatica, guidandoci verso le soluzioni possibili (5 file da 11 sedie, o 11 file da 5 sedie).

Conclusioni: Un Invito all'Azione

Abbiamo visto che i numeri dispari, pur nella loro semplicità, sono onnipresenti e portatori di importanti proprietà matematiche. La loro comprensione può aiutarci a risolvere problemi, a ottimizzare processi e a vedere il mondo sotto una luce diversa. Ma la vera conoscenza si acquisisce solo attraverso la pratica.

Quindi, ti invito a riflettere su quanto appreso. Pensa a un problema che hai affrontato di recente. Poteva essere risolto in modo più efficiente considerando se i numeri coinvolti erano pari o dispari? Come puoi applicare questa conoscenza in futuro per semplificare la tua vita o il tuo lavoro? Esplora, sperimenta e non smettere mai di imparare!

Quale nuovo pattern sui numeri dispari ti incuriosisce di più e come potresti investigarlo ulteriormente?