Moto Rettilineo Uniformemente Accelerato Legge Oraria

Il Moto Rettilineo Uniformemente Accelerato (MRUA) è uno dei concetti fondamentali della fisica che descrive il movimento di un oggetto lungo una linea retta con un'accelerazione costante. Comprendere questo tipo di moto è cruciale per analizzare una vasta gamma di fenomeni fisici, dalla caduta di un oggetto soggetto alla gravità, al movimento di un'automobile che accelera.
Definizione e Caratteristiche del MRUA
Il MRUA si distingue per la presenza di un'accelerazione costante. Questo significa che la velocità dell'oggetto cambia in modo uniforme nel tempo. A differenza del moto rettilineo uniforme (MRU), dove la velocità rimane costante, nel MRUA la velocità aumenta (o diminuisce, se l'accelerazione è negativa) linearmente con il tempo.
Variabili Chiave
Per descrivere completamente il MRUA, è necessario considerare le seguenti variabili:
- Posizione (s): La posizione dell'oggetto lungo la linea retta, misurata rispetto a un punto di riferimento.
- Velocità (v): La rapidità con cui l'oggetto si muove e la sua direzione.
- Accelerazione (a): Il tasso di variazione della velocità nel tempo. È costante nel MRUA.
- Tempo (t): La variabile indipendente che indica l'istante in cui si osserva il moto.
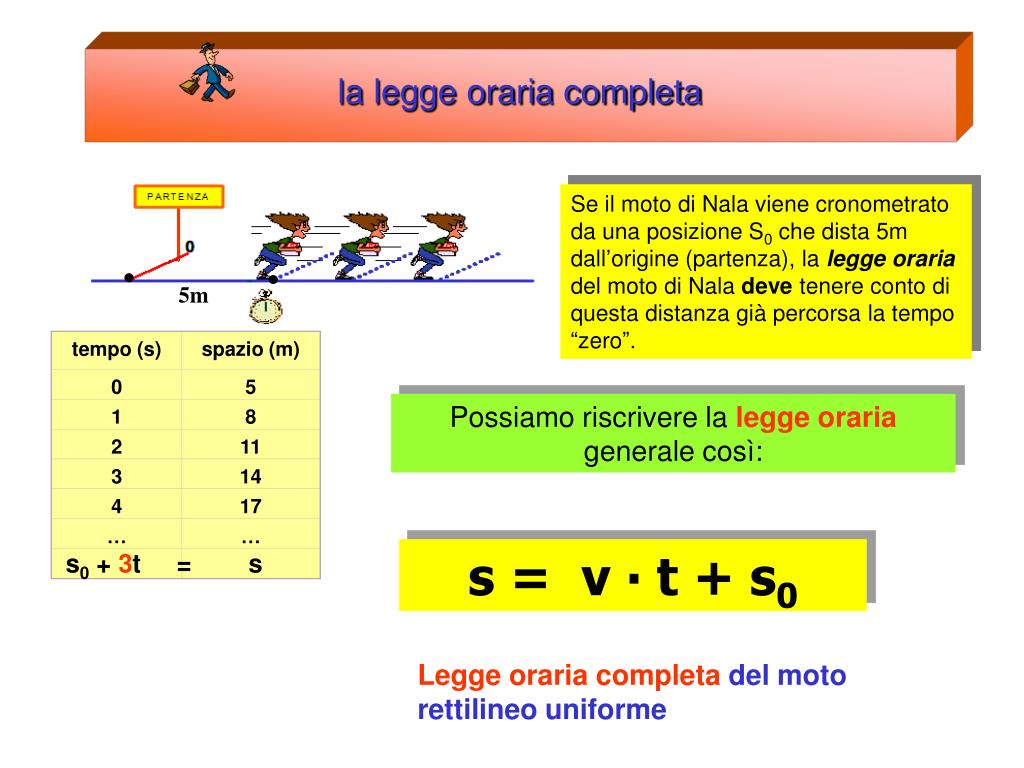
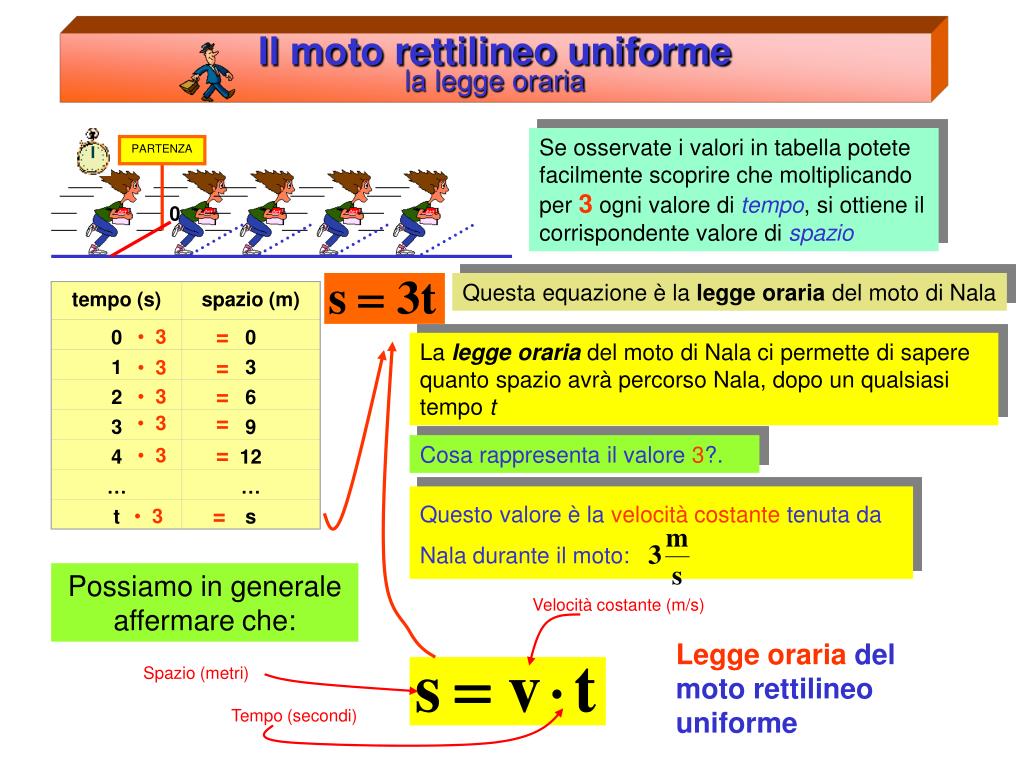
La Legge Oraria del MRUA
La legge oraria è un'equazione matematica che descrive la posizione di un oggetto in funzione del tempo. Per il MRUA, la legge oraria è data da:
s(t) = s0 + v0t + (1/2)at2
Dove:
- s(t) è la posizione dell'oggetto al tempo t.
- s0 è la posizione iniziale dell'oggetto al tempo t=0.
- v0 è la velocità iniziale dell'oggetto al tempo t=0.
- a è l'accelerazione costante.
- t è il tempo trascorso.
Questa equazione ci permette di determinare dove si trova l'oggetto in qualsiasi momento, conoscendo la sua posizione iniziale, la sua velocità iniziale e la sua accelerazione. È una formula fondamentale per risolvere problemi di cinematica.
Derivazione della Legge Oraria
La legge oraria può essere derivata utilizzando concetti di calcolo integrale. Sappiamo che l'accelerazione è la derivata della velocità rispetto al tempo (a = dv/dt) e che la velocità è la derivata della posizione rispetto al tempo (v = ds/dt). Integrando l'accelerazione costante rispetto al tempo, otteniamo la velocità in funzione del tempo:
v(t) = v0 + at
Successivamente, integrando la velocità in funzione del tempo rispetto al tempo, otteniamo la legge oraria:
s(t) = ∫ v(t) dt = ∫ (v0 + at) dt = s0 + v0t + (1/2)at2
La costante di integrazione s0 rappresenta la posizione iniziale dell'oggetto.
Altre Equazioni Utili nel MRUA
Oltre alla legge oraria, esistono altre equazioni utili per risolvere problemi di MRUA:
- Velocità in funzione del tempo: v(t) = v0 + at
- Equazione di Torricelli (velocità in funzione della posizione): v2 = v02 + 2a(s - s0)
L'equazione di Torricelli è particolarmente utile quando non si conosce il tempo, ma si conoscono la velocità iniziale, la velocità finale, l'accelerazione e la distanza percorsa.
Esempi Pratici e Dati Reali
Il MRUA si manifesta in una moltitudine di situazioni reali. Ecco alcuni esempi:
Caduta Libera di un Oggetto
Un esempio classico è la caduta libera di un oggetto. In assenza di resistenza dell'aria, un oggetto cade verso il suolo con un'accelerazione costante approssimativamente pari a 9.81 m/s2 (l'accelerazione di gravità, indicata con g). Possiamo applicare la legge oraria per calcolare la posizione dell'oggetto in funzione del tempo:
s(t) = s0 + v0t + (1/2)gt2
Se un oggetto viene lasciato cadere da un'altezza di 10 metri (s0 = 10 m) con una velocità iniziale di 0 m/s (v0 = 0 m/s), possiamo calcolare il tempo impiegato per raggiungere il suolo (s(t) = 0 m):
0 = 10 + 0*t + (1/2)(-9.81)t2
t = √(2 * 10 / 9.81) ≈ 1.43 s
Quindi, l'oggetto impiegherà circa 1.43 secondi per raggiungere il suolo.
Accelerazione di un'Automobile
Un altro esempio è l'accelerazione di un'automobile. Quando un'automobile accelera da ferma (v0 = 0 m/s) a una velocità di 100 km/h (circa 27.78 m/s) in 10 secondi, possiamo calcolare l'accelerazione media:
a = (v - v0) / t = (27.78 - 0) / 10 = 2.778 m/s2
Possiamo quindi utilizzare la legge oraria per calcolare la distanza percorsa dall'automobile durante questa accelerazione:
s(t) = s0 + v0t + (1/2)at2 = 0 + 0*10 + (1/2)(2.778)(10)2 = 138.9 m
L'automobile percorrerà circa 138.9 metri durante l'accelerazione.
Dati Reali: Test di Accelerazione delle Auto
Molte riviste automobilistiche effettuano test di accelerazione (0-100 km/h) per valutare le prestazioni delle auto. Questi test forniscono dati reali sull'accelerazione e sulla distanza percorsa durante il MRUA. Ad esempio, un'auto sportiva potrebbe accelerare da 0 a 100 km/h in 4 secondi. Conoscendo questi dati, possiamo calcolare l'accelerazione media e utilizzare la legge oraria per prevedere la distanza percorsa durante il test.
Limitazioni e Considerazioni
È importante notare che il modello del MRUA è un'idealizzazione. Nella realtà, l'accelerazione raramente è perfettamente costante. Fattori come la resistenza dell'aria, l'attrito e la variazione della potenza del motore possono influenzare l'accelerazione e rendere il moto più complesso. Tuttavia, il MRUA rimane un'approssimazione utile per analizzare molti fenomeni fisici e fornire una comprensione di base del movimento accelerato.
Un'altra limitazione è l'assenza di una forza esterna. Nel mondo reale, il moto di un corpo è determinato dall'applicazione di una forza. L'accelerazione è un effetto della forza, descritto dalla seconda legge di Newton.
Conclusione e Prossimi Passi
Il Moto Rettilineo Uniformemente Accelerato e la sua legge oraria sono strumenti essenziali per comprendere e analizzare il movimento accelerato. Attraverso la comprensione dei concetti di posizione, velocità, accelerazione e tempo, e applicando le equazioni appropriate, possiamo risolvere una vasta gamma di problemi di cinematica. Continuate ad esplorare concetti di fisica più avanzati, come il moto parabolico e la dinamica, per approfondire la vostra comprensione del mondo che ci circonda. Mettete in pratica le vostre conoscenze risolvendo esercizi e analizzando esempi reali!