Mappa Concettuale Sulla Retta Nel Piano Cartesiano

Capita a tutti, prima o poi, di sentirsi un po' persi di fronte alla matematica, soprattutto quando si tratta di concetti astratti come la geometria analitica. La retta nel piano cartesiano, per esempio, può sembrare un argomento ostico, pieno di formule e regole complicate. Ma non temere! Questo articolo è pensato proprio per te, per trasformare quella che percepisci come una sfida in un'opportunità di comprensione e, perché no, anche di divertimento.

Proviamo a immaginare la retta non come un'equazione fredda, ma come una linea guida, un percorso che ci aiuta a orientarci nel mondo che ci circonda. Pensa alle mappe stradali, ai grafici che mostrano l'andamento di un'azienda, o anche semplicemente alla traiettoria di una palla lanciata in aria. Dietro a queste immagini, spesso c'è una retta, un'equazione che ne descrive il movimento o la posizione.

Cos'è una Mappa Concettuale sulla Retta nel Piano Cartesiano?

Una mappa concettuale è uno strumento visuale che ti aiuta a organizzare e a comprendere le informazioni. Invece di memorizzare formule a memoria, la mappa concettuale ti permette di vedere come i diversi concetti sono collegati tra loro. Immagina di avere tutti i pezzi di un puzzle e di doverli assemblare per formare un'immagine chiara e completa. La mappa concettuale è il tuo schema di montaggio.

Nel caso specifico della retta nel piano cartesiano, la mappa concettuale ti aiuterà a collegare l'equazione della retta, la sua rappresentazione grafica, il concetto di pendenza (o coefficiente angolare) e l'intercetta (o termine noto). Avrai una visione d'insieme, che ti permetterà di affrontare gli esercizi con maggiore sicurezza e consapevolezza.

Costruire la Mappa Concettuale: I Concetti Chiave

Iniziamo ad analizzare i concetti fondamentali che compongono la nostra mappa:

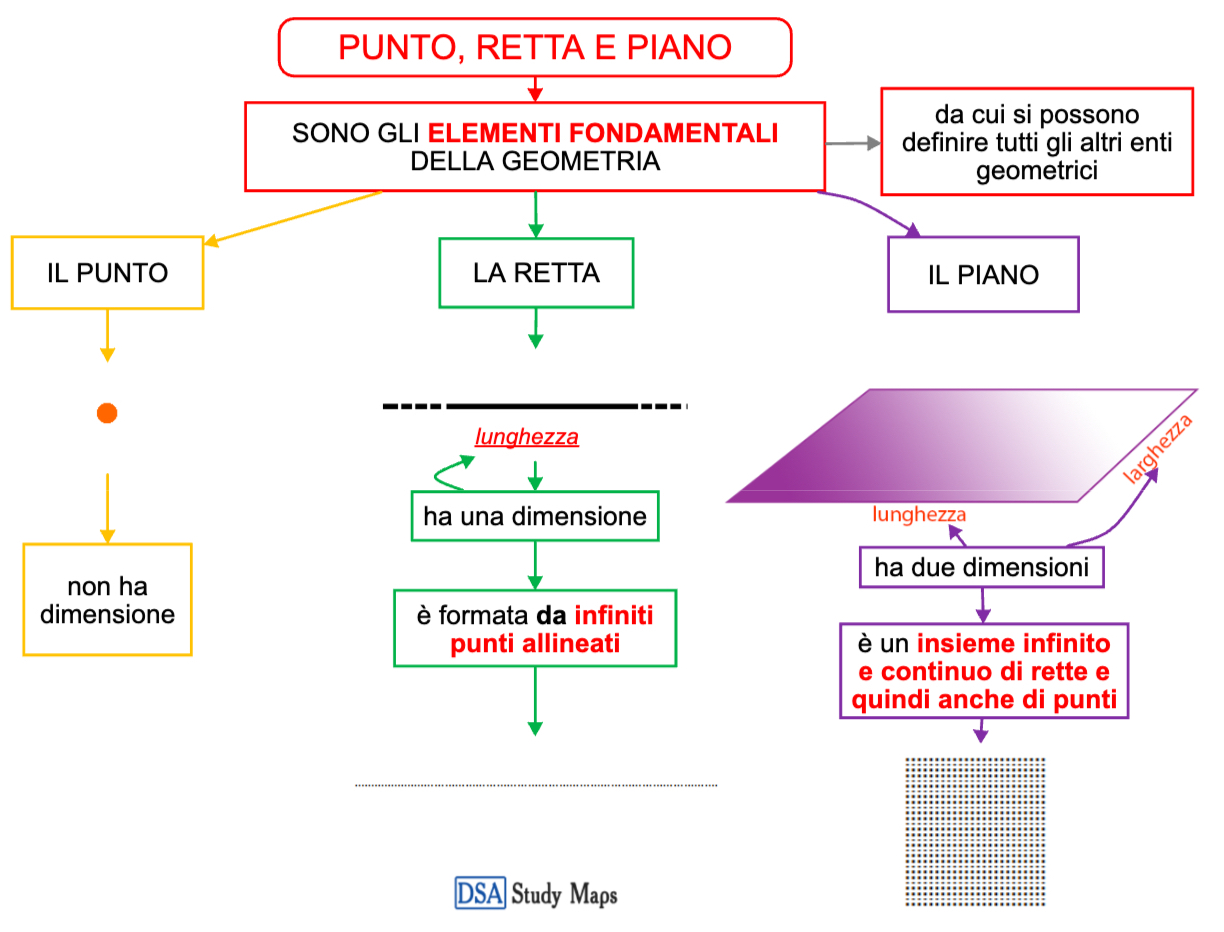
Piano Cartesiano: Il nostro punto di partenza è il piano cartesiano, un sistema di riferimento formato da due rette perpendicolari, l'asse delle ascisse (x) e l'asse delle ordinate (y). Ogni punto nel piano è identificato da una coppia di coordinate (x, y). Pensa al piano cartesiano come una griglia che ci permette di localizzare qualsiasi punto con precisione.
Retta: Una retta è un insieme infinito di punti allineati. Nel piano cartesiano, una retta può essere rappresentata graficamente e algebricamente.
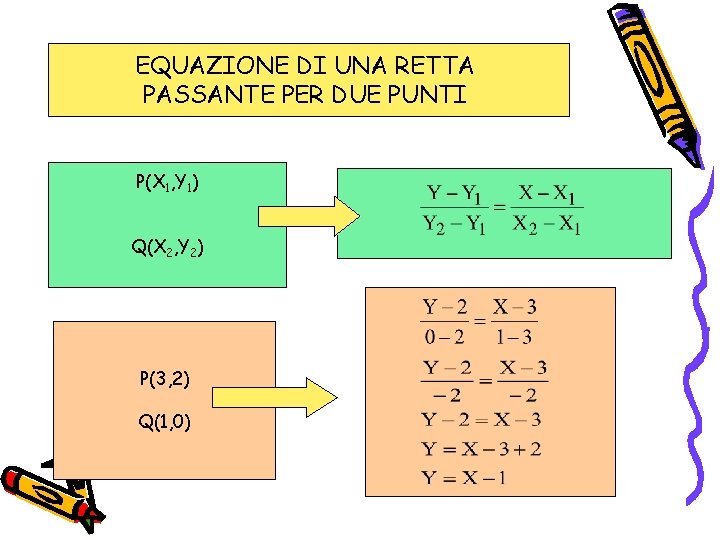
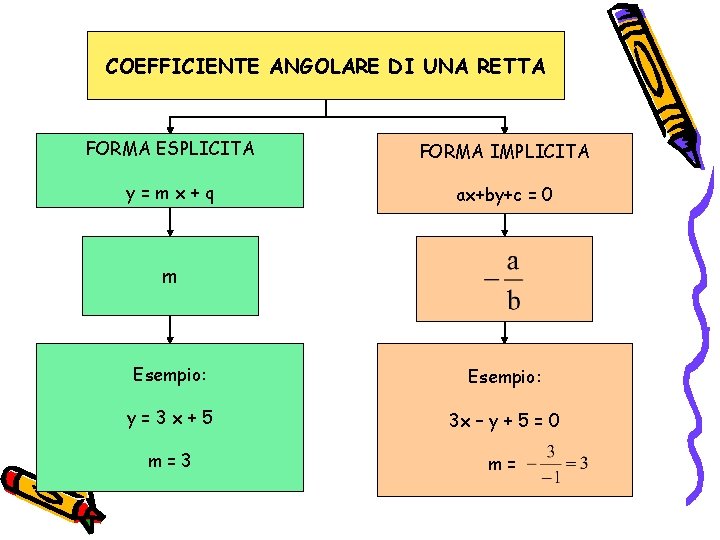
Equazione della Retta: L'equazione della retta è la formula che descrive la relazione tra le coordinate x e y di tutti i punti che appartengono alla retta. Esistono diverse forme di equazione, ma la più comune è la forma esplicita: y = mx + q.
Forma Esplicita (y = mx + q):
- m (Coefficiente Angolare): Indica la pendenza della retta, cioè quanto la retta sale o scende per ogni unità di spostamento orizzontale. Un valore positivo di m indica una retta crescente, un valore negativo indica una retta decrescente, e m=0 indica una retta orizzontale. Immagina di scalare una montagna: il coefficiente angolare è come l'inclinazione del sentiero.
- q (Termine Noto): Indica l'ordinata all'origine, cioè il punto in cui la retta interseca l'asse delle ordinate (y). È il valore di y quando x = 0. Pensa al termine noto come l'altezza di partenza quando inizi a scalare la montagna.
Forma Implicita (ax + by + c = 0): Un'altra forma di equazione della retta è la forma implicita. Anche se meno intuitiva della forma esplicita, è utile per rappresentare tutte le rette, comprese quelle verticali che non possono essere espresse nella forma y = mx + q.
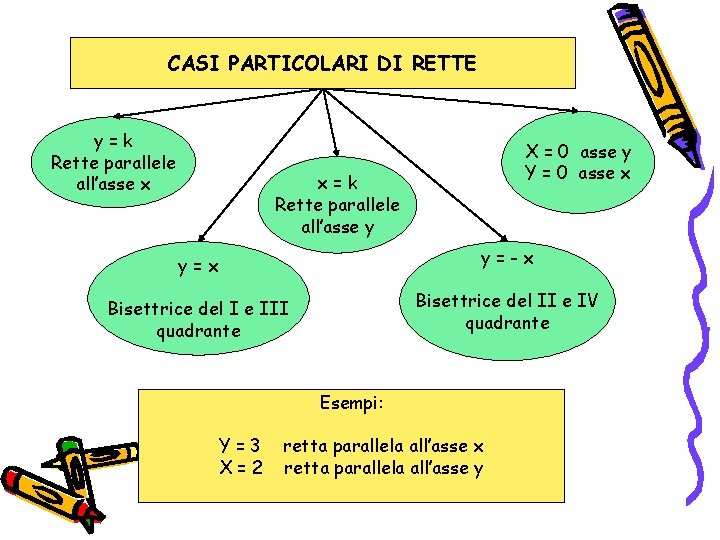
Retta Verticale: Una retta verticale ha equazione x = k, dove k è una costante. La sua pendenza è indefinita (o infinita).
Retta Orizzontale: Una retta orizzontale ha equazione y = k, dove k è una costante. La sua pendenza è zero.
Parallelismo: Due rette sono parallele se hanno lo stesso coefficiente angolare (m1 = m2). Immagina due sentieri di montagna che hanno la stessa pendenza e quindi non si incontrano mai.
Perpendicolarità: Due rette sono perpendicolari se il prodotto dei loro coefficienti angolari è -1 (m1 * m2 = -1). Immagina due sentieri che si incrociano formando un angolo retto.
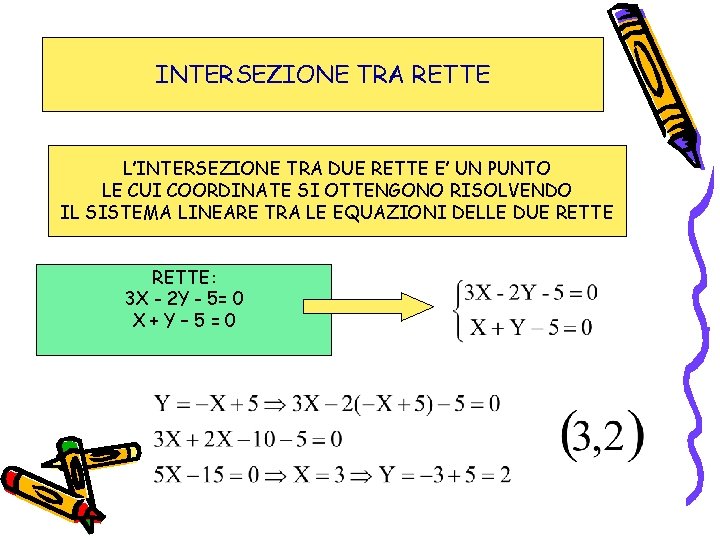
Intersezione tra Rette: Il punto di intersezione tra due rette è la soluzione del sistema di equazioni formato dalle equazioni delle due rette. È il punto in cui i due sentieri si incontrano.

Applicazioni Pratiche: La Retta nel Mondo Reale

Come promesso, torniamo al mondo reale. La retta non è solo un concetto teorico, ma ha numerose applicazioni pratiche:

Fisica: La retta è utilizzata per descrivere il moto uniforme di un corpo, la relazione tra forza e accelerazione, e molti altri fenomeni fisici.
Economia: La retta è utilizzata per rappresentare le curve di domanda e offerta, le funzioni di costo e ricavo, e per analizzare l'andamento dei mercati.
Informatica: La retta è utilizzata nella grafica computerizzata, nella modellazione 3D, e nella programmazione di algoritmi.
Statistica: La retta di regressione lineare viene utilizzata per modellare la relazione tra due variabili statistiche.

Obiezioni Comuni e Come Superarle

Alcune persone potrebbero obiettare che la geometria analitica è troppo astratta e poco utile nella vita di tutti i giorni. Altri potrebbero sostenere che esistono approcci più semplici per risolvere i problemi. È vero, esistono alternative, ma la geometria analitica fornisce un quadro completo e rigoroso, che permette di comprendere a fondo i concetti e di applicarli in contesti diversi. Inoltre, la capacità di pensare in modo analitico è una competenza preziosa in molti campi, non solo nella matematica.

Un'altra obiezione comune è la difficoltà nel memorizzare le formule. Ma l'obiettivo non è memorizzare a memoria, ma capire il significato delle formule e come utilizzarle. La mappa concettuale è uno strumento che ti aiuta proprio in questo, a collegare i concetti e a ricordare le formule in modo intuitivo.

Soluzioni e Consigli Pratici

Ecco alcuni consigli pratici per affrontare lo studio della retta nel piano cartesiano:

Parti dalle basi: Assicurati di aver compreso bene i concetti fondamentali del piano cartesiano e delle coordinate.
Utilizza la mappa concettuale: Crea la tua mappa concettuale, personalizzandola con i tuoi esempi e i tuoi schemi.
Fai tanti esercizi: La pratica è fondamentale per acquisire sicurezza e familiarità con le formule.
Non aver paura di chiedere aiuto: Se hai difficoltà, non esitare a chiedere spiegazioni al tuo insegnante, ai tuoi compagni di classe, o a cercare risorse online.
Utilizza software di geometria dinamica: Software come GeoGebra ti permettono di visualizzare le rette, di modificarne i parametri e di osservare l'effetto delle modifiche in tempo reale.
Collega la teoria alla pratica: Cerca esempi concreti di applicazioni della retta nel mondo reale.
Sii paziente: La comprensione richiede tempo e impegno. Non scoraggiarti di fronte alle difficoltà, ma persevera e vedrai i risultati.

Ricorda, l'obiettivo non è diventare un matematico provetto, ma acquisire una competenza utile per affrontare le sfide del mondo di oggi. La capacità di analizzare, di ragionare in modo logico, e di risolvere problemi è una competenza preziosa in qualsiasi campo tu voglia intraprendere.

In conclusione, la mappa concettuale sulla retta nel piano cartesiano è uno strumento potente che ti aiuta a organizzare le informazioni, a collegare i concetti e a superare le difficoltà. Non è una bacchetta magica, ma un aiuto concreto per affrontare un argomento che, a prima vista, può sembrare complicato. Utilizzala, sperimenta, e scopri il piacere di capire la matematica!

Adesso, prova a rispondere a questa domanda: In che modo la comprensione della retta nel piano cartesiano potrebbe aiutarti a risolvere un problema concreto nella tua vita o nel tuo campo di studi?