Logaritmo In Base 2 Di 1

Ti sei mai chiesto come i computer, che parlano solo con 0 e 1, riescono a fare calcoli complessi, gestire immagini, riprodurre musica e persino prevedere il tempo? La risposta, in parte, risiede in un concetto matematico fondamentale: il logaritmo. E oggi ci concentreremo su un caso particolare, ma cruciale: il logaritmo in base 2 di 1, o, per dirla in termini più semplici, log₂(1).

Magari stai studiando per un esame di matematica, oppure sei semplicemente curioso di capire meglio come funzionano le cose a livello più profondo. Qualunque sia la tua motivazione, questo articolo è pensato per te. Cercheremo di rendere il concetto il più chiaro possibile, senza usare gergo matematico complicato e offrendo esempi pratici per aiutarti a visualizzare meglio.

Cosa significa "Logaritmo"?

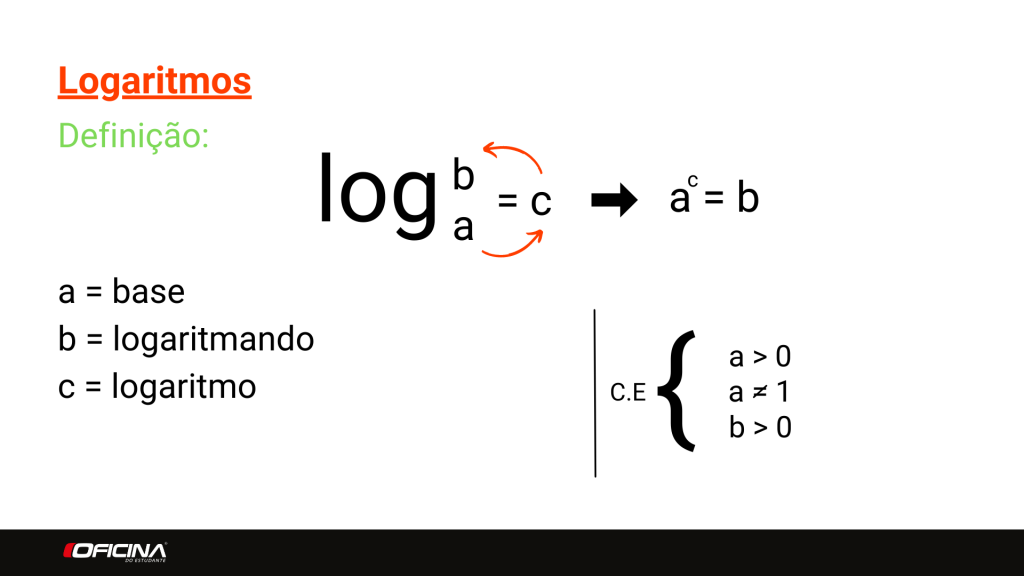
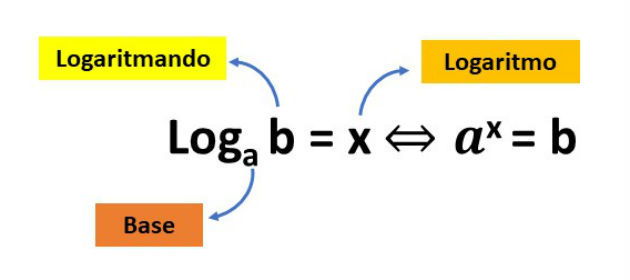
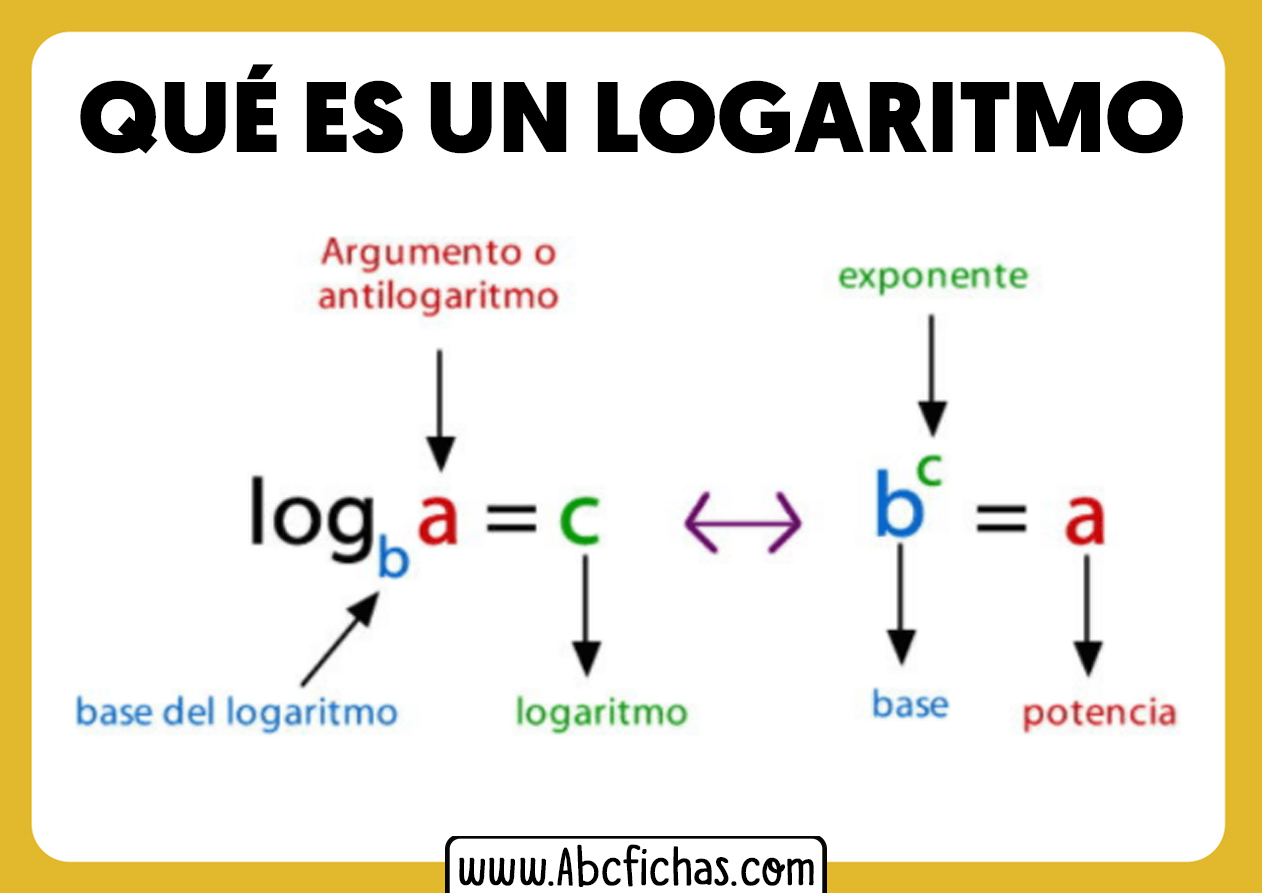
Prima di addentrarci nel log₂(1), cerchiamo di capire cos'è un logaritmo in generale. Immagina di avere un numero (chiamiamolo "base") e di voler sapere a quale potenza devi elevarlo per ottenere un altro numero (chiamiamolo "argomento"). Il logaritmo è proprio l'esponente che stai cercando.

In termini matematici: se b^x = y, allora log_b(y) = x. Qui, 'b' è la base, 'x' è l'esponente (il logaritmo) e 'y' è l'argomento.

Facciamo un esempio semplice: 2³ = 8. Quindi, il logaritmo in base 2 di 8 è 3, cioè log₂(8) = 3.

Il Logaritmo in Base 2: Un'Importante Premessa

Il logaritmo in base 2, spesso chiamato anche logaritmo binario, è particolarmente importante in informatica e nelle discipline correlate. Questo perché i computer funzionano con il sistema binario, che utilizza solo due cifre: 0 e 1. Ogni dato, istruzione o operazione viene alla fine rappresentata come una sequenza di bit (binary digits).

Quindi, quando si parla di quanti bit sono necessari per rappresentare un certo numero di informazioni, o di quante divisioni successive per 2 sono necessarie per risolvere un problema (come nella ricerca binaria), il logaritmo in base 2 entra in gioco.

Calcoliamo log₂(1)

Ora che abbiamo le basi, possiamo affrontare il nostro problema: trovare il logaritmo in base 2 di 1. Ricorda la definizione: log_b(y) = x significa che b^x = y.

Nel nostro caso, dobbiamo trovare 'x' tale che 2^x = 1.

Quale numero, elevato a potenza, dà come risultato 1? La risposta è 0. Qualsiasi numero (eccetto 0) elevato alla potenza 0 è uguale a 1. Pertanto: 2⁰ = 1.

Quindi, log₂(1) = 0.

Potrebbe sembrare un risultato banale, ma è fondamentale per capire come funzionano alcuni algoritmi e sistemi informatici.

Perché log₂(1) = 0 è importante?

Ecco alcuni esempi di come questo concetto apparentemente semplice si manifesta nel mondo reale:

* Alberi binari: Negli alberi binari, una struttura dati fondamentale in informatica, il numero di nodi al livello 0 è sempre 1 (la radice). Il logaritmo in base 2 ci aiuta a capire l'altezza di un albero binario completo e quindi a stimare la complessità degli algoritmi che lo attraversano. * Ricerca binaria: La ricerca binaria è un algoritmo efficiente per trovare un elemento in un elenco ordinato. Ad ogni passaggio, l'elenco viene diviso a metà. Il numero di passaggi necessari per trovare un elemento è legato al logaritmo in base 2 della dimensione dell'elenco. Se l'elemento cercato è il primo, l'algoritmo lo troverà immediatamente, richiedendo 0 passaggi in più (quasi un'analogia con log₂(1) = 0). * Teoria dell'informazione: In teoria dell'informazione, il logaritmo in base 2 viene utilizzato per misurare la quantità di informazione contenuta in un messaggio. Un evento certo (probabilità = 1) non porta alcuna nuova informazione. Il logaritmo (in base 2) di 1, che è 0, riflette questa idea. * Complessità algoritmica: Spesso, la complessità di un algoritmo viene espressa in termini di notazione O-grande. Quando un algoritmo ha una complessità di O(1), significa che il tempo di esecuzione è costante, indipendente dalla dimensione dell'input. La ricerca di un elemento in un array se conosciamo già la sua posizione è un esempio, e può essere collegata concettualmente al fatto che log₂(1) = 0 indica un'operazione immediata.

Esempi pratici per visualizzare il concetto

Immagina di dover trovare un ago in un pagliaio. Ecco due scenari:

Scenario 1: Il pagliaio è vuoto. Non c'è niente da cercare! In questo caso, non devi fare nulla. Questo corrisponde a log₂(1) = 0. Non ci sono "divisioni" o passaggi necessari perché non c'è niente da dividere o cercare.
Scenario 2: Il pagliaio è pieno di paglia, ma sai già che l'ago è esattamente in un punto specifico. Anche in questo caso, la ricerca è immediata. Non hai bisogno di dividere il pagliaio o di fare congetture. Ancora una volta, log₂(1) = 0.

Questi esempi, sebbene semplificati, ti aiutano a visualizzare come il logaritmo in base 2 di 1 possa rappresentare una situazione in cui non è necessaria alcuna operazione o calcolo.

Conclusione

Anche se può sembrare un concetto astratto, log₂(1) = 0 è un tassello importante del puzzle che compone la matematica e l'informatica. Comprendere il significato di questo risultato ti permette di apprezzare meglio come i computer gestiscono le informazioni e risolvono i problemi.

Spero che questo articolo ti abbia aiutato a demistificare il concetto di logaritmo in base 2 di 1. Ricorda, la matematica non è un insieme di formule da memorizzare, ma uno strumento potente per comprendere il mondo che ci circonda.

Non aver paura di esplorare ulteriormente questi concetti! La tua curiosità è la chiave per sbloccare nuove conoscenze.

Continua a imparare e a sperimentare!