Lo Spazio Di Frenatura E Indipendente Dalla Velocita

L'idea che lo spazio di frenatura di un veicolo sia indipendente dalla sua velocità iniziale è un concetto che, a prima vista, può sembrare controintuitivo. La nostra esperienza quotidiana ci suggerisce che più velocemente andiamo, più spazio ci serve per fermarci. Tuttavia, approfondendo le leggi della fisica che governano la frenata, scopriremo che in realtà esiste una componente dello spazio di arresto, quella legata esclusivamente alla decelerazione, che può essere analizzata come potenzialmente indipendente dalla velocità iniziale, sotto specifiche e ideali condizioni.

Frenata e Decelerazione: Una Distinzione Fondamentale

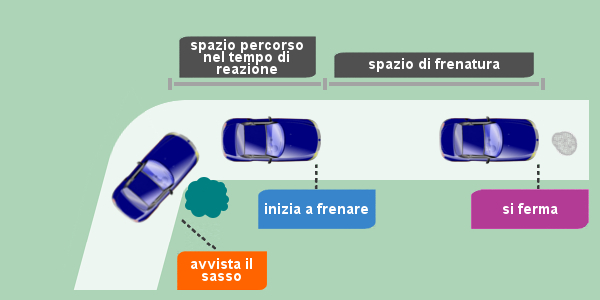
È cruciale distinguere tra lo spazio di arresto totale e lo spazio di frenatura puro. Lo spazio di arresto totale include il tempo di reazione del conducente, il tempo necessario al sistema frenante per attivarsi e, infine, lo spazio percorso durante la fase di decelerazione. Lo spazio di frenatura puro, invece, considera solo lo spazio percorso durante la decelerazione effettiva, una volta che i freni sono completamente attivati.

Le Leggi della Fisica in Gioco

La fisica ci dice che la forza di attrito, responsabile della decelerazione, è proporzionale alla forza normale (la forza con cui il veicolo preme sulla superficie stradale) e al coefficiente di attrito tra i pneumatici e l'asfalto. La formula fondamentale è:

F = μ * N

Dove:

• F è la forza di attrito.
• μ è il coefficiente di attrito.
• N è la forza normale.

Se assumiamo che il coefficiente di attrito (μ) rimanga costante (cosa non sempre vera nella realtà, ma utile per un'analisi teorica) e che la forza normale (N) non vari significativamente (situazione valida su una superficie piana), allora la forza di decelerazione (F) è anch'essa costante. Questo significa che il veicolo decelera con un'accelerazione negativa costante.

La Cinematica della Decelerazione Costante

In cinematica, l'equazione che descrive lo spazio percorso da un oggetto con accelerazione costante è:

Δx = v₀ * t + (1/2) * a * t²

Dove:

• Δx è lo spazio percorso.
• v₀ è la velocità iniziale.
• t è il tempo.
• a è l'accelerazione (in questo caso negativa, quindi decelerazione).

Per trovare lo spazio di frenatura (Δx) puro, dobbiamo considerare il tempo necessario per arrestare il veicolo (vf = 0). Usando l'equazione:

vf = v₀ + a * t

Possiamo ricavare il tempo di frenatura (t):

t = -v₀ / a

Sostituendo questo valore di 't' nell'equazione dello spazio percorso, otteniamo:

Δx = v₀ * (-v₀ / a) + (1/2) * a * (-v₀ / a)²

Semplificando:

Δx = -v₀² / a + (1/2) * v₀² / a

Δx = - (1/2) * v₀² / a

Questo mostra che lo spazio di frenatura (Δx) è proporzionale al quadrato della velocità iniziale (v₀²) e inversamente proporzionale all'accelerazione (a). Quindi, se l'accelerazione (decelerazione) fosse indipendente dalla velocità iniziale, allora lo spazio di frenatura puro sarebbe legato alla velocità iniziale in modo quadratico, e non lineare, come intuitivamente si potrebbe pensare.

Condizioni Ideali e Realtà

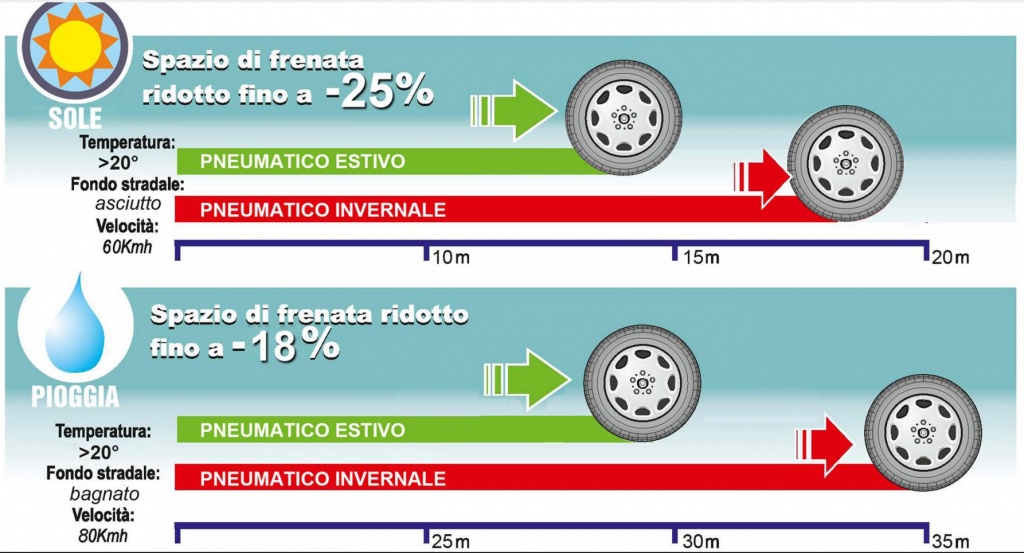
L'analisi precedente si basa su condizioni ideali che raramente si verificano nella realtà. Il coefficiente di attrito (μ) non è costante. Varia in base a diversi fattori, tra cui:

• Condizioni della strada: asciutta, bagnata, ghiacciata, innevata.
• Tipo di pneumatico: mescola, pressione, usura.
• Temperatura: influenza le proprietà dei pneumatici e dell'asfalto.

Inoltre, i sistemi di frenata moderni, come l'ABS (Anti-lock Braking System), modulano la forza frenante per evitare il bloccaggio delle ruote, massimizzando l'aderenza e, di conseguenza, l'accelerazione negativa. L'ABS lavora per mantenere il pneumatico al punto di massima aderenza, ottimizzando la decelerazione. La presenza dell'ABS rende l'accelerazione di frenata *meno dipendente* dalle abilità del guidatore, ma non la rende magicamente indipendente dalla velocità.

Un altro fattore da considerare è la resistenza aerodinamica, che aumenta con la velocità. A velocità elevate, la resistenza dell'aria contribuisce significativamente alla decelerazione. Tuttavia, a basse velocità, il suo impatto è trascurabile.

Esempi e Dati nel Mondo Reale

Numerosi test e ricerche nel settore automobilistico dimostrano che lo spazio di frenatura aumenta con la velocità. Ad esempio:

• Un'auto che viaggia a 50 km/h potrebbe richiedere circa 15 metri per fermarsi su asfalto asciutto.
• La stessa auto a 100 km/h potrebbe aver bisogno di 50-60 metri.
• Su asfalto bagnato, lo spazio di frenatura può aumentare significativamente, anche del 50-100%.

Questi dati evidenziano che lo spazio di frenatura non è indipendente dalla velocità. Piuttosto, aumenta in modo più che proporzionale all'aumentare della velocità. La relazione è più complessa di una semplice proporzionalità lineare a causa dei fattori menzionati in precedenza (coefficiente di attrito variabile, ABS, resistenza aerodinamica).

Tuttavia, è importante notare che *se* potessimo mantenere costante l'accelerazione di frenata, lo spazio di arresto aggiuntivo necessario per ogni incremento di velocità sarebbe via via minore. Questo perché, per esempio, passare da 90km/h a 100km/h richiederebbe meno spazio aggiuntivo che passare da 10km/h a 20km/h, *sempre se* la decelerazione fosse identica in entrambi i casi.

Conclusioni

L'affermazione che lo spazio di frenatura sia indipendente dalla velocità è errata nella pratica quotidiana. La nostra analisi teorica, basata su condizioni ideali, ci ha permesso di isolare la relazione tra spazio di frenatura puro e velocità, mostrando una dipendenza quadratica. Tuttavia, nella realtà, il coefficiente di attrito variabile, i sistemi ABS e altri fattori rendono la situazione molto più complessa. Lo spazio di arresto aumenta significativamente con la velocità, rendendo fondamentale mantenere distanze di sicurezza adeguate e adattare la guida alle condizioni stradali.

Ricorda sempre: una guida prudente e responsabile è la chiave per la sicurezza stradale. Rallenta, rispetta le distanze di sicurezza e guida in modo consapevole! Informarsi e comprendere i principi fisici alla base della frenata può aiutarti a prendere decisioni migliori al volante e a ridurre il rischio di incidenti.